
Permutation polynomial
Encyclopedia
In mathematics
, a permutation polynomial (for a given finite ring
) is a polynomial
that acts as a permutation
of the elements of the ring, i.e. the map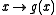 is one-to-one. In case the ring is a finite field
is one-to-one. In case the ring is a finite field
, they are (under certain assumptions) essentially Dickson polynomials which are closely related to the Chebyshev polynomials
.
In the case of finite rings Z/nZ, such polynomials have also been studied and applied in the interleaver component of error detection and correction
algorithms.
permutation polynomials. Actually it is possible if and only if n is divisible by p2 for some prime number p.
The construction is surprisingly simple, nevertheless it can produce permutations with certain good properties. That is why it has been used in the interleaver component of turbo codes in 3GPP Long Term Evolution
mobile telecommunication standard (see 3GPP technical specification 36.212 e.g. page 14 in version 8.8.0).
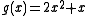 for the ring Z/4Z.
for the ring Z/4Z.
One sees: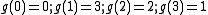 ,
,
so the polynomial defines the permutation
One sees: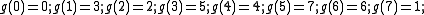 ,
,
so the polynomial defines the permutation
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a permutation polynomial (for a given finite ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
) is a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
that acts as a permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of the elements of the ring, i.e. the map
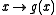 is one-to-one. In case the ring is a finite field
is one-to-one. In case the ring is a finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
, they are (under certain assumptions) essentially Dickson polynomials which are closely related to the Chebyshev polynomials
Chebyshev polynomials
In mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
.
In the case of finite rings Z/nZ, such polynomials have also been studied and applied in the interleaver component of error detection and correction
Error detection and correction
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction or error control are techniques that enable reliable delivery of digital data over unreliable communication channels...
algorithms.
Quadratic permutation polynomials (QPP)
For the finite ring Z/nZ one can construct quadraticpermutation polynomials. Actually it is possible if and only if n is divisible by p2 for some prime number p.
The construction is surprisingly simple, nevertheless it can produce permutations with certain good properties. That is why it has been used in the interleaver component of turbo codes in 3GPP Long Term Evolution
3GPP Long Term Evolution
3GPP Long Term Evolution, usually referred to as LTE, is a standard for wireless communication of high-speed data for mobile phones and data terminals. It is based on the GSM/EDGE and UMTS/HSPA network technologies, increasing the capacity and speed using new modulation techniques...
mobile telecommunication standard (see 3GPP technical specification 36.212 e.g. page 14 in version 8.8.0).
Simple examples
Consider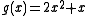 for the ring Z/4Z.
for the ring Z/4Z.One sees:
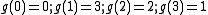 ,
,so the polynomial defines the permutation
-
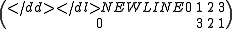 .
.
Let us consider the same polynomial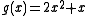 for the other ring
for the other ring
One sees:
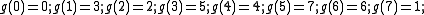 ,
,so the polynomial defines the permutation
-
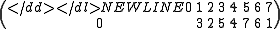 .
.
Rings Z/pkZ
Consider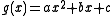 for the ring Z/pkZ.
for the ring Z/pkZ.
Lemma: for k=1 (i.e. Z/pZ) such polynomial defines a permutation
only in the case a=0 and b not equal to zero. So the polynomial is not quadratic, but linear.
Lemma: for k>1 ( Z/pkZ) such polynomial defines a permutation if and only if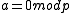 and
and 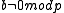 .
.
Rings Z/
nZ Consider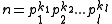 , where pt are prime numbers.
, where pt are prime numbers.
Lemma: any polynomial
defines a permutation for the ring Z/nZ if and only if all the polynomials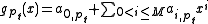 defines the permutations for all rings
defines the permutations for all rings 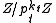 , where
, where
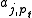 are remainders of
are remainders of 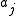
modula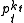 .
.
As a corollary one can construct plenty quadratic permutation polynomials using the following simple construction.
Consider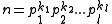 , assume that k1 >1.
, assume that k1 >1.
Consider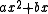 , such that
, such that 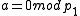 , but
, but  ; assume that
; assume that 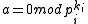 ,i>1. And assume that
,i>1. And assume that 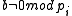 for all i=1...l.
for all i=1...l.
(For example one can take
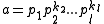
and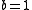 ).
).
Then such polynomial defines a permutation.
To see this we observe that for all primes pi,i>1, the reduction of this quadratic polynomial modula pi is actually linear polynomial and hence is permutation by trivial reason. For the first prime number we should use
the lemma discussed previously to see that it defines the permutation.
For example, consider Z/12Z and polynomial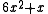 .
.
It defines a permutation
-
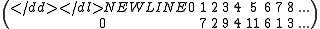 .
.
Higher degree polynomials
Consider polynomial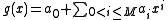 for the ring
for the ring
Lemma: if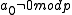 and
and  i>0, then polynomial g(x) defines a permutation for the elements of the ring Z/pkZ for k>1.
i>0, then polynomial g(x) defines a permutation for the elements of the ring Z/pkZ for k>1.
However contrary to the case of the quadratic polynomials the lemma is not if and only if. This can be seen from the following statement.
Lemma: consider finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
Z/pZ for some prime number p.
The cubic polynomial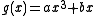 defines a permutation if and only if for all
defines a permutation if and only if for all 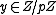 it is true that
it is true that 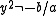 , i.e. the Legendre symbolLegendre symbolIn number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
, i.e. the Legendre symbolLegendre symbolIn number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
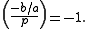 .
.
Evaluation of the Legendre symbolLegendre symbolIn number theory, the Legendre symbol is a multiplicative function with values 1, −1, 0 that is a quadratic character modulo a prime number p: its value on a quadratic residue mod p is 1 and on a quadratic non-residue is −1....
can be achieved with the help of quadratic reciprocity law.
So one can see that the analysis of higher degree polynomials to define a permutation is quite subtle question. -

