Perplexity
Encyclopedia
Perplexity is a measurement in information theory
. It is defined as b raised to the power of entropy
in base b, or more often as b raised to the power of cross-entropy in base b. The latter definition is commonly used to compare probability models.
p is defined as
where H(p) is the entropy of the distribution and x ranges over events.
One may also define the perplexity of a random variable
X
as the perplexity of the distribution over its possible values x.
It is easy to see that in the special case where p models a fair k-sided die (a uniform distribution over k discrete events), its perplexity is k. We may therefore regard any random variable with perplexity k as having the same uncertainty as a fair k-sided die. We are "k-ways perplexed" about the value of such a random variable. (Unless it is also a fair k-sided die, more than k values will be possible, but the overall uncertainty is no greater because some of these values will have probability greater than 1/k.)
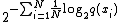
Better models q of the unknown distribution p will tend to assign higher probabilities q(xi) to the test events. Thus, they have lower perplexity: they are less surprised by the test sample.
The exponent above may be regarded as the average number of bits needed to represent a test event xi if one uses an optimal code based on q. Low-perplexity models do a better job of compressing the test sample, requiring few bits per test element on average because q(xi) tends to be high.
The exponent may also be regarded as a cross-entropy,
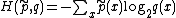
where
denotes the empirical distribution of the test sample (i.e., 
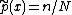if x appeared n times in the test sample of size N).
, perplexity is a common way of evaluating language model
s. A language model is a probability distribution over entire sentences or texts.
Using the definition above, one might find that the average sentence xi in the test sample could be coded in 190 bits (i.e., the test sentences had an average log-probability of -190). This would give an enormous model perplexity of 2190 per sentence. However, it is more common to normalize for sentence length and consider only the number of bits per word. Thus, if the test sample's sentences comprised a total of 1,000 words, and could be coded using a total of 7,950 bits, one could report a model perplexity of 27.95 = 247 per word. In other words, the model is as confused on test data as if it had to choose uniformly and independently among 247 possibilities for each word.
The lowest perplexity that has been published on the Brown Corpus
(1 million words of American English
of varying topics and genres) as of 1992 is indeed about 247 per word, corresponding to a cross-entropy of log2247 = 7.95 bits per word or 1.75 bits per letter using a trigram
model. It is often possible to achieve lower perplexity on more specialized corpora
, as they are more predictable.
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
. It is defined as b raised to the power of entropy
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
in base b, or more often as b raised to the power of cross-entropy in base b. The latter definition is commonly used to compare probability models.
Perplexity of a probability distribution
The perplexity of a discrete probability distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
p is defined as
where H(p) is the entropy of the distribution and x ranges over events.
One may also define the perplexity of a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X
as the perplexity of the distribution over its possible values x.
It is easy to see that in the special case where p models a fair k-sided die (a uniform distribution over k discrete events), its perplexity is k. We may therefore regard any random variable with perplexity k as having the same uncertainty as a fair k-sided die. We are "k-ways perplexed" about the value of such a random variable. (Unless it is also a fair k-sided die, more than k values will be possible, but the overall uncertainty is no greater because some of these values will have probability greater than 1/k.)
Perplexity of a probability model
Often one tries to model an unknown probability distribution p, based on a training sample that was drawn from p. Given a proposed probability model q, one may evaluate q by asking how well it predicts a separate test sample x1, x2, ..., xN also drawn from p. The perplexity of the model q is defined as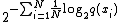Better models q of the unknown distribution p will tend to assign higher probabilities q(xi) to the test events. Thus, they have lower perplexity: they are less surprised by the test sample.
The exponent above may be regarded as the average number of bits needed to represent a test event xi if one uses an optimal code based on q. Low-perplexity models do a better job of compressing the test sample, requiring few bits per test element on average because q(xi) tends to be high.
The exponent may also be regarded as a cross-entropy,
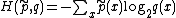
where
denotes the empirical distribution of the test sample (i.e., 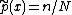if x appeared n times in the test sample of size N).Perplexity per word
In natural language processingNatural language processing
Natural language processing is a field of computer science and linguistics concerned with the interactions between computers and human languages; it began as a branch of artificial intelligence....
, perplexity is a common way of evaluating language model
Language model
A statistical language model assigns a probability to a sequence of m words P by means of a probability distribution.Language modeling is used in many natural language processing applications such as speech recognition, machine translation, part-of-speech tagging, parsing and information...
s. A language model is a probability distribution over entire sentences or texts.
Using the definition above, one might find that the average sentence xi in the test sample could be coded in 190 bits (i.e., the test sentences had an average log-probability of -190). This would give an enormous model perplexity of 2190 per sentence. However, it is more common to normalize for sentence length and consider only the number of bits per word. Thus, if the test sample's sentences comprised a total of 1,000 words, and could be coded using a total of 7,950 bits, one could report a model perplexity of 27.95 = 247 per word. In other words, the model is as confused on test data as if it had to choose uniformly and independently among 247 possibilities for each word.
The lowest perplexity that has been published on the Brown Corpus
Brown Corpus
The Brown University Standard Corpus of Present-Day American English was compiled in the 1960s by Henry Kucera and W. Nelson Francis at Brown University, Providence, Rhode Island as a general corpus in the field of corpus linguistics...
(1 million words of American English
English language
English is a West Germanic language that arose in the Anglo-Saxon kingdoms of England and spread into what was to become south-east Scotland under the influence of the Anglian medieval kingdom of Northumbria...
of varying topics and genres) as of 1992 is indeed about 247 per word, corresponding to a cross-entropy of log2247 = 7.95 bits per word or 1.75 bits per letter using a trigram
N-gram
In the fields of computational linguistics and probability, an n-gram is a contiguous sequence of n items from a given sequence of text or speech. The items in question can be phonemes, syllables, letters, words or base pairs according to the application...
model. It is often possible to achieve lower perplexity on more specialized corpora
Text corpus
In linguistics, a corpus or text corpus is a large and structured set of texts...
, as they are more predictable.