Phase correlation
Encyclopedia
In image processing
, phase correlation is a method of image registration
, and uses a fast frequency-domain approach to estimate the relative translative
offset between two similar image
s.
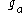and 
:
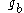Apply a window function
(e.g., a Hamming window) on both images to reduce edge effects. Then, calculate the discrete 2D Fourier transform
of both images.
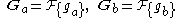
Calculate the cross-power spectrum by taking the complex conjugate
of the second result, multiplying the Fourier transform
s together elementwise, and normalizing this product elementwise.
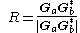
Obtain the normalized cross-correlation by applying the inverse Fourier transform.
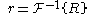
Determine the location of the peak in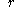
(possibly using sub-pixel edge detection).
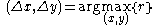
Let the two images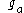
and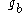 
be circularly-shifted versions of each other:
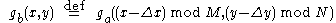
(where the images are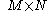
in size).
Then, the discrete Fourier transforms of the images will be shifted relatively in phase
:
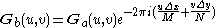
One can then calculate the normalized cross-power spectrum to factor out the phase difference:
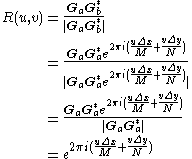
since the magnitude of a complex exponential
always is one, and the phase of
always is zero.
The inverse Fourier transform of a complex exponential is a Kronecker delta, i.e. a single peak:
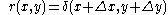
This result could have been obtained by calculating the cross correlation directly. The advantage of this method is that the discrete Fourier transform and its inverse can be performed using the fast Fourier transform
, which is much faster than correlation for large images.
The method can be extended to determine rotation and scaling differences between two images by first converting the images to log-polar coordinates. Due to properties of the Fourier transform
, the rotation and scaling parameters can be determined in a manner invariant to translation.
will be a simple linear shift of 
, rather than a circular shift as required by the explanation above. In such cases,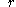 
will not be a simple delta function, which will reduce the performance of the method. In such cases, a window function
should be employed during the Fourier transform to reduce edge effects, or the images should be zero padded so that the edge effects can be ignored. If the images consist of a flat background, with all detail situated away from the edges, then a linear shift will be equivalent to a circular shift, and the above derivation will hold exactly.
For periodic
images (such as a chessboard), phase correlation may yield ambiguous results with several peaks in the resulting output.
, as it leaves the fewest artifacts.
Television
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
, phase correlation is a method of image registration
Image registration
Image registration is the process of transforming different sets of data into one coordinate system. Data may be multiple photographs, data from different sensors, from different times, or from different viewpoints. It is used in computer vision, medical imaging, military automatic target...
, and uses a fast frequency-domain approach to estimate the relative translative
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
offset between two similar image
Image
An image is an artifact, for example a two-dimensional picture, that has a similar appearance to some subject—usually a physical object or a person.-Characteristics:...
s.
Example
The following image demonstrates the usage of phase correlation to determine relative translative movement between two images corrupted by independent Gaussian noise. The image was translated by (30,33) pixels. Accordingly, one can clearly see a peak in the phase-correlation representation at approximately (30,33).Method
Given two input images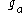 and 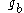:Apply a window function
Window function
In signal processing, a window function is a mathematical function that is zero-valued outside of some chosen interval. For instance, a function that is constant inside the interval and zero elsewhere is called a rectangular window, which describes the shape of its graphical representation...
(e.g., a Hamming window) on both images to reduce edge effects. Then, calculate the discrete 2D Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
of both images.
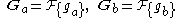
Calculate the cross-power spectrum by taking the complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
of the second result, multiplying the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
s together elementwise, and normalizing this product elementwise.
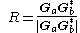
Obtain the normalized cross-correlation by applying the inverse Fourier transform.
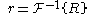
Determine the location of the peak in
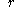(possibly using sub-pixel edge detection).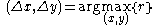Rationale
The method is based on the Fourier shift theorem.Let the two images
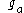and 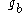be circularly-shifted versions of each other: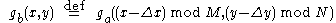(where the images are
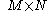in size).Then, the discrete Fourier transforms of the images will be shifted relatively in phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
:
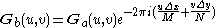
One can then calculate the normalized cross-power spectrum to factor out the phase difference:
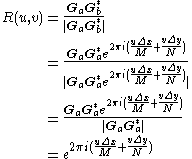
since the magnitude of a complex exponential
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
always is one, and the phase of
always is zero.The inverse Fourier transform of a complex exponential is a Kronecker delta, i.e. a single peak:
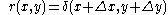
This result could have been obtained by calculating the cross correlation directly. The advantage of this method is that the discrete Fourier transform and its inverse can be performed using the fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
, which is much faster than correlation for large images.
Benefits
Unlike many spatial-domain algorithms, the phase correlation method is resilient to noise, occlusions, and other defects typical of medical or satellite images.The method can be extended to determine rotation and scaling differences between two images by first converting the images to log-polar coordinates. Due to properties of the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
, the rotation and scaling parameters can be determined in a manner invariant to translation.
Limitations
In practice, it is more likely that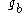 will be a simple linear shift of 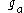, rather than a circular shift as required by the explanation above. In such cases, 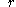will not be a simple delta function, which will reduce the performance of the method. In such cases, a window functionWindow function
In signal processing, a window function is a mathematical function that is zero-valued outside of some chosen interval. For instance, a function that is constant inside the interval and zero elsewhere is called a rectangular window, which describes the shape of its graphical representation...
should be employed during the Fourier transform to reduce edge effects, or the images should be zero padded so that the edge effects can be ignored. If the images consist of a flat background, with all detail situated away from the edges, then a linear shift will be equivalent to a circular shift, and the above derivation will hold exactly.
For periodic
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
images (such as a chessboard), phase correlation may yield ambiguous results with several peaks in the resulting output.
Applications
Phase correlation is the preferred method for television standards conversionTelevision standards conversion
Television standards conversion is the process of changing one type of TV system to another. The most common is from NTSC to PAL or the other way around. This is done so TV programs in one nation may be viewed in a nation with a different standard...
, as it leaves the fewest artifacts.
See also
General- Cross correlation
Television
- Television standards conversionTelevision standards conversionTelevision standards conversion is the process of changing one type of TV system to another. The most common is from NTSC to PAL or the other way around. This is done so TV programs in one nation may be viewed in a nation with a different standard...
- Reverse Standards ConversionReverse Standards ConversionReverse Standards Conversion or RSC is a process developed by a team led by James Insell at the BBC for the restoration of video recordings which have already been converted between different video standards using early conversion techniques....