Pierpont prime
Encyclopedia
A Pierpont prime is a prime number
of the form
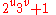
for some nonnegative integer
s u and v. They are named after the mathematician James Pierpont
.
It is possible to prove that if v = 0 and u > 0, then u must be a power of 2, making the prime a Fermat prime. If v is positive then u must also be positive, and the Pierpont prime is of the form 6k + 1 (because if u = 0 and v > 0 then 2u3v + 1 is an even number greater than 2 and therefore composite).
The first few Pierpont primes are:
 Andrew Gleason
Andrew Gleason
conjectured there are infinitely many Pierpont primes. They are not particularly rare and there are few restrictions from algebraic factorisations, so there are no requirements like the Mersenne prime
condition that the exponent must be prime. There are 36 Pierpont primes less than 106, 59 less than 109, 151 less than 1020, and 789 less than 10100; conjecturally there are O(log N) Pierpont primes smaller than N, as opposed to the conjectured O(log log N) Mersenne primes in that range.
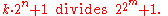
The left-hand side is a Pierpont prime when k is a power of 3; the right-hand side is a Fermat number.
, the largest known Pierpont prime is 3 × 27033641 + 1, whose primality was discovered by Michael Herder in 2011.
In the mathematics of paper folding
, the Huzita axioms define six of the seven types of fold possible. It has been shown that these folds are sufficient to allow any regular polygon
of N sides to be formed, as long as N > 3 and of the form 2m3nρ, where ρ is a product of distinct Pierpont primes. This is the same class of regular polygons as those that can be constructed with a compass, straightedge, and angle-trisector. Regular polygons which can be constructed with only compass and straightedge (constructible polygon
s) are the special case where n = 0 and ρ is a product of distinct Fermat primes, themselves a subset of Pierpont primes.
The smallest prime that is not a Pierpont (or Fermat) prime is 11, therefore the hendecagon
is the smallest regular polygon that cannot be constructed with compass, straightedge and angle trisector. All other regular n-gons with 3≤n≤21 can be constructed with compass, straightedge and trisector (if needed).
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
of the form
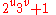
for some nonnegative integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s u and v. They are named after the mathematician James Pierpont
James Pierpont (mathematician)
James P. Pierpont was a Connecticut-born American mathematician. His father Cornelius Pierpont was a wealthy New Haven businessman. He did undergraduate studies at Worcester Polytechnic Institute, initially in mechanical engineering, but turned to mathematics. He went to Europe after graduating in...
.
It is possible to prove that if v = 0 and u > 0, then u must be a power of 2, making the prime a Fermat prime. If v is positive then u must also be positive, and the Pierpont prime is of the form 6k + 1 (because if u = 0 and v > 0 then 2u3v + 1 is an even number greater than 2 and therefore composite).
The first few Pierpont primes are:
- 2, 3, 5, 7, 1313 (number)13 is the natural number after 12 and before 14. It is the smallest number with eight letters in its name spelled out in English. It is also the first of the teens – the numbers 13 through 19 – the ages of teenagers....
, 1717 (number)17 is the natural number following 16 and preceding 18. It is prime.In spoken English, the numbers 17 and 70 are sometimes confused because they sound similar. When carefully enunciated, they differ in which syllable is stressed: 17 vs 70...
, 1919 (number)19 is the natural number following 18 and preceding 20. It is a prime number.In English speech, the numbers 19 and 90 are often confused. When carefully enunciated, they differ in which syllable is stressed: 19 vs 90...
, 3737 (number)37 is the natural number following 36 and preceding 38.-In mathematics:It is a prime number, the fifth lucky prime, the first irregular prime, the third unique prime and the third cuban prime of the form...
, 7373 (number)73 is the natural number following 72 and preceding 74. In English, it is the smallest integer with twelve letters in its spelled out name.- In mathematics :...
, 9797 (number)97 is the natural number following 96 and preceding 98.-In mathematics:97 is the 25th prime number , following 89 and preceding 101. 97 is a Proth prime as it is 3 × 25 + 1.The numbers 97, 907, 9007, 90007 and 900007 are happy primes...
, 109109 (number)109 is the natural number following 108 and preceding 110.-In mathematics:One hundred [and] nine is the 29th prime number, and also a Chen prime. The previous prime is 107, making them both twin primes...
, 163163 (number)163 is the natural number following 162 and preceding 164.-In mathematics:163 is a strong prime in the sense that it is greater than the arithmetic mean of its two neighboring primes...
, 193193 (number)193 is the natural number following 192 and preceding 194.-In mathematics:* 193 is an odd number* 193 is a centered 32-gonal number* 193 is a deficient number, as 1 is less than 193* 193 is a happy number* 193 is a lucky number...
, 257, 433, 487, 577, 769.
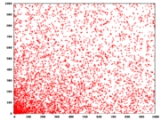
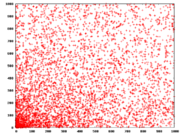
Distribution of Pierpont primes

Andrew Gleason
Andrew Mattei Gleason was an American mathematician and the eponym of Gleason's theorem and the Greenwood–Gleason graph. After briefly attending Berkeley High School he graduated from Roosevelt High School in Yonkers, then Yale University in 1942, where he became a Putnam Fellow...
conjectured there are infinitely many Pierpont primes. They are not particularly rare and there are few restrictions from algebraic factorisations, so there are no requirements like the Mersenne prime
Mersenne prime
In mathematics, a Mersenne number, named after Marin Mersenne , is a positive integer that is one less than a power of two: M_p=2^p-1.\,...
condition that the exponent must be prime. There are 36 Pierpont primes less than 106, 59 less than 109, 151 less than 1020, and 789 less than 10100; conjecturally there are O(log N) Pierpont primes smaller than N, as opposed to the conjectured O(log log N) Mersenne primes in that range.
Pierpont primes found as factors of Fermat numbers
As part of the ongoing worldwide search for factors of Fermat numbers, some Pierpont primes have been announced as factors. The following table gives values of m, k, and n such that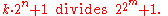
The left-hand side is a Pierpont prime when k is a power of 3; the right-hand side is a Fermat number.
| m | k | n | Year | Discoverer |
|---|---|---|---|---|
| 38 | 3 | 41 | 1903 | Cullen James Cullen (mathematician) Father James Cullen, S.J. was born at Drogheda, County Louth, Ireland.He studied mathematics at the Trinity College, Dublin for a while, but eventually turned to theology and was ordained as a Jesuit on 1 July 1901.... , Cunningham Allan Joseph Champneys Cunningham The British mathematician Allan Joseph Champneys Cunningham started a military career with the East India Company's Bengal Engineers. During 1871–1881, he was Instructor in Mathematics at the Thomason Civil Engineering College, Roorkee... & Western |
| 63 | 9 | 67 | 1956 | Robinson Raphael M. Robinson Raphael Mitchel Robinson was an American mathematician.Born in National City, California, Robinson was the youngest of four children of a lawyer and a teacher. He was awarded the BA , MA , and Ph.D. , all in mathematics, and all from the University of California, Berkeley. His Ph.D... |
| 207 | 3 | 209 | 1956 | Robinson |
| 452 | 27 | 455 | 1956 | Robinson |
| 9428 | 9 | 9431 | 1983 | Keller |
| 12185 | 81 | 12189 | 1993 | Dubner Harvey Dubner Harvey Dubner is a semi-retired engineer living in New Jersey, noted for his contributions to finding large prime numbers. In 1984, he and his son Robert collaborated in developing the 'Dubner cruncher', a board which used a commercial finite impulse response filter chip to speed up dramatically... |
| 28281 | 81 | 28285 | 1996 | Taura |
| 157167 | 3 | 157169 | 1995 | Young |
| 213319 | 3 | 213321 | 1996 | Young |
| 303088 | 3 | 303093 | 1998 | Young |
| 382447 | 3 | 382449 | 1999 | Cosgrave John B. Cosgrave Dr. John B. Cosgrave is an Irish mathematician specialising in number theory.-Other:In January 1999, while preparing some work for his students, he identified a highly structured prime number with exactly two thousand digits... & Gallot |
| 461076 | 9 | 461081 | 2003 | Nohara, Jobling, Woltman George Woltman George Woltman is the founder of the Great Internet Mersenne Prime Search , a distributed computing project researching Mersenne prime numbers using his software Prime95 and MPrime. He graduated from the Massachusetts Institute of Technology with degrees in computer science. He is presently... & Gallot |
| 672005 | 27 | 672007 | 2005 | Cooper Curtis Cooper (mathematician) Curtis Niles Cooper is an American mathematician. He currently is a professor at the University of Central Missouri, in the Department of Mathematics and Computer Science.... , Jobling, Woltman & Gallot |
| 2145351 | 3 | 2145353 | 2003 | Cosgrave, Jobling, Woltman & Gallot |
| 2478782 | 3 | 2478785 | 2003 | Cosgrave, Jobling, Woltman & Gallot |
, the largest known Pierpont prime is 3 × 27033641 + 1, whose primality was discovered by Michael Herder in 2011.
In the mathematics of paper folding
Mathematics of paper folding
The art of origami or paper folding has received a considerable amount of mathematical study. Fields of interest include a given paper model's flat-foldability and the use of paper folds to solve mathematical equations.-Flat folding:The construction of origami models is sometimes shown as crease...
, the Huzita axioms define six of the seven types of fold possible. It has been shown that these folds are sufficient to allow any regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
of N sides to be formed, as long as N > 3 and of the form 2m3nρ, where ρ is a product of distinct Pierpont primes. This is the same class of regular polygons as those that can be constructed with a compass, straightedge, and angle-trisector. Regular polygons which can be constructed with only compass and straightedge (constructible polygon
Constructible polygon
In mathematics, a constructible polygon is a regular polygon that can be constructed with compass and straightedge. For example, a regular pentagon is constructible with compass and straightedge while a regular heptagon is not....
s) are the special case where n = 0 and ρ is a product of distinct Fermat primes, themselves a subset of Pierpont primes.
The smallest prime that is not a Pierpont (or Fermat) prime is 11, therefore the hendecagon
Hendecagon
In geometry, a hendecagon is an 11-sided polygon....
is the smallest regular polygon that cannot be constructed with compass, straightedge and angle trisector. All other regular n-gons with 3≤n≤21 can be constructed with compass, straightedge and trisector (if needed).

