Mathematics of paper folding
Encyclopedia
The art
of origami
or paper folding has received a considerable amount of mathematical
study. Fields of interest include a given paper model's flat-foldability (whether the model can be flattened without damaging it) and the use of paper folds to solve mathematical equations
.
problems. There are four mathematical rules for producing flat-foldable origami crease pattern
s:
Paper exhibits zero Gaussian curvature
at all points on its surface, and only folds naturally along lines of zero curvature. Curved surfaces which can't be flattened can be produced using a non-folded crease in the paper, as is easily done with wet paper or a fingernail.
Assigning a crease pattern mountain and valley folds in order to produce a flat model has been proven by Marshall Bern and Barry Hayes to be NP complete. Further references and technical results are discussed in Part II of Geometric Folding Algorithms.
— are proven to be unsolvable using compass and straightedge
, but can be solved using only a few paper folds. Paper fold strips can be constructed to solve equations up to degree 4. The Huzita–Hatori axioms are an important contribution to this field of study. These describe what can be constructed using a sequence of creases with at most two point or line alignments at once. Complete methods for solving all equations up to degree 4 by applying methods satisfying these axioms are discussed in detail in Geometric Origami.
The accompanying diagram shows Haga's first theorem:
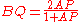
Interestingly the function changing the length AP to QC is self inverse. Let x be AP then a number of other lengths are also rational functions of x. For example:
can be solved by first creasing a square of paper into three equal strips as shown in the diagram. Then the bottom edge is positioned so the corner point P is on the top edge and the crease mark on the edge meets the other crease mark Q. The length PB will then be the cube root of 2 times the length of AP.
The edge with the crease mark is considered a marked straightedge, something which is not allowed in compass and straightedge constructions. Using a marked straightedge in this way is called a neusis construction
in geometry.
is another of the classical problems that cannot be solved using a compass and unmarked ruler but can be solved using origami. The angle CAB is trisected by making folds PP' and QQ' parallel to the base with QQ' halfway in between. Then point P is folded over to lie on line AC and at the same time point A is made to lie on line QQ' at A'. The angle A'AB is one third of the original angle CAB. This is because PAQ, QAA' and A'AB are three identical triangles. Aligning the two points on the two lines is another neusis construction as in the solution to doubling the cube.
, treating the folds as hinges joining two flat, rigid surfaces, such as sheet metal
, has great practical importance. For example, the Miura map fold
is a rigid fold that has been used to deploy large solar panel arrays for space satellites.
The napkin folding problem
is the problem of whether a square or rectangle of paper can be folded so the perimeter of the flat figure is greater than that of the original square.
Curved origami also poses a (very different) set of mathematical challenges.
Curved origami allows the paper to form developable surface
s that are not flat.
Wet-folding
origami allows an even greater range of shapes.
The maximum number of times an incompressible material can be folded has been derived. With each fold a certain amount of paper is lost to potential folding. The loss function
for folding paper in half in a single direction was given to be
, where L is the minimum length of the paper (or other material), t is the material's thickness, and n is the number of folds possible. The distances L and t must be expressed in the same units, such as inches. This function was derived by Britney Gallivan
in 2001 (then only a high school
student) who then folded a sheet of paper in half 12 times, contrary to the popular belief that paper of any size could be folded at most eight times. She also derived the equation for folding in alternate directions.
The fold-and-cut problem asks what shapes can be obtained by folding a piece of paper flat, and making a single straight complete cut. The solution, known as the Fold and Cut Theorem, states that any shape with straight sides can be obtained.
Art
Art is the product or process of deliberately arranging items in a way that influences and affects one or more of the senses, emotions, and intellect....
of origami
Origami
is the traditional Japanese art of paper folding, which started in the 17th century AD at the latest and was popularized outside Japan in the mid-1900s. It has since then evolved into a modern art form...
or paper folding has received a considerable amount of mathematical
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
study. Fields of interest include a given paper model's flat-foldability (whether the model can be flattened without damaging it) and the use of paper folds to solve mathematical equations
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
.
Flat folding
The construction of origami models is sometimes shown as crease patterns. The major question about such crease patterns is whether a given crease pattern can be folded to a flat model, and if so, how to fold them; this is an NP-complete problem. Related problems when the creases are orthogonal are called map foldingMap folding
In combinatorial mathematics the map folding problem is the question of how many ways there are to fold a rectangular map along its creases. A related problem called the stamp folding problem is how many ways there are to fold a strip of stamps....
problems. There are four mathematical rules for producing flat-foldable origami crease pattern
Crease pattern
A Crease Pattern is an origami diagram type that consists of all or most of the creases in the final model, rendered into one image. This comes in handy for diagramming complex and super-complex models, where the model is often not simple enough to diagram efficiently.The use of crease patterns...
s:
- crease patterns are two colorable
- Maekawa's theorem: at any vertex the number of valley and mountain folds always differ by two in either direction
- Kawasaki's theoremKawasaki's theoremKawasaki's theorem is a theorem in the mathematics of paper folding, named after Toshikazu Kawasaki, that gives a criterion for determining whether a crease pattern with a single vertex may be folded to form a flat figure.- Statement of the theorem :...
: at any vertex, the sum of all the odd angles adds up to 180 degrees, as do the even. - a sheet can never penetrate a fold.
Paper exhibits zero Gaussian curvature
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
at all points on its surface, and only folds naturally along lines of zero curvature. Curved surfaces which can't be flattened can be produced using a non-folded crease in the paper, as is easily done with wet paper or a fingernail.
Assigning a crease pattern mountain and valley folds in order to produce a flat model has been proven by Marshall Bern and Barry Hayes to be NP complete. Further references and technical results are discussed in Part II of Geometric Folding Algorithms.
Huzita–Hatori axioms
Some classical construction problems of geometry — namely trisecting an arbitrary angle, or doubling the cubeDoubling the cube
Doubling the cube is one of the three most famous geometric problems unsolvable by compass and straightedge construction...
— are proven to be unsolvable using compass and straightedge
Compass and straightedge
Compass-and-straightedge or ruler-and-compass construction is the construction of lengths, angles, and other geometric figures using only an idealized ruler and compass....
, but can be solved using only a few paper folds. Paper fold strips can be constructed to solve equations up to degree 4. The Huzita–Hatori axioms are an important contribution to this field of study. These describe what can be constructed using a sequence of creases with at most two point or line alignments at once. Complete methods for solving all equations up to degree 4 by applying methods satisfying these axioms are discussed in detail in Geometric Origami.
Constructions
As a result of origami study through the application of geometric principles, methods such as Haga's theorem have allowed paperfolders to accurately fold the side of a square into thirds, fifths, sevenths, and ninths. Other theorems and methods have allowed paperfolders to get other shapes from a square, such as equilateral triangles, pentagons, hexagons, and special rectangles such as the golden rectangle and the silver rectangle. Methods for folding most regular polygons up to and including the regular 19-gon have been developed.Haga's theorems
The side of a square can be divided at an arbitrary rational fraction in a variety of ways. Haga's theorems say that a particular set of constructions can be used for such divisions. Surprisingly few folds are necessary to generate large odd fractions. For instance can be generated with three folds; first halve a side, then use Haga's theorem twice to produce first and then .The accompanying diagram shows Haga's first theorem:
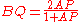
Interestingly the function changing the length AP to QC is self inverse. Let x be AP then a number of other lengths are also rational functions of x. For example:
| AP | BQ | QC | AR | PQ |
|---|---|---|---|---|
 |
 |
 |
 |
 |
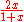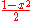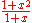Doubling the cube
The classical problem of doubling the cubeDoubling the cube
Doubling the cube is one of the three most famous geometric problems unsolvable by compass and straightedge construction...
can be solved by first creasing a square of paper into three equal strips as shown in the diagram. Then the bottom edge is positioned so the corner point P is on the top edge and the crease mark on the edge meets the other crease mark Q. The length PB will then be the cube root of 2 times the length of AP.
The edge with the crease mark is considered a marked straightedge, something which is not allowed in compass and straightedge constructions. Using a marked straightedge in this way is called a neusis construction
Neusis construction
The neusis is a geometric construction method that was used in antiquity by Greek mathematicians.- Geometric construction :The neusis construction consists of fitting a line element of given length in between two given lines , in such a way that the line element, or its...
in geometry.
Trisecting an angle
Angle trisectionAngle trisection
Angle trisection is a classic problem of compass and straightedge constructions of ancient Greek mathematics. It concerns construction of an angle equal to one-third of a given arbitrary angle, using only two tools: an un-marked straightedge, and a compass....
is another of the classical problems that cannot be solved using a compass and unmarked ruler but can be solved using origami. The angle CAB is trisected by making folds PP' and QQ' parallel to the base with QQ' halfway in between. Then point P is folded over to lie on line AC and at the same time point A is made to lie on line QQ' at A'. The angle A'AB is one third of the original angle CAB. This is because PAQ, QAA' and A'AB are three identical triangles. Aligning the two points on the two lines is another neusis construction as in the solution to doubling the cube.
Related problems
The problem of rigid origamiRigid origami
Rigid origami is a branch of origami which is concerned with folding structures using flat rigid sheets joined by hinges. It is a part of the study of the mathematics of paper folding, it can be considered as a type of mechanical linkage, and has great practical utility. For instance it was used in...
, treating the folds as hinges joining two flat, rigid surfaces, such as sheet metal
Sheet metal
Sheet metal is simply metal formed into thin and flat pieces. It is one of the fundamental forms used in metalworking, and can be cut and bent into a variety of different shapes. Countless everyday objects are constructed of the material...
, has great practical importance. For example, the Miura map fold
Miura map fold
The is a rigid fold that has been used to simulate large solar panel arrays for space satellites in the Japanese 1995 Space Flight Unit. It was invented by Japanese astrophysicist Koryo Miura...
is a rigid fold that has been used to deploy large solar panel arrays for space satellites.
The napkin folding problem
Napkin folding problem
The napkin folding problem in geometry explores whether folding a square or a rectangular napkin can increase its perimeter. The problem is known under several names, including the Margulis napkin problem, suggesting it is due to Grigory Margulis, and the Arnold's rouble problem referring to...
is the problem of whether a square or rectangle of paper can be folded so the perimeter of the flat figure is greater than that of the original square.
Curved origami also poses a (very different) set of mathematical challenges.
Curved origami allows the paper to form developable surface
Developable surface
In mathematics, a developable surface is a surface with zero Gaussian curvature. That is, it is a "surface" that can be flattened onto a plane without distortion . Conversely, it is a surface which can be made by transforming a plane...
s that are not flat.
Wet-folding
Wet-folding
Wet-folding is an origami technique developed by Akira Yoshizawa that employs water to dampen the paper so that it can be manipulated more easily. This process adds an element of sculpture to origami, which is otherwise purely geometric. Wet-folding is used very often by professional folders for...
origami allows an even greater range of shapes.
The maximum number of times an incompressible material can be folded has been derived. With each fold a certain amount of paper is lost to potential folding. The loss function
Loss function
In statistics and decision theory a loss function is a function that maps an event onto a real number intuitively representing some "cost" associated with the event. Typically it is used for parameter estimation, and the event in question is some function of the difference between estimated and...
for folding paper in half in a single direction was given to be
, where L is the minimum length of the paper (or other material), t is the material's thickness, and n is the number of folds possible. The distances L and t must be expressed in the same units, such as inches. This function was derived by Britney GallivanBritney Gallivan
Britney Crystal Gallivan of Pomona, California, is best known for determining the maximum number of times which paper or other materials can be folded.-Biography:...
in 2001 (then only a high school
High school
High school is a term used in parts of the English speaking world to describe institutions which provide all or part of secondary education. The term is often incorporated into the name of such institutions....
student) who then folded a sheet of paper in half 12 times, contrary to the popular belief that paper of any size could be folded at most eight times. She also derived the equation for folding in alternate directions.
The fold-and-cut problem asks what shapes can be obtained by folding a piece of paper flat, and making a single straight complete cut. The solution, known as the Fold and Cut Theorem, states that any shape with straight sides can be obtained.
See also
- Napkin folding problemNapkin folding problemThe napkin folding problem in geometry explores whether folding a square or a rectangular napkin can increase its perimeter. The problem is known under several names, including the Margulis napkin problem, suggesting it is due to Grigory Margulis, and the Arnold's rouble problem referring to...
- Map foldingMap foldingIn combinatorial mathematics the map folding problem is the question of how many ways there are to fold a rectangular map along its creases. A related problem called the stamp folding problem is how many ways there are to fold a strip of stamps....
- Regular paperfolding sequenceRegular paperfolding sequenceIn mathematics the regular paperfolding sequence, also known as the dragon curve sequence, is an infinite automatic sequence of 0s and 1s defined as the limit of the following process:...
(for example, the Dragon curveDragon curveA dragon curve is any member of a family of self-similar fractal curves, which can be approximated by recursive methods such as Lindenmayer systems.-Heighway dragon:...
)
External links
- Paper Folding Geometry at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Dividing a Segment into Equal Parts by Paper Folding at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Britney Gallivan has solved the Paper Folding Problem