Pisano period
Encyclopedia
In number theory
, the nth Pisano period, written π(n), is the period
with which the sequence
of Fibonacci number
s, modulo
n repeats. For example, the Fibonacci numbers modulo 3 are , 1, 1, 2, 0, 2, 2, 1, 0, 1, 1, etc., with the first eight numbers repeating, so π(3) = 8.
Pisano periods are named after Leonardo Pisano, better known as Fibonacci
. The existence of periodic functions in Fibonacci numbers was noted by Joseph Louis Lagrange
in 1774.
Onward the Pisano periods are 10
, 24, 28
, 48
, 40
, 24, 36
, 24, 18
, 60, 16, 30
, 48, 24, 100
...
For n > 2 the period is even, because alternatingly F(n)2 is one more and one less than F(n − 1)F(n + 1) (Cassini's identity).
The period is relatively small, 4k + 2, for n = F (2k) + F (2k + 2), i.e. Lucas number
L (2k + 1), with k a positive integer. This is because F(−2k − 1) = F (2k + 1) and F(−2k) = −F (2k), and the latter is congruent to F(2k + 2) modulo n, showing that the period is a divisor of 4k + 2; the period cannot be 2k + 1 or less because the first 2k + 1 Fibonacci numbers from 0 are less than n.
The second half of the cycle, which is of course equal to the part on the left of 0, consists of alternatingly numbers F(2m + 1) and n − F(2m), with m decreasing.
Furthermore, the period is 4k for n = F(2k), and 8k + 4 for n = F(2k + 1).
The number of occurrences of 0 per cycle is 1, 2, or 4. Let p be the number after the first 0 after the combination 0, 1. Let the distance between the 0s be q.
For generalized Fibonacci sequences (satisfying the same recurrence relation, but with other initial values, e.g. the Lucas numbers) the number of occurrences of 0 per cycle is 0, 1, 2, or 4. Also, it can be proven that
with equality if and only if n = 2 · 5k, for k ≥ 1, the first examples being π(10) = 60 and π(50) = 300.
.
If m and n are coprime
, then
by the Chinese remainder theorem
: two numbers are congruent modulo mn if and only if they are congruent modulo m and modulo n, assuming these latter are coprime. For example,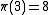
and 
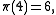so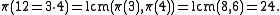 
Thus it suffices to compute Pisano periods for prime power
s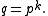
For prime numbers p, these can be analyzed by using Binet's formula: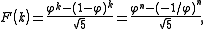
where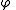 
is the golden ratio
If 5 is a quadratic residue modulo p (and
), then 
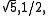and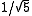 
can be expressed as integers modulo p, and thus Binet's formula can be expressed over integers modulo p, and thus the Pisano period divides the totient 
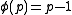, since any power (such as 
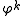) has period dividing 
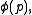as this is the order of the group of units modulo p.
This first occurs for n = 11, where 42 = 16 ≡ 5 (mod 11) and 2 · 6 = 12 ≡ 1 (mod 11) and 4 · 3 = 12 ≡ 1 (mod 11) so 4 = √5, 6 = 1/2 and 1/√5 = 3, yielding φ = (1 + 4) · 6 = 30 ≡ 8 (mod 11) and the formula
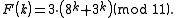
Another example, which shows that the period can properly divide p − 1, is π(29) = 14.
If 5 is not a quadratic residue (and p ≠ 2, 5), then Binet's formula is instead defined over the quadratic extension field (Z/p)[√5], which has p2 elements and whose group of units thus has order p2 − 1, and thus the Pisano period divides p2 − 1. For example, for p = 3 one has π(3) = 8 which equals 32 − 1 = 8; for p = 7, one has π(7) = 16, which properly divides 72 − 1 = 48.
This analysis fails for p = 2 and p = 5 since in these cases 2 and 5 are zero divisor
s, so one must be careful in interpreting 1/2 or √5. For p = 2, 5 is congruent to 1 mod 2, but the Pisano period is not p − 1 = 1, but rather 3. For p = 5, the Pisano period is π(5) = 20 = 5(5 − 1), which does not divide p − 1 = 4 or p2 − 1 = 24.
it follows that the sum of π(n) consecutive Fibonacci numbers is a multiple of n.
Moreover, for the values in the table the sum of π(n) consecutive Fibonacci numbers is n times the (π(n)/2 + 1)th element:
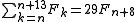
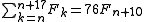
, where the sequence is depicted as tiles on a wall.
. The period is a divisor
of π(n). The number of occurrences of 0 per cycle is 0, 1, 2, or 4. If n is not a prime the cycles include those that are multiples of the cycles for the divisors. For example, for n = 10 the extra cycles include those for n = 2 multiplied by 5, and for n = 5 multiplied by 2.
Table of the extra cycles:
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the nth Pisano period, written π(n), is the period
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
with which the sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s, modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
n repeats. For example, the Fibonacci numbers modulo 3 are , 1, 1, 2, 0, 2, 2, 1, 0, 1, 1, etc., with the first eight numbers repeating, so π(3) = 8.
Pisano periods are named after Leonardo Pisano, better known as Fibonacci
Fibonacci
Leonardo Pisano Bigollo also known as Leonardo of Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, or, most commonly, simply Fibonacci, was an Italian mathematician, considered by some "the most talented western mathematician of the Middle Ages."Fibonacci is best known to the modern...
. The existence of periodic functions in Fibonacci numbers was noted by Joseph Louis Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
in 1774.
Tables
The first Pisano periods and their cycles (with spaces before the zeros for readability) are:| n | π(n) | nr. of 0s | cycle |
|---|---|---|---|
| 1 | 1 | 1 | 0 |
| 2 | 3 | 1 | 011 |
| 3 | 8 | 2 | 0112 0221 |
| 4 | 6 | 1 | 011231 |
| 5 | 20 20 (number) 20 is the natural number following 19 and preceding 21. A group of twenty units may also be referred to as a score.-In mathematics:*20 is the basis for vigesimal number systems.... |
4 | 01123 03314 04432 02241 |
| 6 | 24 24 (number) 24 is the natural number following 23 and preceding 25.The SI prefix for 1024 is yotta , and for 10−24 yocto... |
2 | 011235213415 055431453251 |
| 7 | 16 16 (number) 16 is the natural number following 15 and preceding 17. 16 is a composite number, and a square number, being 42 = 4 × 4. It is the smallest number with exactly five divisors, its proper divisors being , , and .... |
2 | 01123516 06654261 |
| 8 | 12 12 (number) 12 is the natural number following 11 and preceding 13.The word "twelve" is the largest number with a single-morpheme name in English. Etymology suggests that "twelve" arises from the Germanic compound twalif "two-leftover", so a literal translation would yield "two remaining [after having ten... |
2 | 011235 055271 |
| 9 | 24 | 2 | 011235843718 088764156281 |
| 10 | 60 60 (number) 60 is the natural number following 59 and preceding 61. Being three times twenty, 60 is called "three score" in some older literature.-In mathematics:... |
4 | 011235831459437 077415617853819 099875279651673 033695493257291 |
Onward the Pisano periods are 10
10 (number)
10 is an even natural number following 9 and preceding 11.-In mathematics:Ten is a composite number, its proper divisors being , and...
, 24, 28
28 (number)
28 is the natural number following 27 and preceding 29.-In mathematics:It is a composite number, its proper divisors being 1, 2, 4, 7, and 14....
, 48
48 (number)
48 is the natural number following 47 and preceding 49. It is one third of a gross or four dozens.- In mathematics :Forty-eight is a double factorial of 6, a highly composite number. Like all other multiples of 6, it is a semiperfect number. 48 is the second 17-gonal number.48 is in abundance...
, 40
40 (number)
40 is the natural number following 39 and preceding 41.Despite being related to the word "four" , 40 is spelled "forty", and not "fourty"...
, 24, 36
36 (number)
36 is the natural number following 35 and preceding 37.- In mathematics :36 is both the square of 6 and a triangular number, making it a square triangular number...
, 24, 18
18 (number)
18 is the natural number following 17 and preceding 19.In speech, the numbers 18 and 80 are sometimes confused. When carefully enunciated, they differ in which syllable is stressed: 18 vs 80 . However, in dates such as 1864, or when contrasting numbers in the teens, such as 17, 18, 19, the stress...
, 60, 16, 30
30 (number)
30 is the natural number following 29 and preceding 31.-In mathematics:30 is the sum of the first four squares, which makes it a square pyramidal number.It is a primorial and is the smallest Giuga number....
, 48, 24, 100
100 (number)
100 is the natural number following 99 and preceding 101.-In mathematics:One hundred is the square of 10...
...
For n > 2 the period is even, because alternatingly F(n)2 is one more and one less than F(n − 1)F(n + 1) (Cassini's identity).
The period is relatively small, 4k + 2, for n = F (2k) + F (2k + 2), i.e. Lucas number
Lucas number
The Lucas numbers are an integer sequence named after the mathematician François Édouard Anatole Lucas , who studied both that sequence and the closely related Fibonacci numbers...
L (2k + 1), with k a positive integer. This is because F(−2k − 1) = F (2k + 1) and F(−2k) = −F (2k), and the latter is congruent to F(2k + 2) modulo n, showing that the period is a divisor of 4k + 2; the period cannot be 2k + 1 or less because the first 2k + 1 Fibonacci numbers from 0 are less than n.
| k | n | π(n) | first half of cycle (with selected second halfs) |
|---|---|---|---|
| 1 | 4 | 6 | 0, 1, 1, 2 |
| 2 | 11 | 10 | 0, 1, 1, 2, 3, 5 |
| 3 | 29 | 14 | 0, 1, 1, 2, 3, 5, 8, 13 |
| 4 | 76 | 18 | 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 |
| 5 | 199 | 22 | 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 |
| 6 | 521 | 26 | 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 |
| 7 | 1364 | 30 | 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610 |
| 8 | 3571 | 34 | 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597 |
| 9 | 9349 | 38 | 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181 |
The second half of the cycle, which is of course equal to the part on the left of 0, consists of alternatingly numbers F(2m + 1) and n − F(2m), with m decreasing.
Furthermore, the period is 4k for n = F(2k), and 8k + 4 for n = F(2k + 1).
The number of occurrences of 0 per cycle is 1, 2, or 4. Let p be the number after the first 0 after the combination 0, 1. Let the distance between the 0s be q.
- There is one 0 in a cycle, obviously, if p = 1. This is only possible if q is even or n is 1 or 2.
- Otherwise there are two 0s in a cycle if p2 ≡ 1. This is only possible if q is even.
- Otherwise there are four 0s in a cycle. This is the case if q is odd and n is not 1 or 2.
For generalized Fibonacci sequences (satisfying the same recurrence relation, but with other initial values, e.g. the Lucas numbers) the number of occurrences of 0 per cycle is 0, 1, 2, or 4. Also, it can be proven that
- π(n) ≤ 6n,
with equality if and only if n = 2 · 5k, for k ≥ 1, the first examples being π(10) = 60 and π(50) = 300.
Number theory
Pisano periods can be analyzed using algebraic number theoryAlgebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
.
If m and n are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
, then
by the Chinese remainder theoremChinese remainder theorem
The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
: two numbers are congruent modulo mn if and only if they are congruent modulo m and modulo n, assuming these latter are coprime. For example,
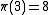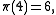and so 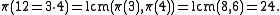Thus it suffices to compute Pisano periods for prime powerPrime power
In mathematics, a prime power is a positive integer power of a prime number.For example: 5=51, 9=32 and 16=24 are prime powers, while6=2×3, 15=3×5 and 36=62=22×32 are not...
s
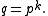
For prime numbers p, these can be analyzed by using Binet's formula:
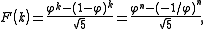where 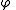is the golden ratioGolden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
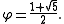
If 5 is a quadratic residue modulo p (and
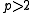), then 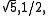and 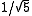can be expressed as integers modulo p, and thus Binet's formula can be expressed over integers modulo p, and thus the Pisano period divides the totient 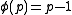, since any power (such as 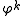) has period dividing 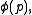as this is the order of the group of units modulo p.This first occurs for n = 11, where 42 = 16 ≡ 5 (mod 11) and 2 · 6 = 12 ≡ 1 (mod 11) and 4 · 3 = 12 ≡ 1 (mod 11) so 4 = √5, 6 = 1/2 and 1/√5 = 3, yielding φ = (1 + 4) · 6 = 30 ≡ 8 (mod 11) and the formula
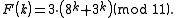
Another example, which shows that the period can properly divide p − 1, is π(29) = 14.
If 5 is not a quadratic residue (and p ≠ 2, 5), then Binet's formula is instead defined over the quadratic extension field (Z/p)[√5], which has p2 elements and whose group of units thus has order p2 − 1, and thus the Pisano period divides p2 − 1. For example, for p = 3 one has π(3) = 8 which equals 32 − 1 = 8; for p = 7, one has π(7) = 16, which properly divides 72 − 1 = 48.
This analysis fails for p = 2 and p = 5 since in these cases 2 and 5 are zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s, so one must be careful in interpreting 1/2 or √5. For p = 2, 5 is congruent to 1 mod 2, but the Pisano period is not p − 1 = 1, but rather 3. For p = 5, the Pisano period is π(5) = 20 = 5(5 − 1), which does not divide p − 1 = 4 or p2 − 1 = 24.
Sums
Using- F(0) + F(1) + F(2) + … + F(k) = F(k + 2) − 1,
it follows that the sum of π(n) consecutive Fibonacci numbers is a multiple of n.
Moreover, for the values in the table the sum of π(n) consecutive Fibonacci numbers is n times the (π(n)/2 + 1)th element:
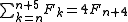
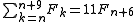
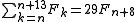
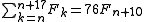
Powers of 10
The Pisano periods when n is a power of 10 are 60, 300, 1500, 15000, 150000, ... . Dov Jarden proved that for n greater than 2 the periodicity mod 10n is 15·10n−1.Cultural references
The Fibonacci sequence modulo 5 (Pisano period 20, with 4 zeros) is featured in the episode "The Case of the Willing Parrot" of the TV MathnetMathnet
Mathnet is a segment on the children's television show Square One, of which five seasons were produced . This parody of Dragnet featured detectives at the Los Angeles Police Department who solved mysteries using their mathematical skills. There were two main characters: detectives Kate Monday and...
, where the sequence is depicted as tiles on a wall.
Fibonacci integer sequences modulo n
One can consider Fibonacci integer sequences and take them modulo n, or put differently, consider Fibonacci sequences in the ring Z/nCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
. The period is a divisor
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
of π(n). The number of occurrences of 0 per cycle is 0, 1, 2, or 4. If n is not a prime the cycles include those that are multiples of the cycles for the divisors. For example, for n = 10 the extra cycles include those for n = 2 multiplied by 5, and for n = 5 multiplied by 2.
Table of the extra cycles:
| n | multiples | other cycles |
|---|---|---|
| 1 | ||
| 2 | 0 | |
| 3 | 0 | |
| 4 | 0, 022 | 033213 |
| 5 | 0 | 1342 |
| 6 | 0, 0224 0442, 033 | |
| 7 | 0 | 02246325 05531452, 03362134 04415643 |
| 8 | 0, 022462, 044, 066426 | 033617 077653, 134732574372, 145167541563 |
| 9 | 0, 0336 0663 | 022461786527 077538213472, 044832573145 055167426854 |
| 10 | 0, 02246 06628 08864 04482, 055, 2684 | 134718976392 |