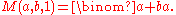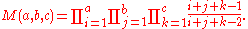Plane partition
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a plane partition (see also solid partition for three-dimensional array) is a two-dimensional array of nonnegative integers
 which are nonincreasing from left to right and top to bottom:
which are nonincreasing from left to right and top to bottom: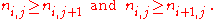
Thinking of the stack of
 unit cubes placed on (i,j)-square, we obtain a solid (or 3-dimensional) partition.
unit cubes placed on (i,j)-square, we obtain a solid (or 3-dimensional) partition.Define the sum of the plane partition by
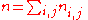
and let PL(n) denote the number of plane partitions with sum n.
For example, there are six plane partitions with sum 3:
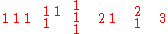
so PL(3) = 6.
Generating function
By a result of Percy MacMahonPercy Alexander MacMahon
Percy Alexander MacMahon was a mathematician, especially noted in connection with the partitions of numbers and enumerative combinatorics.-Early life:...
, the generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
for PL(n) can be calculated by
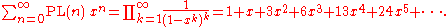
This is usually referred to as the MacMahon function.
This formula is the 2-dimensional analogue of Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
's product formula for the number of integer partitions
Partition (number theory)
In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
of n. There is no analogous formula for partitions in higher dimensions.
MacMahon formula
Denote by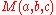 the number of solid partitions which fit into
the number of solid partitions which fit into 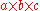 box. In the planar case, we obtain the binomial coefficient
box. In the planar case, we obtain the binomial coefficientBinomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s:
MacMahon formula is the multiplicative formula for general values of
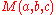 :
:
This formula was obtained by Percy MacMahon
Percy Alexander MacMahon
Percy Alexander MacMahon was a mathematician, especially noted in connection with the partitions of numbers and enumerative combinatorics.-Early life:...
and was later rewritten in this form by Ian Macdonald
Ian G. Macdonald
Ian Grant Macdonald is a British mathematician known for his contributions to symmetric functions, special functions, Lie algebra theory and other aspects of algebraic combinatorics ....
.