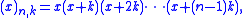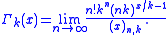Pochhammer k-symbol
Encyclopedia
In the mathematical theory of special functions
, the Pochhammer k-symbol and the k-gamma function, introduced by Rafael Díaz and Eddy Pariguan, are generalizations of the Pochhammer symbol
and gamma function
. They differ from the Pochhammer symbol and gamma function in that they can be related to a general arithmetic progression
in the same manner as those are related to the sequence of consecutive integer
s.
The Pochhammer k-symbol (x)n,k is defined as
and the k-gamma function Γk, with k > 0, is defined as
When k = 1 the standard Pochhammer symbol and gamma function are obtained.
Díaz and Pariguan use these definitions to demonstrate a number of properties of the hypergeometric function. Although Díaz and Pariguan restrict these symbols to k > 0, the Pochhammer k-symbol as they define it is well-defined for all real k, and for negative k gives the falling factorial, while for k = 0 it reduces to the power
xn.
The Díaz and Pariguan paper does not address the many analogies between the Pochhammer k-symbol and the power function, such as the fact that the binomial theorem
can be extended to Pochhammer k-symbols. It is true, however, that many equations involving the power function xn continue to hold when xn is replaced by (x)n,k.
Special functions
Special functions are particular mathematical functions which have more or less established names and notations due to their importance in mathematical analysis, functional analysis, physics, or other applications....
, the Pochhammer k-symbol and the k-gamma function, introduced by Rafael Díaz and Eddy Pariguan, are generalizations of the Pochhammer symbol
Pochhammer symbol
In mathematics, the Pochhammer symbol introduced by Leo August Pochhammer is the notation ', where is a non-negative integer. Depending on the context the Pochhammer symbol may represent either the rising factorial or the falling factorial as defined below. Care needs to be taken to check which...
and gamma function
Gamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
. They differ from the Pochhammer symbol and gamma function in that they can be related to a general arithmetic progression
Arithmetic progression
In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
in the same manner as those are related to the sequence of consecutive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s.
The Pochhammer k-symbol (x)n,k is defined as
and the k-gamma function Γk, with k > 0, is defined as
When k = 1 the standard Pochhammer symbol and gamma function are obtained.
Díaz and Pariguan use these definitions to demonstrate a number of properties of the hypergeometric function. Although Díaz and Pariguan restrict these symbols to k > 0, the Pochhammer k-symbol as they define it is well-defined for all real k, and for negative k gives the falling factorial, while for k = 0 it reduces to the power
Exponentiation
Exponentiation is a mathematical operation, written as an, involving two numbers, the base a and the exponent n...
xn.
The Díaz and Pariguan paper does not address the many analogies between the Pochhammer k-symbol and the power function, such as the fact that the binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
can be extended to Pochhammer k-symbols. It is true, however, that many equations involving the power function xn continue to hold when xn is replaced by (x)n,k.