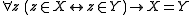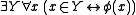Pocket set theory
Encyclopedia
Pocket set theory is an alternative set theory
in which there are only two infinite cardinals. The theory is authored by American mathematician Randall M. Holmes, although the basic idea was suggested by Rudy Rucker
in his Infinity and the Mind.
Thus, there are reasons to think that Cantor's infinite hierarchy of the infinites is superfluous. Pocket set theory is a “minimalistic” set theory that allows for only two infinites: the cardinality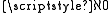
of the (standard) natural numbers and the cardinality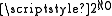 
of the (standard) reals.
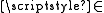. Ordinary variables are upper case X, Y, etc. In the intended interpretation, the variables these stand for classes
, and the atomic formula
means "class X is an element of class Y". A set is a class that is an element of a class. Small case variables x, y, etc. stand for sets. A proper class is a class that is not a set. Two classes are equinumerous
iff a bijection
exists between them. A class is infinite iff it is equinumerous with one of its proper subclasses. The axioms of PST are
)
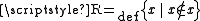2. The empty class is a set. (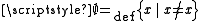
)
3. The singleton class of the empty set is a set.
4. The Russell class is infinite.
5. Every finite class is a set.
Once the above facts are settled, the following results can be proved:
5. The class V of sets (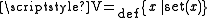
) consists of all hereditarily countable sets.
6. Every proper class has the cardinality
.
7. The union class of a set is a set.
PST also verifies
The theory neither approves nor rejects well-foundedness.
Alternative set theory
Generically, an alternative set theory is an alternative mathematical approach to the concept of set. It is a proposed alternative to the standard set theory.Some of the alternative set theories are:*the theory of semisets...
in which there are only two infinite cardinals. The theory is authored by American mathematician Randall M. Holmes, although the basic idea was suggested by Rudy Rucker
Rudy Rucker
Rudolf von Bitter Rucker is an American mathematician, computer scientist, science fiction author, and philosopher, and is one of the founders of the cyberpunk literary movement. The author of both fiction and non-fiction, he is best known for the novels in the Ware Tetralogy, the first two of...
in his Infinity and the Mind.
Arguments supporting PST
There are at least two independent arguments in favor of a small set theory like PST.- One can get the impression from mathematical practice outside set theory that there are “only two infinite cardinals which demonstrably ‘occur in nature’ (the cardinality of the natural numbers and the cardinality of the continuum),” therefore “set theory produces far more superstructure than is needed to support classical mathematics.” Although it may be an exaggeration (one can get into a situation in which one has to talk about arbitrary sets of real numbers or real functions), with some technical tricks a considerable portion of mathematics can be reconstructed within PST; certainly enough for most of its practical applications.
- A second argument arises from foundationalFoundations of mathematicsFoundations of mathematics is a term sometimes used for certain fields of mathematics, such as mathematical logic, axiomatic set theory, proof theory, model theory, type theory and recursion theory...
considerations. Most of mathematics can be implementedImplementation of mathematics in set theoryThis article examines the implementation of mathematical concepts in set theory. The implementation of a number of basic mathematical concepts is carried out in parallel in ZFC and in NFU, the version of Quine's New Foundations shown to be consistent by R. B...
in standard set theory or one of its large alternatives. Set theories, on the other hand, are introduced in terms of a logical system; in most cases it is first-order logicFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
. The syntax and semantics of first-order logic, on the other hand, is built on set-theoretical grounds. Thus, there is a foundational circularity, which forces us to choose as weak a theory as possible for bootstrappingBootstrappingBootstrapping or booting refers to a group of metaphors that share a common meaning: a self-sustaining process that proceeds without external help....
. This line of thought, again, leads to small set theories.
Thus, there are reasons to think that Cantor's infinite hierarchy of the infinites is superfluous. Pocket set theory is a “minimalistic” set theory that allows for only two infinites: the cardinality
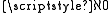of the (standard) natural numbers and the cardinality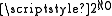 Cardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
of the (standard) reals.
The theory
PST uses standard first-order language with identity and the binary relation symbol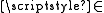. Ordinary variables are upper case X, Y, etc. In the intended interpretation, the variables these stand for classesClass (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
, and the atomic formula
means "class X is an element of class Y". A set is a class that is an element of a class. Small case variables x, y, etc. stand for sets. A proper class is a class that is not a set. Two classes are equinumerousEquinumerosity
In mathematics, two sets are equinumerous if they have the same cardinality, i.e., if there exists a bijection f : A → B for sets A and B. This is usually denoted A \approx B \, or A \sim B....
iff a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
exists between them. A class is infinite iff it is equinumerous with one of its proper subclasses. The axioms of PST are
- (A1) (extensionality) — Classes that have the same elements are the same.
- (A2) (class comprehension) — If
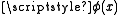is a formula, then there exists a class the elements of which are exactly those sets x that satisfy 
.
-
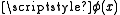- (A3) (axiom of infinity) — There is an infinite set, and all infinite sets are equinumerous.
-
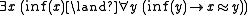
- (inf(x) stands for “x is infinite”;
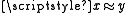abbreviates that x is equinumerous with y.)
-
- (A4) (limitation of size) – A class is a proper class if and only if it s equinumerous with all proper classes.
-
- (pr(X) stands for “X is a proper class”.)
Remarks on the axioms
- Although different kinds of variables are used for classes and sets, the language is not many-sorted; sets are identified with classes having the same extension. Small case variables are used as mere abbreviations for various contexts; e.g.,
- Since the quantification in A2 ranges over classes, i.e.,
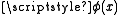is not set-bound, A2 is the comprehension scheme of Morse–Kelley set theoryMorse–Kelley set theoryIn the foundation of mathematics, Morse–Kelley set theory or Kelley–Morse set theory is a first order axiomatic set theory that is closely related to von Neumann–Bernays–Gödel set theory...
, not that of Von Neumann–Bernays–Gödel set theoryVon Neumann–Bernays–Gödel set theoryIn the foundations of mathematics, von Neumann–Bernays–Gödel set theory is an axiomatic set theory that is a conservative extension of the canonical axiomatic set theory ZFC. A statement in the language of ZFC is provable in NBG if and only if it is provable in ZFC. The ontology of NBG includes...
. This extra strength of A2 is employed in the definition of the ordinals (not presented here). - Since there is no axiom of pairingAxiom of pairingIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of pairing is one of the axioms of Zermelo–Fraenkel set theory.- Formal statement :...
, it must be proved that the Kuratowski pair of any two sets exists and is a set. Hence establishing that there exists a one-to-one correspondence between two classes does not assure that they are equinumerous.
Some theorems of PST
1. The Russell class is a proper class. ()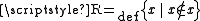
- Proof: This is actually Russell's paradoxRussell's paradoxIn the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...
.
2. The empty class is a set. (
)
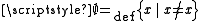- Proof: Suppose (towards a contradiction) that the empty class is a proper class. According to (A4), it is equinumerous with R; that is, R is empty. Let i be an infinite set, and consider the class
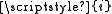. It is not equinumerous with 
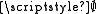, thus it is a set. It is finite, but its single element is infinite, thus it cannot be an element of itself. Therefore, it is an element of R. This contradicts that R is empty.
3. The singleton class of the empty set is a set.
- Proof: Suppose that
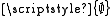is a proper class. Then, according to (A4), every proper class is a singleton. Let i be an infinite set and consider the class 
. It is neither a proper class (because it is not singleton) nor an element of itself (because it is neither empty nor infinite). Thus by definition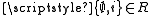 
, so R has at least two elements, 
and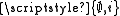 
. This contradicts our assumption that proper classes are singletons.
4. The Russell class is infinite.
- Proof: Let
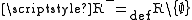. Suppose that this class is a set. Then either 
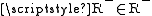or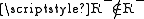 
. In the first case by definition of 
: 
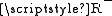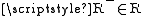and hence 
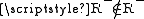, which is a contradiction. In the second case, again by definition of 
: either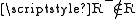 
and hence 
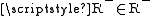, which is a contradiction, or 
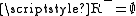. But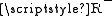 
is not empty, because 
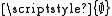is an element of it.
5. Every finite class is a set.
- Proof: Let X be a proper class. According to (A4), there exists an
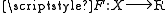such that F is a bijection. This contains a pair 
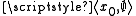, and for each member r of 
, a pair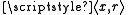 
. Let 
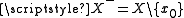and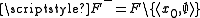 
. According to (A4), both of these classes exist. Now, 
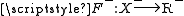is a bijection. Thus, according to (A4), 
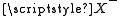is a proper class, too. Clearly, 
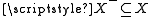and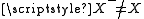 
. Now, another application of (A4) shows that there exists a bijection 
. This proves that X is infinite.
Once the above facts are settled, the following results can be proved:
5. The class V of sets (
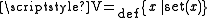) consists of all hereditarily countable sets.6. Every proper class has the cardinality
.
- Proof: Let i be an infinite set. The class
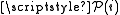has the cardinality 
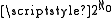. According to (A4), all proper classes have the cardinality 
.
7. The union class of a set is a set.
PST also verifies
- the continuum hypothesisContinuum hypothesisIn mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
- See (5) and (6) above.
- the axiom of replacement
- This is actually part of the axiom of limitation of size.
- the axiom of choice
- Both the class V of sets and the class Ord of ordinals are proper classes (because of Cantor's paradoxCantor's paradoxIn set theory, Cantor's paradox is derivable from the theorem that there is no greatest cardinal number, so that the collection of "infinite sizes" is itself infinite...
and the Burali-Forti paradoxBurali-Forti paradoxIn set theory, a field of mathematics, the Burali-Forti paradox demonstrates that naively constructing "the set of all ordinal numbers" leads to a contradiction and therefore shows an antinomy in a system that allows its construction...
, respectively, therefore there exists a bijection between them, which well-orders the universe.
The theory neither approves nor rejects well-foundedness.
Possible extensions
- Adding the so-called axiom of free construction to PST, any consistent system of set-theoretical axioms will have an inner model in the resulting system.
- It is an unfriendly feature of PST that it cannot handle classes of sets of real numbers or classes of sets of real functions. However, it is not a necessary one. (A3) can be modified various ways to allow for various portions of the usual hierarchy of infinites, with or without supporting the continuum hypothesis. One example is
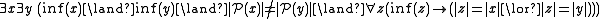
- In this version, the cardinality of an infinite set is either
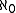or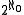 
, and the cardinality of a proper class is 
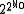(which means that the generalized continuum hypothesis holds.