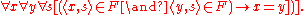Morse–Kelley set theory
Encyclopedia
In the foundation of mathematics, Morse–Kelley set theory (MK) or Kelley–Morse set theory (KM) is a first order axiomatic set theory that is closely related to von Neumann–Bernays–Gödel set theory
(NBG). While von Neumann–Bernays–Gödel set theory restricts the bound variables in the schematic formula appearing in the axiom schema
of Class Comprehension to range over sets alone, Morse–Kelley set theory allows these bound variables to range over proper classes as well as sets.
Morse–Kelley set theory is named after mathematicians John L. Kelley
and Anthony Morse
and was first set out in an appendix to Kelley's text book General Topology (1955), a graduate level introduction to topology
. Kelley himself referred to it as Skolem–Morse set theory, after Thoralf Skolem
. Morse's own version appeared later in his book A Theory of Sets (1965).
While von Neumann–Bernays–Gödel set theory is a conservative extension
of Zermelo–Fraenkel set theory
(ZFC, the canonical set theory) in the sense that a statement in the language of ZFC is provable in NBG if and only if it is provable in ZFC, Morse–Kelley set theory is a proper extension of ZFC. Unlike von Neumann–Bernays–Gödel set theory, where the axiom schema of Class Comprehension can be replaced with finitely many of its instances, Morse–Kelley set theory cannot be finitely axiomatized.
and MK share a common ontology
. The universe of discourse consists of classes. Classes which are members of other classes are called sets. A class which is not a set is a proper class. The primitive atomic sentence
s involve membership or equality.
With the exception of Class Comprehension, the following axioms are the same as those for NBG
, inessential details aside. The symbolic versions of the axioms employ the following notational devices:
Extensionality
: Classes having the same members are the same class.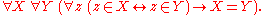
Foundation: Each nonempty class A is disjoint from at least one of its members.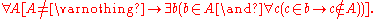
Class Comprehension: Let φ(x) be any formula in the language of MK in which x is a free variable and Y is not free. φ(x) may contain parameters which are either sets or proper classes. More consequentially, the quantified variables in φ(x) may range over all classes and not just over all sets; this is the only way MK differs from NBG
. Then there exists a class
whose members are exactly those sets x such that 
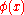comes out true. Formally, if Y is not free in φ: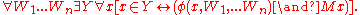
Pairing
: For any sets x and y, there exists a set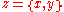
whose members are exactly x and y.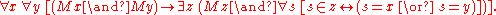
Limitation of Size
: C is a proper class if and only if V
can be mapped one-to-one into C.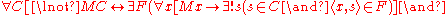
Power set
: Let p be a class whose members are all possible subset
s of the set a. Then p is a set.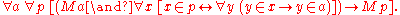
Union
: Let
be the sum class of the set a, namely the union
of all members of a. Then s is a set.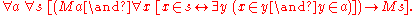
Infinity
: There exists an inductive set
y, meaning that (i) the empty set
is a member of y; (ii) if x is a member of y, then so is
.
Note that p and s in Power Set and Union are universally, not existentially, quantified, as Class Comprehension suffices to establish the existence of p and s. Power Set and Union only serve to establish that p and s cannot be proper classes.
The above axioms are shared with other set theories as follows:
includes urelements. These authors and Mendelson (1997: 287) submit that MK does what we expect of a set theory while being less cumbersome than ZFC
and NBG
.
MK is strictly stronger than ZFC and its conservative extension
NBG, the other well-known set theory with proper classes. In fact, NBG—and hence ZFC—can be proved consistent if MK is. MK's strength stems from its axiom schema of Class Comprehension being impredicative, meaning that φ(x) may contain quantified variables ranging over classes. The quantified variables in NBG's axiom schema of Class Comprehension are restricted to sets; hence Class Comprehension in NBG must be predicative. (Separation with respect to sets is still impredicative in NBG, because the quantifiers in φ(x) may range over all sets.) The NBG axiom schema of Class Comprehension can be replaced with finitely many of its instances; this is not possible in MK. MK is consistent relative to ZFC augmented by an axiom asserting the existence of strongly inaccessible ordinal
s.
The only advantage of the axiom of limitation of size
is that it implies the axiom of global choice
. Limitation of Size does not appear in Rubin (1967), Monk (1980), or Mendelson (1997). Instead, these authors invoke a usual form of the local axiom of choice, and an "axiom of replacement," asserting that if the domain
of a class function is a set, its range
is also a set. Replacement can prove everything that Limitation of Size proves, except prove some form of the axiom of choice.
Limitation of Size
plus I being a set
(hence the universe is nonempty) renders provable the sethood of the empty set; hence no need for an axiom of empty set
. Such an axiom could be added, of course, and minor perturbations of the above axioms would necessitate this addition. The set I is not identified with the limit ordinal
as I could be a set larger than 
In this case, the existence of 
would follow from either form of Limitation of Size.
The class of von Neumann ordinals can be well-order
ed. It cannot be a set (under pain of paradox); hence that class is a proper class, and all proper classes have the same size as V. Hence V too can be well-ordered.
MK can be confused with second-order ZFC, ZFC with second-order logic
(representing second-order objects in set rather than predicate language) as its background logic. The language of second-order ZFC is similar to that of MK (although a set and a class having the same extension can no longer be identified), and their syntactical
resources for practical proof are almost identical (and are identical if MK includes the strong form of Limitation of Size). But the semantics
of second-order ZFC are quite different from those of MK. For example, if MK is consistent then it has a countable first-order model, while second-order ZFC has no countable models.
of ZFC
and the von Neumann universe
. Let the inaccessible cardinal
κ be a member of V. Also let Def(X) denote the Δ0 definable subset
s of X (see constructible universe
). Then:
class comprehension was Quine's ML
, that built on New Foundations
rather than on ZFC
. Impredicative
class comprehension was also proposed in Mostowski
(1951) and Lewis
(1991).
Notations appearing below and now well-known are not defined. Peculiarities of Kelley's notation include:
Definition: x is a set (and hence not a proper class) if, for some y,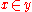
.
I. Extent: For each x and each y, x=y if and only if for each z,
when and only when 
Identical to Extensionality above. I would be identical to the axiom of extensionality
in ZFC, except that the scope of I includes proper classes as well as sets.
II. Classification (schema): An axiom results if in
'α' and 'β' are replaced by variables, ' A ' by a formula Æ, and ' B ' by the formula obtained from Æ by replacing each occurrence of the variable which replaced α by the variable which replaced β.
Develop: Boolean algebra of sets
. Existence of the null class
and of the universal class
V.
III. Subsets: If x is a set, there exists a set y such that for each z, if
, then 
The import of III is that of Power Set above. Sketch of the proof of Power Set from III: for any class z which is a subclass of the set x, the class z is a member of the set y whose existence III asserts. Hence z is a set.
Develop: V is not a set. Existence of singletons. Separation provable.
IV. Union: If x and y are both sets, then
is a set.
The import of IV is that of Pairing above. Sketch of the proof of Pairing from IV: the singleton
of a set x is a set because it is a subclass of the power set of x (by two applications of III). Then IV implies that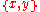 
is a set if x and y are sets.
Develop: Unordered and ordered pair
s, relations
, functions, domain
, range
, function composition
.
V. Substitution: If f is a [class] function and domain f is a set, then range f is a set.
The import of V is that of the axiom schema of replacement
in NBG
and ZFC.
VI. Amalgamation: If x is a set, then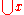
is a set.
The import of VI is that of Union above. V and VI may be combined into one axiom.
Develop: Cartesian product
, injection
, surjection, bijection
, order theory
.
VII. Regularity: If
there is a member y of x such that 
The import of VII is that of Foundation above.
Develop: Ordinal number
s, transfinite induction
.
VIII. Infinity: There exists a set y, such that
and 
whenever 
This axiom, or equivalents thereto, are included in ZFC and NBG. VIII asserts the unconditional existence of two sets, the infinite inductive set
y, and the null set
is a set simply because it is a member of y. Up to this point, everything that has been proved to exist is a class, and Kelley's discussion of sets was entirely hypothetical.
Develop: Natural number
s, N is a set, Peano axioms
, integer
s, rational number
s, real number
s.
Definition: c is a choice function if c is a function and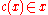
for each member x of domain c.
IX. Choice: There exists a choice function c whose domain is
.
IX is very similar to the axiom of global choice
derivable from Limitation of Size above.
Develop: Equivalents of the axiom of choice. As is the case with ZFC
, the development of the cardinal number
s requires some form of Choice.
If the scope of all quantified variables in the above axioms is restricted to sets, all axioms except III and the schema IV are ZFC axioms. IV is provable in ZFC. Hence the Kelley treatment of MK makes very clear that all that distinguishes MK from ZFC are variables ranging over proper classes as well as sets, and the Classification schema.
Von Neumann–Bernays–Gödel set theory
In the foundations of mathematics, von Neumann–Bernays–Gödel set theory is an axiomatic set theory that is a conservative extension of the canonical axiomatic set theory ZFC. A statement in the language of ZFC is provable in NBG if and only if it is provable in ZFC. The ontology of NBG includes...
(NBG). While von Neumann–Bernays–Gödel set theory restricts the bound variables in the schematic formula appearing in the axiom schema
Axiom schema
In mathematical logic, an axiom schema generalizes the notion of axiom.An axiom schema is a formula in the language of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which...
of Class Comprehension to range over sets alone, Morse–Kelley set theory allows these bound variables to range over proper classes as well as sets.
Morse–Kelley set theory is named after mathematicians John L. Kelley
John L. Kelley
John Leroy Kelley was an American mathematician at University of California, Berkeley who worked in general topology and functional analysis....
and Anthony Morse
Anthony Morse
Anthony Perry Morse was an American mathematician who worked in both analysis, especially measure theory, and in the foundations of mathematics. He is best known as the co-creator, together with John L. Kelley, of Morse–Kelley set theory. This theory first appeared in print in General...
and was first set out in an appendix to Kelley's text book General Topology (1955), a graduate level introduction to topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. Kelley himself referred to it as Skolem–Morse set theory, after Thoralf Skolem
Thoralf Skolem
Thoralf Albert Skolem was a Norwegian mathematician known mainly for his work on mathematical logic and set theory.-Life:...
. Morse's own version appeared later in his book A Theory of Sets (1965).
While von Neumann–Bernays–Gödel set theory is a conservative extension
Conservative extension
In mathematical logic, a logical theory T_2 is a conservative extension of a theory T_1 if the language of T_2 extends the language of T_1; every theorem of T_1 is a theorem of T_2; and any theorem of T_2 which is in the language of T_1 is already a theorem of T_1.More generally, if Γ is a set of...
of Zermelo–Fraenkel set theory
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
(ZFC, the canonical set theory) in the sense that a statement in the language of ZFC is provable in NBG if and only if it is provable in ZFC, Morse–Kelley set theory is a proper extension of ZFC. Unlike von Neumann–Bernays–Gödel set theory, where the axiom schema of Class Comprehension can be replaced with finitely many of its instances, Morse–Kelley set theory cannot be finitely axiomatized.
MK axioms and ontology
NBGVon Neumann–Bernays–Gödel set theory
In the foundations of mathematics, von Neumann–Bernays–Gödel set theory is an axiomatic set theory that is a conservative extension of the canonical axiomatic set theory ZFC. A statement in the language of ZFC is provable in NBG if and only if it is provable in ZFC. The ontology of NBG includes...
and MK share a common ontology
Ontology
Ontology is the philosophical study of the nature of being, existence or reality as such, as well as the basic categories of being and their relations...
. The universe of discourse consists of classes. Classes which are members of other classes are called sets. A class which is not a set is a proper class. The primitive atomic sentence
Atomic sentence
In logic, an atomic sentence is a type of declarative sentence which is either true or false and which cannot be broken down into other simpler sentences...
s involve membership or equality.
With the exception of Class Comprehension, the following axioms are the same as those for NBG
Von Neumann–Bernays–Gödel set theory
In the foundations of mathematics, von Neumann–Bernays–Gödel set theory is an axiomatic set theory that is a conservative extension of the canonical axiomatic set theory ZFC. A statement in the language of ZFC is provable in NBG if and only if it is provable in ZFC. The ontology of NBG includes...
, inessential details aside. The symbolic versions of the axioms employ the following notational devices:
- The upper case letters other than M, appearing in Extensionality, Class Comprehension, and Foundation, denote variables ranging over classes. A lower case letter denotes a variable that cannot be a proper class, because it appears to the left of an ∈. As MK is a one-sorted theory, this notational convention is only mnemonicMnemonicA mnemonic , or mnemonic device, is any learning technique that aids memory. To improve long term memory, mnemonic systems are used to make memorization easier. Commonly encountered mnemonics are often verbal, such as a very short poem or a special word used to help a person remember something,...
; - The monadicUnary operationIn mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
predicate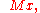
whose intended reading is "'the class x is a set," abbreviates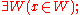 
- The empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
is defined by 
- The class V, the universal classUniverse (mathematics)In mathematics, and particularly in set theory and the foundations of mathematics, a universe is a class that contains all the entities one wishes to consider in a given situation...
having all possible sets as members, is defined by
V is also the Von Neumann universeVon Neumann universeIn set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted V, is the class of hereditary well-founded sets...
.
Extensionality
Axiom of extensionality
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
: Classes having the same members are the same class.
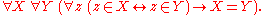
- Note that a set and a class having the same extension are identical. Hence MK is not a two-sorted theory, appearances to the contrary notwithstanding.
Foundation: Each nonempty class A is disjoint from at least one of its members.
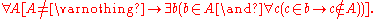
Class Comprehension: Let φ(x) be any formula in the language of MK in which x is a free variable and Y is not free. φ(x) may contain parameters which are either sets or proper classes. More consequentially, the quantified variables in φ(x) may range over all classes and not just over all sets; this is the only way MK differs from NBG
Von Neumann–Bernays–Gödel set theory
In the foundations of mathematics, von Neumann–Bernays–Gödel set theory is an axiomatic set theory that is a conservative extension of the canonical axiomatic set theory ZFC. A statement in the language of ZFC is provable in NBG if and only if it is provable in ZFC. The ontology of NBG includes...
. Then there exists a class
whose members are exactly those sets x such that 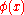comes out true. Formally, if Y is not free in φ: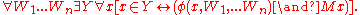Pairing
Axiom of pairing
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of pairing is one of the axioms of Zermelo–Fraenkel set theory.- Formal statement :...
: For any sets x and y, there exists a set
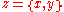whose members are exactly x and y.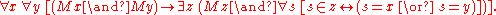- Pairing licenses the unordered pair in terms of which the ordered pairOrdered pairIn mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
,
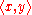, may be defined in the usual way, as 
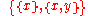. With ordered pairs in hand, Class Comprehension enables defining relationsRelation (mathematics)In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
and functions on sets as sets of ordered pairs, making possible the next axiom:
Limitation of Size
Axiom of limitation of size
In class theories, the axiom of limitation of size says that for any class C, C is a proper class, that is a class which is not a set , if and only if it can be mapped onto the class V of all sets....
: C is a proper class if and only if V
Von Neumann universe
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted V, is the class of hereditary well-founded sets...
can be mapped one-to-one into C.
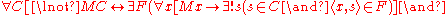
- The formal version of this axiom resembles the axiom schema of replacementAxiom schema of replacementIn set theory, the axiom schema of replacement is a schema of axioms in Zermelo–Fraenkel set theory that asserts that the image of any set under any definable mapping is also a set...
, and embodies the class function F. The next section explains how Limitation of Size is stronger than the usual forms of the axiom of choice.
Power set
Axiom of power set
In mathematics, the axiom of power set is one of the Zermelo–Fraenkel axioms of axiomatic set theory.In the formal language of the Zermelo–Fraenkel axioms, the axiom reads:...
: Let p be a class whose members are all possible subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of the set a. Then p is a set.
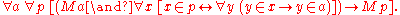
Union
Axiom of union
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of union is one of the axioms of Zermelo-Fraenkel set theory, stating that, for any set x there is a set y whose elements are precisely the elements of the elements of x...
: Let
be the sum class of the set a, namely the unionUnion (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of all members of a. Then s is a set.
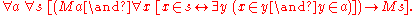
Infinity
Axiom of infinity
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
: There exists an inductive set
Inductive set
In descriptive set theory, an inductive set of real numbers is one that can be defined as the least fixed point of a monotone operation definable by a positive Σ1n formula, for some natural number n, together with a real parameter.The inductive sets form a boldface pointclass; that is, they...
y, meaning that (i) the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
is a member of y; (ii) if x is a member of y, then so is
.Note that p and s in Power Set and Union are universally, not existentially, quantified, as Class Comprehension suffices to establish the existence of p and s. Power Set and Union only serve to establish that p and s cannot be proper classes.
The above axioms are shared with other set theories as follows:
- ZFCZermelo–Fraenkel set theoryIn mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
and NBGVon Neumann–Bernays–Gödel set theoryIn the foundations of mathematics, von Neumann–Bernays–Gödel set theory is an axiomatic set theory that is a conservative extension of the canonical axiomatic set theory ZFC. A statement in the language of ZFC is provable in NBG if and only if it is provable in ZFC. The ontology of NBG includes...
: Pairing, Power Set, Union, Infinity; - NBGVon Neumann–Bernays–Gödel set theoryIn the foundations of mathematics, von Neumann–Bernays–Gödel set theory is an axiomatic set theory that is a conservative extension of the canonical axiomatic set theory ZFC. A statement in the language of ZFC is provable in NBG if and only if it is provable in ZFC. The ontology of NBG includes...
(and ZFC, if quantified variables were restricted to sets): Extensionality, Foundation; - NBGVon Neumann–Bernays–Gödel set theoryIn the foundations of mathematics, von Neumann–Bernays–Gödel set theory is an axiomatic set theory that is a conservative extension of the canonical axiomatic set theory ZFC. A statement in the language of ZFC is provable in NBG if and only if it is provable in ZFC. The ontology of NBG includes...
: Limitation of Size; - MLNew FoundationsIn mathematical logic, New Foundations is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name...
: Extensionality, Class Comprehension (in NFNew FoundationsIn mathematical logic, New Foundations is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name...
, comprehension is restricted to stratified formulas).
Discussion
Monk (1980) and Rubin (1967) are set theory texts built around MK; Rubin's ontologyOntology
Ontology is the philosophical study of the nature of being, existence or reality as such, as well as the basic categories of being and their relations...
includes urelements. These authors and Mendelson (1997: 287) submit that MK does what we expect of a set theory while being less cumbersome than ZFC
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
and NBG
Von Neumann–Bernays–Gödel set theory
In the foundations of mathematics, von Neumann–Bernays–Gödel set theory is an axiomatic set theory that is a conservative extension of the canonical axiomatic set theory ZFC. A statement in the language of ZFC is provable in NBG if and only if it is provable in ZFC. The ontology of NBG includes...
.
MK is strictly stronger than ZFC and its conservative extension
Conservative extension
In mathematical logic, a logical theory T_2 is a conservative extension of a theory T_1 if the language of T_2 extends the language of T_1; every theorem of T_1 is a theorem of T_2; and any theorem of T_2 which is in the language of T_1 is already a theorem of T_1.More generally, if Γ is a set of...
NBG, the other well-known set theory with proper classes. In fact, NBG—and hence ZFC—can be proved consistent if MK is. MK's strength stems from its axiom schema of Class Comprehension being impredicative, meaning that φ(x) may contain quantified variables ranging over classes. The quantified variables in NBG's axiom schema of Class Comprehension are restricted to sets; hence Class Comprehension in NBG must be predicative. (Separation with respect to sets is still impredicative in NBG, because the quantifiers in φ(x) may range over all sets.) The NBG axiom schema of Class Comprehension can be replaced with finitely many of its instances; this is not possible in MK. MK is consistent relative to ZFC augmented by an axiom asserting the existence of strongly inaccessible ordinal
Inaccessible cardinal
In set theory, an uncountable regular cardinal number is called weakly inaccessible if it is a weak limit cardinal, and strongly inaccessible, or just inaccessible, if it is a strong limit cardinal. Some authors do not require weakly and strongly inaccessible cardinals to be uncountable...
s.
The only advantage of the axiom of limitation of size
Axiom of limitation of size
In class theories, the axiom of limitation of size says that for any class C, C is a proper class, that is a class which is not a set , if and only if it can be mapped onto the class V of all sets....
is that it implies the axiom of global choice
Axiom of global choice
In class theories, the axiom of global choice is a stronger variant of the axiom of choice which applies to proper classes as well as sets.- Statement :The axiom can be expressed in various ways which are equivalent:...
. Limitation of Size does not appear in Rubin (1967), Monk (1980), or Mendelson (1997). Instead, these authors invoke a usual form of the local axiom of choice, and an "axiom of replacement," asserting that if the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of a class function is a set, its range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
is also a set. Replacement can prove everything that Limitation of Size proves, except prove some form of the axiom of choice.
Limitation of Size
Axiom of limitation of size
In class theories, the axiom of limitation of size says that for any class C, C is a proper class, that is a class which is not a set , if and only if it can be mapped onto the class V of all sets....
plus I being a set
Axiom of infinity
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
(hence the universe is nonempty) renders provable the sethood of the empty set; hence no need for an axiom of empty set
Axiom of empty set
In axiomatic set theory, the axiom of empty set is an axiom of Zermelo–Fraenkel set theory, the fragment thereof Burgess calls ST, and Kripke–Platek set theory.- Formal statement :...
. Such an axiom could be added, of course, and minor perturbations of the above axioms would necessitate this addition. The set I is not identified with the limit ordinal
as I could be a set larger than In this case, the existence of would follow from either form of Limitation of Size.The class of von Neumann ordinals can be well-order
Well-order
In mathematics, a well-order relation on a set S is a strict total order on S with the property that every non-empty subset of S has a least element in this ordering. Equivalently, a well-ordering is a well-founded strict total order...
ed. It cannot be a set (under pain of paradox); hence that class is a proper class, and all proper classes have the same size as V. Hence V too can be well-ordered.
MK can be confused with second-order ZFC, ZFC with second-order logic
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
(representing second-order objects in set rather than predicate language) as its background logic. The language of second-order ZFC is similar to that of MK (although a set and a class having the same extension can no longer be identified), and their syntactical
Syntax
In linguistics, syntax is the study of the principles and rules for constructing phrases and sentences in natural languages....
resources for practical proof are almost identical (and are identical if MK includes the strong form of Limitation of Size). But the semantics
Semantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
of second-order ZFC are quite different from those of MK. For example, if MK is consistent then it has a countable first-order model, while second-order ZFC has no countable models.
Model theory
ZFC, NBG, and MK each have models describable in terms of V, the standard modelInner model
In mathematical logic, suppose T is a theory in the languageL = \langle \in \rangleof set theory.If M is a model of L describing a set theory and N is a class of M such that \langle N, \in_M, \ldots \rangle...
of ZFC
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
and the von Neumann universe
Von Neumann universe
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted V, is the class of hereditary well-founded sets...
. Let the inaccessible cardinal
Inaccessible cardinal
In set theory, an uncountable regular cardinal number is called weakly inaccessible if it is a weak limit cardinal, and strongly inaccessible, or just inaccessible, if it is a strong limit cardinal. Some authors do not require weakly and strongly inaccessible cardinals to be uncountable...
κ be a member of V. Also let Def(X) denote the Δ0 definable subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of X (see constructible universe
Constructible universe
In mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...
). Then:
- Vκ is an intended modelIntended interpretationOne who constructs a syntactical system usually has in mind from the outset some interpretation of this system. While this intended interpretation can have no explicit indication in the syntactical rules - since these rules must be strictly formal - the author's intention respecting...
of ZFCZermelo–Fraenkel set theoryIn mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
; - Def(Vκ) is an intended model of NBGVon Neumann–Bernays–Gödel set theoryIn the foundations of mathematics, von Neumann–Bernays–Gödel set theory is an axiomatic set theory that is a conservative extension of the canonical axiomatic set theory ZFC. A statement in the language of ZFC is provable in NBG if and only if it is provable in ZFC. The ontology of NBG includes...
; - Vκ+1, the power set of Vκ, is an intended model of MK.
History
MK was first set out in an appendix to J. L. Kelley's (1955) General Topology, using the axioms given in the next section. The system of Anthony Morse's (1965) A Theory of Sets is equivalent to Kelley's, but formulated in an idiosyncratic formal language rather than, as is done here, in standard first order logic. The first set theory to include impredicativeImpredicative
In mathematics and logic, impredicativity is the property of a self-referencing definition. More precisely, a definition is said to be impredicative if it invokes the set being defined, or another set which contains the thing being defined.Russell's paradox is a famous example of an impredicative...
class comprehension was Quine's ML
New Foundations
In mathematical logic, New Foundations is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name...
, that built on New Foundations
New Foundations
In mathematical logic, New Foundations is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name...
rather than on ZFC
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
. Impredicative
Impredicative
In mathematics and logic, impredicativity is the property of a self-referencing definition. More precisely, a definition is said to be impredicative if it invokes the set being defined, or another set which contains the thing being defined.Russell's paradox is a famous example of an impredicative...
class comprehension was also proposed in Mostowski
Mostowski
Mostowski, Mostowska is surname of:* Mostowski Palace , an 18th-century palace in Warsaw* Andrzej Mostowski , a Polish mathematician** Mostowski collapse lemma, in mathematical logic** Ehrenfeucht–Mostowski theorem, in model theory...
(1951) and Lewis
David Kellogg Lewis
David Kellogg Lewis was an American philosopher. Lewis taught briefly at UCLA and then at Princeton from 1970 until his death. He is also closely associated with Australia, whose philosophical community he visited almost annually for more than thirty years...
(1991).
The axioms in Kelley's General topology
The axioms and definitions in this section are, but for a few inessential details, taken from the Appendix to Kelley (1955). The explanatory remarks below are not his. The Appendix states 181 theorems and definitions, and warrants careful reading as an abbreviated exposition of axiomatic set theory by a working mathematician of the first rank. Kelley introduced his axioms gradually, as needed to develop the topics listed after each instance of Develop below.Notations appearing below and now well-known are not defined. Peculiarities of Kelley's notation include:
- He did not distinguish variables ranging over classes from those ranging over sets;
- domain f and range f denote the domain and range of the function f; this peculiarity has been carefully respected below;
- His primitive logical language includes class abstracts of the form
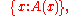"the class of all sets x satisfying A(x)."
Definition: x is a set (and hence not a proper class) if, for some y,
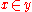.I. Extent: For each x and each y, x=y if and only if for each z,
when and only when Identical to Extensionality above. I would be identical to the axiom of extensionality
Axiom of extensionality
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
in ZFC, except that the scope of I includes proper classes as well as sets.
II. Classification (schema): An axiom results if in
- For each
, 
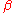if and only if 
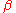is a set and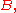 
'α' and 'β' are replaced by variables, ' A ' by a formula Æ, and ' B ' by the formula obtained from Æ by replacing each occurrence of the variable which replaced α by the variable which replaced β.
Develop: Boolean algebra of sets
Algebra of sets
The algebra of sets develops and describes the basic properties and laws of sets, the set-theoretic operations of union, intersection, and complementation and the relations of set equality and set inclusion...
. Existence of the null class
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
and of the universal class
Universal class
Universal class is a category derived from the philosophy of Hegel, redefined and popularized by Karl Marx. In Marxism it denotes that class of people within a stratified society for which, at a given point in history, self interested action coincides with the needs of humanity as a...
V.
III. Subsets: If x is a set, there exists a set y such that for each z, if
, then The import of III is that of Power Set above. Sketch of the proof of Power Set from III: for any class z which is a subclass of the set x, the class z is a member of the set y whose existence III asserts. Hence z is a set.
Develop: V is not a set. Existence of singletons. Separation provable.
IV. Union: If x and y are both sets, then
is a set.The import of IV is that of Pairing above. Sketch of the proof of Pairing from IV: the singleton
of a set x is a set because it is a subclass of the power set of x (by two applications of III). Then IV implies that 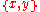is a set if x and y are sets.Develop: Unordered and ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
s, relations
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
, functions, domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
, range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
, function composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
.
V. Substitution: If f is a [class] function and domain f is a set, then range f is a set.
The import of V is that of the axiom schema of replacement
Axiom schema of replacement
In set theory, the axiom schema of replacement is a schema of axioms in Zermelo–Fraenkel set theory that asserts that the image of any set under any definable mapping is also a set...
in NBG
NBG
NBG may refer to:*National Bank of Georgia*National Bank of Greece*Naus-Bruisma-Geruko, NBG Industrial BV*The IATA airport identifier for Naval Air Station Joint Reserve Base New Orleans*The von Neumann–Bernays–Gödel set theory*The Nordic Battle Group...
and ZFC.
VI. Amalgamation: If x is a set, then
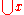is a set.The import of VI is that of Union above. V and VI may be combined into one axiom.
Develop: Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
, injection
Injection
Injection or Injected may refer to:* Injection , insertion of liquid into the body with a syringe* Injective function in mathematics, a function mapping distinct arguments to distinct values...
, surjection, bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
, order theory
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
.
VII. Regularity: If
there is a member y of x such that The import of VII is that of Foundation above.
Develop: Ordinal number
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
s, transfinite induction
Transfinite induction
Transfinite induction is an extension of mathematical induction to well-ordered sets, for instance to sets of ordinal numbers or cardinal numbers.- Transfinite induction :Let P be a property defined for all ordinals α...
.
VIII. Infinity: There exists a set y, such that
and whenever This axiom, or equivalents thereto, are included in ZFC and NBG. VIII asserts the unconditional existence of two sets, the infinite inductive set
Inductive set
In descriptive set theory, an inductive set of real numbers is one that can be defined as the least fixed point of a monotone operation definable by a positive Σ1n formula, for some natural number n, together with a real parameter.The inductive sets form a boldface pointclass; that is, they...
y, and the null set
is a set simply because it is a member of y. Up to this point, everything that has been proved to exist is a class, and Kelley's discussion of sets was entirely hypothetical.Develop: Natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s, N is a set, Peano axioms
Peano axioms
In mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are a set of axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano...
, integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s, real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s.
Definition: c is a choice function if c is a function and
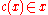for each member x of domain c.IX. Choice: There exists a choice function c whose domain is
.IX is very similar to the axiom of global choice
Axiom of global choice
In class theories, the axiom of global choice is a stronger variant of the axiom of choice which applies to proper classes as well as sets.- Statement :The axiom can be expressed in various ways which are equivalent:...
derivable from Limitation of Size above.
Develop: Equivalents of the axiom of choice. As is the case with ZFC
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
, the development of the cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s requires some form of Choice.
If the scope of all quantified variables in the above axioms is restricted to sets, all axioms except III and the schema IV are ZFC axioms. IV is provable in ZFC. Hence the Kelley treatment of MK makes very clear that all that distinguishes MK from ZFC are variables ranging over proper classes as well as sets, and the Classification schema.