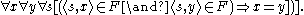Axiom of limitation of size
Encyclopedia
In class theories, the axiom of limitation of size says that for any class C, C is a proper class, that is a class which is not a set (an element of other classes), if and only if it can be mapped onto the class V
of all sets.

This axiom is due to John von Neumann
. It implies the axiom schema of specification
, axiom schema of replacement
, axiom of global choice
, and even, as noticed later by Azriel Levy
, axiom of union
at one stroke. The axiom of limitation of size implies the axiom of global choice because the class of ordinals is not a set, so there is a surjection from the ordinals to the universe, thus an injection from the universe to the ordinals, that is, the universe of sets is well-order
ed.
Together the axiom of replacement and the axiom of global choice
(with the other axioms of von Neumann–Bernays–Gödel set theory
) imply this axiom. This axiom can then replace replacement, global choice, specification and union in von Neumann–Bernays–Gödel or Morse–Kelley set theory
.
It can be shown that a class is a proper class if and only if it is equinumerous to V, but von Neumann's axiom does not capture all of the "limitation of size
doctrine", because the axiom of power set
is not a consequence of it. Later expositions of class theories (Bernays
, Gödel
, Kelley
, ...) generally use replacement and a form of axiom of choice rather than axiom of limitation of size.
Von Neumann universe
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted V, is the class of hereditary well-founded sets...
of all sets.

This axiom is due to John von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
. It implies the axiom schema of specification
Axiom schema of specification
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom schema of specification, axiom schema of separation, subset axiom scheme or axiom schema of restricted comprehension, is a schema of axioms in Zermelo-Fraenkel set theory...
, axiom schema of replacement
Axiom schema of replacement
In set theory, the axiom schema of replacement is a schema of axioms in Zermelo–Fraenkel set theory that asserts that the image of any set under any definable mapping is also a set...
, axiom of global choice
Axiom of global choice
In class theories, the axiom of global choice is a stronger variant of the axiom of choice which applies to proper classes as well as sets.- Statement :The axiom can be expressed in various ways which are equivalent:...
, and even, as noticed later by Azriel Levy
Azriel Levy
Azriel Levy is an Israeli mathematician, logician, and a professor emeritus at the Hebrew University of Jerusalem....
, axiom of union
Axiom of union
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of union is one of the axioms of Zermelo-Fraenkel set theory, stating that, for any set x there is a set y whose elements are precisely the elements of the elements of x...
at one stroke. The axiom of limitation of size implies the axiom of global choice because the class of ordinals is not a set, so there is a surjection from the ordinals to the universe, thus an injection from the universe to the ordinals, that is, the universe of sets is well-order
Well-order
In mathematics, a well-order relation on a set S is a strict total order on S with the property that every non-empty subset of S has a least element in this ordering. Equivalently, a well-ordering is a well-founded strict total order...
ed.
Together the axiom of replacement and the axiom of global choice
Axiom of global choice
In class theories, the axiom of global choice is a stronger variant of the axiom of choice which applies to proper classes as well as sets.- Statement :The axiom can be expressed in various ways which are equivalent:...
(with the other axioms of von Neumann–Bernays–Gödel set theory
Von Neumann–Bernays–Gödel set theory
In the foundations of mathematics, von Neumann–Bernays–Gödel set theory is an axiomatic set theory that is a conservative extension of the canonical axiomatic set theory ZFC. A statement in the language of ZFC is provable in NBG if and only if it is provable in ZFC. The ontology of NBG includes...
) imply this axiom. This axiom can then replace replacement, global choice, specification and union in von Neumann–Bernays–Gödel or Morse–Kelley set theory
Morse–Kelley set theory
In the foundation of mathematics, Morse–Kelley set theory or Kelley–Morse set theory is a first order axiomatic set theory that is closely related to von Neumann–Bernays–Gödel set theory...
.
It can be shown that a class is a proper class if and only if it is equinumerous to V, but von Neumann's axiom does not capture all of the "limitation of size
Limitation of size
In the philosophy of mathematics, specifically the philosophical foundations of set theory, limitation of size is a concept developed by Philip Jourdain and/or Georg Cantor to avoid Cantor's paradox. It identifies certain "inconsistent multiplicities", in Cantor's terminology, that cannot be sets...
doctrine", because the axiom of power set
Axiom of power set
In mathematics, the axiom of power set is one of the Zermelo–Fraenkel axioms of axiomatic set theory.In the formal language of the Zermelo–Fraenkel axioms, the axiom reads:...
is not a consequence of it. Later expositions of class theories (Bernays
Paul Bernays
Paul Isaac Bernays was a Swiss mathematician, who made significant contributions to mathematical logic, axiomatic set theory, and the philosophy of mathematics. He was an assistant to, and close collaborator of, David Hilbert.-Biography:Bernays spent his childhood in Berlin. Bernays attended the...
, Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
, Kelley
John L. Kelley
John Leroy Kelley was an American mathematician at University of California, Berkeley who worked in general topology and functional analysis....
, ...) generally use replacement and a form of axiom of choice rather than axiom of limitation of size.
See also
- Axiom of global choiceAxiom of global choiceIn class theories, the axiom of global choice is a stronger variant of the axiom of choice which applies to proper classes as well as sets.- Statement :The axiom can be expressed in various ways which are equivalent:...
- Limitation of sizeLimitation of sizeIn the philosophy of mathematics, specifically the philosophical foundations of set theory, limitation of size is a concept developed by Philip Jourdain and/or Georg Cantor to avoid Cantor's paradox. It identifies certain "inconsistent multiplicities", in Cantor's terminology, that cannot be sets...
- Von Neumann–Bernays–Gödel set theoryVon Neumann–Bernays–Gödel set theoryIn the foundations of mathematics, von Neumann–Bernays–Gödel set theory is an axiomatic set theory that is a conservative extension of the canonical axiomatic set theory ZFC. A statement in the language of ZFC is provable in NBG if and only if it is provable in ZFC. The ontology of NBG includes...
- Morse–Kelley set theoryMorse–Kelley set theoryIn the foundation of mathematics, Morse–Kelley set theory or Kelley–Morse set theory is a first order axiomatic set theory that is closely related to von Neumann–Bernays–Gödel set theory...