
Axiom schema of specification
Encyclopedia
In axiomatic set theory and the branches of logic
, mathematics
, and computer science
that use it, the axiom schema of specification, axiom schema of separation, subset axiom scheme or axiom schema of restricted comprehension, is a schema of axiom
s in Zermelo-Fraenkel set theory. It is also called the axiom schema of comprehension, although that term is also used for unrestricted comprehension, discussed below. Essentially, it says that any definable subclass of a set is a set.
among x, w1, ... , wn, A. So B is not free in φ. In the formal language of set theory, the axiom schema is:
or in words:
Note that there is one axiom for every such predicate φ; thus, this is an axiom schema
.
To understand this axiom schema, note that the set B must be a subset
of A. Thus, what the axiom schema is really saying is that, given a set A and a predicate P, we can find a subset B of A whose members are precisely the members of A that satisfy P. By the axiom of extensionality
this set is unique. We usually denote this set using set-builder notation
as {C ∈ A : P(C)}. Thus the essence of the axiom is:
The axiom schema of specification is characteristic of systems of axiomatic set theory related to the usual set theory ZFC, but does not usually appear in radically different systems of alternative set theory
. For example, New Foundations
and positive set theory use different restrictions of the axiom of comprehension of naive set theory
. The Alternative Set Theory
of Vopenka makes a specific point of allowing proper subclasses of sets, called semiset
s. Even in systems related to ZFC, this scheme is sometimes restricted to formulas with bounded quantifiers, as in Kripke–Platek set theory with urelements
.
.
First, recall this axiom schema:

for any functional predicate
F in one variable
that doesn't use the symbols A, B, C or D.
Given a suitable predicate P for the axiom of specification, define the mapping F by F(D) = D if P(D) is true and F(D) = E if P(D) is false, where E is any member of A such that P(E) is true.
Then the set B guaranteed by the axiom of replacement is precisely the set B required for the axiom of specification. The only problem is if no such E exists. But in this case, the set B required for the axiom of separation is the empty set
, so the axiom of separation follows from the axiom of replacement together with the axiom of empty set
.
For this reason, the axiom schema of separation is often left out of modern lists of the Zermelo-Fraenkel axioms. However, it's still important for historical considerations, and for comparison with alternative axiomatizations of set theory, as can be seen for example in the following sections.
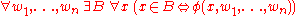
that is:
This set B is again unique, and is usually denoted as {x : φ(x, w_1, ... w_n)}.
This axiom schema was tacitly used in the early days of naive set theory
, before a strict axiomatization was adopted. Unfortunately, it leads directly to Russell's paradox
by taking φ(x) to be ¬(x∈x) (i.e., the property that set x is not a member of itself). Therefore, no useful axiomatization of set theory can use unrestricted comprehension, at least not with classical logic
.
Accepting only the axiom schema of specification was the beginning of axiomatic set theory. Most of the other Zermelo-Fraenkel axioms (but not the axiom of extensionality
or the axiom of regularity
) then became necessary to make up for some of what was lost by changing the axiom schema of comprehension to the axiom schema of specification – each of these axioms states that a certain set exists, and defines that set by giving a predicate for its members to satisfy, i.e. it is a special case of the axiom schema of comprehension.
.
A class C is a set if and only if it belongs to some class E.
In this theory, there is a theorem
schema that reads:

that is:
This theorem schema is itself a restricted form of comprehension, which avoids Russell's paradox because of the requirement that C be a set.
Then specification for sets themselves can be written as a single axiom:
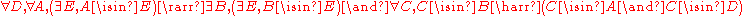
that is:
or even more simply:
In this axiom, the predicate P is replaced by the class D, which can be quantified over.
language where we can quantify over predicates, the axiom schema of specification becomes a simple axiom. This is much the same trick as was used in the NBG axioms of the previous section, where the predicate was replaced by a class that was then quantified over.
In second-order logic
and higher-order logic
with higher-order semantics, the axiom of specification is a logical validity and does not need to be explicitly included in a theory.
approach to set theory pioneered by W.V.O. Quine, the axiom of comprehension for a given predicate takes the unrestricted form, but the predicates that may be used in the schema are themselves restricted.
The predicate (C is not in C) is forbidden, because the same symbol C appears on both sides of the membership symbol (and so at different "relative types"); thus, Russell's paradox is avoided.
However, by taking P(C) to be (C = C), which is allowed, we can form a set of all sets. For details, see stratification
.
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
that use it, the axiom schema of specification, axiom schema of separation, subset axiom scheme or axiom schema of restricted comprehension, is a schema of axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s in Zermelo-Fraenkel set theory. It is also called the axiom schema of comprehension, although that term is also used for unrestricted comprehension, discussed below. Essentially, it says that any definable subclass of a set is a set.
Statement
One instance of the schema is included for each formula φ in the language of set theory with free variablesVariable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
among x, w1, ... , wn, A. So B is not free in φ. In the formal language of set theory, the axiom schema is:

or in words:
- Given any set A, there isExistential quantificationIn predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
a set B such that, given any set x, x is a member of B if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
x is a member of A andLogical conjunctionIn logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
φ holds for x.
Note that there is one axiom for every such predicate φ; thus, this is an axiom schema
Axiom schema
In mathematical logic, an axiom schema generalizes the notion of axiom.An axiom schema is a formula in the language of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which...
.
To understand this axiom schema, note that the set B must be a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of A. Thus, what the axiom schema is really saying is that, given a set A and a predicate P, we can find a subset B of A whose members are precisely the members of A that satisfy P. By the axiom of extensionality
Axiom of extensionality
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
this set is unique. We usually denote this set using set-builder notation
Set-builder notation
In set theory and its applications to logic, mathematics, and computer science, set-builder notation is a mathematical notation for describing a set by stating the properties that its members must satisfy...
as {C ∈ A : P(C)}. Thus the essence of the axiom is:
- Every subclass of a set that is defined by a predicate is itself a set.
The axiom schema of specification is characteristic of systems of axiomatic set theory related to the usual set theory ZFC, but does not usually appear in radically different systems of alternative set theory
Alternative set theory
Generically, an alternative set theory is an alternative mathematical approach to the concept of set. It is a proposed alternative to the standard set theory.Some of the alternative set theories are:*the theory of semisets...
. For example, New Foundations
New Foundations
In mathematical logic, New Foundations is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name...
and positive set theory use different restrictions of the axiom of comprehension of naive set theory
Naive set theory
Naive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...
. The Alternative Set Theory
Alternative set theory
Generically, an alternative set theory is an alternative mathematical approach to the concept of set. It is a proposed alternative to the standard set theory.Some of the alternative set theories are:*the theory of semisets...
of Vopenka makes a specific point of allowing proper subclasses of sets, called semiset
Semiset
In set theory, a semiset is a proper class which is contained in a set.The theory of semisets was proposed and developed by Czech mathematicians Petr Vopěnka and Petr Hájek . It is based on a modification of the von Neumann-Bernays-Gödel set theory; in standard NBG, the existence of semisets is...
s. Even in systems related to ZFC, this scheme is sometimes restricted to formulas with bounded quantifiers, as in Kripke–Platek set theory with urelements
Kripke–Platek set theory with urelements
The Kripke–Platek set theory with urelements is an axiom system for set theory with urelements that is considerably weaker than the familiar system ZF.-Preliminaries:...
.
Relation to the axiom schema of replacement
The axiom schema of separation can almost be derived from the axiom schema of replacementAxiom schema of replacement
In set theory, the axiom schema of replacement is a schema of axioms in Zermelo–Fraenkel set theory that asserts that the image of any set under any definable mapping is also a set...
.
First, recall this axiom schema:

for any functional predicate
Functional predicate
In formal logic and related branches of mathematics, a functional predicate, or function symbol, is a logical symbol that may be applied to an object term to produce another object term....
F in one variable
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
that doesn't use the symbols A, B, C or D.
Given a suitable predicate P for the axiom of specification, define the mapping F by F(D) = D if P(D) is true and F(D) = E if P(D) is false, where E is any member of A such that P(E) is true.
Then the set B guaranteed by the axiom of replacement is precisely the set B required for the axiom of specification. The only problem is if no such E exists. But in this case, the set B required for the axiom of separation is the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, so the axiom of separation follows from the axiom of replacement together with the axiom of empty set
Axiom of empty set
In axiomatic set theory, the axiom of empty set is an axiom of Zermelo–Fraenkel set theory, the fragment thereof Burgess calls ST, and Kripke–Platek set theory.- Formal statement :...
.
For this reason, the axiom schema of separation is often left out of modern lists of the Zermelo-Fraenkel axioms. However, it's still important for historical considerations, and for comparison with alternative axiomatizations of set theory, as can be seen for example in the following sections.
Unrestricted comprehension
The axiom schema of comprehension (unrestricted) reads: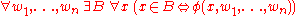
that is:
- There exists a set B whose members are precisely those objects that satisfy the predicate φ.
This set B is again unique, and is usually denoted as {x : φ(x, w_1, ... w_n)}.
This axiom schema was tacitly used in the early days of naive set theory
Naive set theory
Naive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...
, before a strict axiomatization was adopted. Unfortunately, it leads directly to Russell's paradox
Russell's paradox
In the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...
by taking φ(x) to be ¬(x∈x) (i.e., the property that set x is not a member of itself). Therefore, no useful axiomatization of set theory can use unrestricted comprehension, at least not with classical logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
.
Accepting only the axiom schema of specification was the beginning of axiomatic set theory. Most of the other Zermelo-Fraenkel axioms (but not the axiom of extensionality
Axiom of extensionality
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
or the axiom of regularity
Axiom of regularity
In mathematics, the axiom of regularity is one of the axioms of Zermelo-Fraenkel set theory and was introduced by...
) then became necessary to make up for some of what was lost by changing the axiom schema of comprehension to the axiom schema of specification – each of these axioms states that a certain set exists, and defines that set by giving a predicate for its members to satisfy, i.e. it is a special case of the axiom schema of comprehension.
In NBG class theory
In von Neumann-Bernays-Gödel set theory, a distinction is made between sets and classesClass (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
.
A class C is a set if and only if it belongs to some class E.
In this theory, there is a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
schema that reads:

that is:
- There is a class D such that any class C is a member of D if and only if C is a set that satisfies P.
This theorem schema is itself a restricted form of comprehension, which avoids Russell's paradox because of the requirement that C be a set.
Then specification for sets themselves can be written as a single axiom:
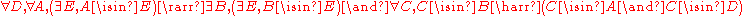
that is:
- Given any class D and any set A, there is a set B whose members are precisely those classes that are members of both A and D;
or even more simply:
- The intersectionIntersection (set theory)In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of a class D and a set A is itself a set B.
In this axiom, the predicate P is replaced by the class D, which can be quantified over.
In higher-order settings
In a typedType theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
language where we can quantify over predicates, the axiom schema of specification becomes a simple axiom. This is much the same trick as was used in the NBG axioms of the previous section, where the predicate was replaced by a class that was then quantified over.
In second-order logic
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
and higher-order logic
Higher-order logic
In mathematics and logic, a higher-order logic is a form of predicate logic that is distinguished from first-order logic by additional quantifiers and a stronger semantics...
with higher-order semantics, the axiom of specification is a logical validity and does not need to be explicitly included in a theory.
In Quine's New Foundations
In the New FoundationsNew Foundations
In mathematical logic, New Foundations is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name...
approach to set theory pioneered by W.V.O. Quine, the axiom of comprehension for a given predicate takes the unrestricted form, but the predicates that may be used in the schema are themselves restricted.
The predicate (C is not in C) is forbidden, because the same symbol C appears on both sides of the membership symbol (and so at different "relative types"); thus, Russell's paradox is avoided.
However, by taking P(C) to be (C = C), which is allowed, we can form a set of all sets. For details, see stratification
Stratification (mathematics)
-In mathematical logic:In mathematical logic, stratification is any consistent assignment of numbers to predicate symbols guaranteeing that a unique formal interpretation of a logical theory exists...
.

