Positive set theory
Encyclopedia
In mathematical logic
, positive set theory is the name for a class of alternative set theories
in which the axiom of comprehension
holds for at least the positive formulas
(the smallest class of formulas containing atomic membership and equality formulas and closed under conjunction, disjunction, existential and universal quantification).
Typically, the motivation for these theories is topological: the sets are the classes which are closed under a certain topology
. The closure conditions for the various constructions allowed in building positive formulas are readily motivated (and one can further justify the use of universal quantifiers bounded in sets to get generalized positive comprehension): the justification of the existential quantifier seems to require that the topology be compact.
The set theory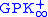
of Olivier Esser consists of the following axioms:
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, positive set theory is the name for a class of alternative set theories
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
in which the axiom of comprehension
- "
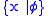exists"
holds for at least the positive formulas
(the smallest class of formulas containing atomic membership and equality formulas and closed under conjunction, disjunction, existential and universal quantification).Typically, the motivation for these theories is topological: the sets are the classes which are closed under a certain topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. The closure conditions for the various constructions allowed in building positive formulas are readily motivated (and one can further justify the use of universal quantifiers bounded in sets to get generalized positive comprehension): the justification of the existential quantifier seems to require that the topology be compact.
The set theory
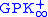of Olivier Esser consists of the following axioms:- The axiom of extensionalityAxiom of extensionalityIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
:
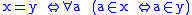. - The axiom of empty setAxiom of empty setIn axiomatic set theory, the axiom of empty set is an axiom of Zermelo–Fraenkel set theory, the fragment thereof Burgess calls ST, and Kripke–Platek set theory.- Formal statement :...
: there exists a set
such that 
(this axiom can be neatly dispensed with if a false formula 
is included as a positive formula). - The axiom of generalized positive comprehension: if
is a formula in predicate logic using only 
, 
, 
, 
, 
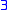, and 
, then the set of all 
such that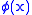 
is also a set. Quantification (
, 
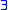) may be bounded.
- Note that negation is specifically not permitted.
- The axiom of closure: for every formula
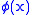, a set exists which is the intersection of all sets which contain every x such that 
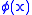; this is called the closure of 
and is written in any of the various ways that topological closures can be presented. This can be put more briefly if class language is allowed (any condition on sets defining a class as in NBGVon Neumann–Bernays–Gödel set theoryIn the foundations of mathematics, von Neumann–Bernays–Gödel set theory is an axiomatic set theory that is a conservative extension of the canonical axiomatic set theory ZFC. A statement in the language of ZFC is provable in NBG if and only if it is provable in ZFC. The ontology of NBG includes...
): for any class C there is a set which is the intersection of all sets which contain C as a subclass. This is obviously a reasonable principle if the sets are understood as closed classes in a topology. - The axiom of infinityAxiom of infinityIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of infinity is one of the axioms of Zermelo-Fraenkel set theory...
: the von Neumann ordinalOrdinal numberIn set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
exists. This is not an axiom of infinity in the usual sense; if Infinity does not hold, the closure of 
exists and has itself as its sole additional member (it is certainly infinite); the point of this axiom is that 
contains no additional elements at all, which boosts the theory from the strength of second order arithmetic to the strength of Morse–Kelley set theoryMorse–Kelley set theoryIn the foundation of mathematics, Morse–Kelley set theory or Kelley–Morse set theory is a first order axiomatic set theory that is closely related to von Neumann–Bernays–Gödel set theory...
with the proper class ordinal a weakly compact cardinalWeakly compact cardinalIn mathematics, a weakly compact cardinal is a certain kind of cardinal number introduced by ; weakly compact cardinals are large cardinals, meaning that their existence can not be proven from the standard axioms of set theory....
.
Interesting properties
- The universal setUniversal setIn set theory, a universal set is a set which contains all objects, including itself. In set theory as usually formulated, the conception of a set of all sets leads to a paradox...
is a proper set in this theory. - The sets of this theory are the collections of sets which are closed under a certain topologyTopologyTopology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
on the classes. - The theory can interpret ZFC (by restricting oneself to the class of well-founded sets, which is not itself a set). It in fact interprets a stronger theory (Morse-Kelley set theory with the proper class ordinal a weakly compact cardinalWeakly compact cardinalIn mathematics, a weakly compact cardinal is a certain kind of cardinal number introduced by ; weakly compact cardinals are large cardinals, meaning that their existence can not be proven from the standard axioms of set theory....
).
Researchers
- Isaac MalitzIsaac MalitzIsaac Richard Jay Malitz is a logician who introduced the subject of positive set theory in his 1976 Ph.D. Thesis at UCLA.- References :* – entry in the Mathematics Genealogy Project...
originally introduced Positive Set Theory in his 1976 PhD Thesis at UCLA - Alonzo ChurchAlonzo ChurchAlonzo Church was an American mathematician and logician who made major contributions to mathematical logic and the foundations of theoretical computer science. He is best known for the lambda calculus, Church–Turing thesis, Frege–Church ontology, and the Church–Rosser theorem.-Life:Alonzo Church...
was the chairman of the committee supervising the aforementioned thesis - Olivier Esser seems to be the most active in this field.