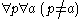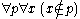Kripke–Platek set theory with urelements
Encyclopedia
The Kripke–Platek set theory with urelements (KPU) is an axiom system for set theory
with urelements that is considerably weaker than the familiar system ZF
.
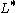 with a single binary relation symbol
with a single binary relation symbol 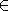 .
.
Letters of the sort designate urelements, of which there may be none, whereas letters of the sort
designate urelements, of which there may be none, whereas letters of the sort 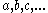 designate sets. The letters
designate sets. The letters 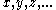 may denote both sets and urelements.
may denote both sets and urelements.
The letters for sets may appear on both sides of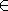 , while those for urelements may only appear on the left, i.e. the following are examples of valid expressions:
, while those for urelements may only appear on the left, i.e. the following are examples of valid expressions: 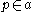 ,
, 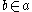 .
.
The statement of the axioms also requires reference to a certain collection of formulae called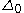 -formulae. The collection
-formulae. The collection 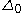 consists of those formulae that can be built using the constants,
consists of those formulae that can be built using the constants,  ,
,  ,
,  ,
,  , and bounded quantification. That is quantification of the form
, and bounded quantification. That is quantification of the form 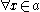 or
or 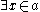 where
where  is given set.
is given set.
of KPU considered as sets inside a maximal universe that are transitive
as such are called admissible set
s.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
with urelements that is considerably weaker than the familiar system ZF
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
.
Preliminaries
The usual way of stating the axioms presumes a two sorted first order language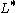 with a single binary relation symbol
with a single binary relation symbol 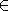 .
.Letters of the sort
 designate urelements, of which there may be none, whereas letters of the sort
designate urelements, of which there may be none, whereas letters of the sort 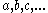 designate sets. The letters
designate sets. The letters 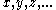 may denote both sets and urelements.
may denote both sets and urelements.The letters for sets may appear on both sides of
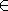 , while those for urelements may only appear on the left, i.e. the following are examples of valid expressions:
, while those for urelements may only appear on the left, i.e. the following are examples of valid expressions: 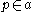 ,
, 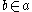 .
.The statement of the axioms also requires reference to a certain collection of formulae called
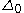 -formulae. The collection
-formulae. The collection 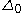 consists of those formulae that can be built using the constants,
consists of those formulae that can be built using the constants, 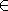 ,
,  ,
,  ,
,  , and bounded quantification. That is quantification of the form
, and bounded quantification. That is quantification of the form 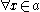 or
or 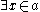 where
where  is given set.
is given set.Axioms
The axioms of KPU are the universal closures of the following formulae:- ExtensionalityAxiom of extensionalityIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
: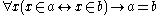
- FoundationAxiom of regularityIn mathematics, the axiom of regularity is one of the axioms of Zermelo-Fraenkel set theory and was introduced by...
: This is an axiom schemaAxiom schemaIn mathematical logic, an axiom schema generalizes the notion of axiom.An axiom schema is a formula in the language of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which...
where for every formula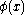 we have
we have 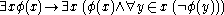 .
.
- PairingAxiom of pairingIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of pairing is one of the axioms of Zermelo–Fraenkel set theory.- Formal statement :...
: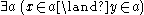
- UnionAxiom of unionIn axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of union is one of the axioms of Zermelo-Fraenkel set theory, stating that, for any set x there is a set y whose elements are precisely the elements of the elements of x...
: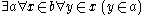
- Δ0-SeparationAxiom schema of predicative separationIn axiomatic set theory, the axiom schema of predicative separation, or of restricted, or Δ0 separation, is a schema of axioms which is a restriction of the usual axiom schema of separation in Zermelo-Fraenkel set theory. It only asserts the existence of a subset of a set if that subset can...
: This is again an axiom schemaAxiom schemaIn mathematical logic, an axiom schema generalizes the notion of axiom.An axiom schema is a formula in the language of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which...
, where for every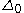 -formula
-formula 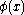 we have the following
we have the following 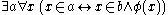 .
.
-
 -CollectionAxiom schema of replacementIn set theory, the axiom schema of replacement is a schema of axioms in Zermelo–Fraenkel set theory that asserts that the image of any set under any definable mapping is also a set...
-CollectionAxiom schema of replacementIn set theory, the axiom schema of replacement is a schema of axioms in Zermelo–Fraenkel set theory that asserts that the image of any set under any definable mapping is also a set...
: This is also an axiom schemaAxiom schemaIn mathematical logic, an axiom schema generalizes the notion of axiom.An axiom schema is a formula in the language of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which...
, for every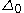 -formula
-formula 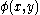 we have
we have  .
.
- Set Existence:
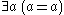
Additional assumptions
Technically these are axioms that describe the partition of objects into sets and urelements.Applications
KPU can be applied to the model theory of infinitary languages. ModelsModel theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
of KPU considered as sets inside a maximal universe that are transitive
Transitive set
In set theory, a set A is transitive, if* whenever x ∈ A, and y ∈ x, then y ∈ A, or, equivalently,* whenever x ∈ A, and x is not an urelement, then x is a subset of A....
as such are called admissible set
Admissible set
In set theory, a discipline within mathematics, an admissible set is a transitive set A\, such that \langle A,\in \rangle is a model of Kripke–Platek set theory....
s.
See also
- Axiomatic set theory
- Admissible setAdmissible setIn set theory, a discipline within mathematics, an admissible set is a transitive set A\, such that \langle A,\in \rangle is a model of Kripke–Platek set theory....
- Admissible ordinalAdmissible ordinalIn set theory, an ordinal number α is an admissible ordinal if Lα is an admissible set ; in other words, α is admissible when α is a limit ordinal and Lα⊧Σ0-collection....
- Kripke–Platek set theoryKripke–Platek set theoryThe Kripke–Platek axioms of set theory are a system of axioms for axiomatic set theory developed by Saul Kripke and Richard Platek. The axiom system, written in first-order logic, has an infinite number of axioms because an infinite axiom schema is used.KP is weaker than Zermelo–Fraenkel set theory...