Admissible set
Encyclopedia
In set theory
, a discipline within mathematics, an admissible set is a transitive set
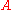such that 
is a model
of Kripke–Platek set theory
.
The smallest example of an admissible set is the set of hereditarily finite set
s. Another example is the set of hereditarily countable set
s.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a discipline within mathematics, an admissible set is a transitive set
Transitive set
In set theory, a set A is transitive, if* whenever x ∈ A, and y ∈ x, then y ∈ A, or, equivalently,* whenever x ∈ A, and x is not an urelement, then x is a subset of A....
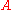such that is a modelModel theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
of Kripke–Platek set theory
Kripke–Platek set theory
The Kripke–Platek axioms of set theory are a system of axioms for axiomatic set theory developed by Saul Kripke and Richard Platek. The axiom system, written in first-order logic, has an infinite number of axioms because an infinite axiom schema is used.KP is weaker than Zermelo–Fraenkel set theory...
.
The smallest example of an admissible set is the set of hereditarily finite set
Hereditarily finite set
In mathematics and set theory, hereditarily finite sets are defined recursively as finite sets consisting of 0 or more hereditarily finite sets.-Formal definition:...
s. Another example is the set of hereditarily countable set
Hereditarily countable set
In set theory, a set is called hereditarily countable if it is a countable set of hereditarily countable sets. This inductive definition is in fact well-founded and can be expressed in the language of first-order set theory. A set is hereditarily countable if and only if it is countable, and every...
s.