
Poincaré conjecture
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Poincaré conjecture (pwɛ̃kaʁe, pwɛn.kɑˈreɪ ) is a theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
about the characterization
Characterization (mathematics)
In mathematics, the statement that "Property P characterizes object X" means, not simply that X has property P, but that X is the only thing that has property P. It is also common to find statements such as "Property Q characterises Y up to isomorphism". The first type of statement says in...
of the three-dimensional sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
(3-sphere), which is the hypersphere that bounds the unit ball in four-dimensional space. The conjecture states:
An equivalent form of the conjecture involves a coarser form of equivalence than homeomorphism called homotopy equivalence: if a 3-manifold is homotopy equivalent to the 3-sphere, then it is necessarily homeomorphic to it.
Originally conjectured by Henri Poincaré
Henri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
, the theorem concerns a space that locally looks like ordinary three-dimensional space but is connected, finite in size, and lacks any boundary (a closed
Closed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
). The Poincaré conjecture claims that if such a space has the additional property that each loop
Path (topology)
In mathematics, a path in a topological space X is a continuous map f from the unit interval I = [0,1] to XThe initial point of the path is f and the terminal point is f. One often speaks of a "path from x to y" where x and y are the initial and terminal points of the path...
in the space can be continuously tightened to a point, then it is necessarily a three-dimensional sphere. An analogous result
Generalized Poincaré conjecture
In the mathematical area of topology, the term Generalized Poincaré conjecture refers to a statement that a manifold which is a homotopy sphere 'is' a sphere. More precisely, one fixes a...
has been known in higher dimensions for some time.
After nearly a century of effort by mathematicians, Grigori Perelman
Grigori Perelman
Grigori Yakovlevich Perelman is a Russian mathematician who has made landmark contributions to Riemannian geometry and geometric topology.In 1992, Perelman proved the soul conjecture. In 2002, he proved Thurston's geometrization conjecture...
presented a proof of the conjecture in three papers made available in 2002 and 2003 on arXiv
ArXiv
The arXiv |Chi]], χ) is an archive for electronic preprints of scientific papers in the fields of mathematics, physics, astronomy, computer science, quantitative biology, statistics, and quantitative finance which can be accessed online. In many fields of mathematics and physics, almost all...
. The proof followed on from the program of Richard Hamilton
Richard Hamilton (professor)
Richard Streit Hamilton is Davies Professor of mathematics at Columbia University.He received his B.A in 1963 from Yale University and Ph.D. in 1966 from Princeton University. Robert Gunning supervised his thesis...
to use the Ricci flow to attack the problem. Perelman introduced a modification of the standard Ricci flow, called Ricci flow with surgery to systematically excise singular regions as they develop, in a controlled way. Several high-profile teams of mathematicians have verified that Perelman's proof is correct.
The Poincaré conjecture, before being proven, was one of the most important open questions in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. It is one of the seven Millennium Prize Problems
Millennium Prize Problems
The Millennium Prize Problems are seven problems in mathematics that were stated by the Clay Mathematics Institute in 2000. As of September 2011, six of the problems remain unsolved. A correct solution to any of the problems results in a US$1,000,000 prize being awarded by the institute...
, for which the Clay Mathematics Institute
Clay Mathematics Institute
The Clay Mathematics Institute is a private, non-profit foundation, based in Cambridge, Massachusetts. The Institute is dedicated to increasing and disseminating mathematical knowledge. It gives out various awards and sponsorships to promising mathematicians. The institute was founded in 1998...
offered a $1,000,000 prize for the first correct solution. Perelman's work survived review and was confirmed in 2006, leading to his being offered a Fields Medal
Fields Medal
The Fields Medal, officially known as International Medal for Outstanding Discoveries in Mathematics, is a prize awarded to two, three, or four mathematicians not over 40 years of age at each International Congress of the International Mathematical Union , a meeting that takes place every four...
, which he declined. Perelman was awarded the Millennium Prize on March 18, 2010. On July 1, 2010, he turned down the prize saying that he believes his contribution in proving the Poincaré conjecture was no greater than that of Hamilton's (who first suggested using the Ricci flow for the solution). The Poincaré conjecture is the first and, as of November 2011, the only solved Millennium problem.
On December 22, 2006, the journal Science
Science (journal)
Science is the academic journal of the American Association for the Advancement of Science and is one of the world's top scientific journals....
honored Perelman's proof of the Poincaré conjecture as the scientific "Breakthrough of the Year
Breakthrough of the Year
The Breakthrough of the Year is an annual award made by the journal Science for the most significant development in scientific research. Originating in 1989 as the Molecule of the Year, inspired by Time's Man of the Year, it was renamed the Breakthrough of the Year in 1996...
", the first time this had been bestowed in the area of mathematics.
Poincaré's question
At the beginning of the 20th century, Henri PoincaréHenri Poincaré
Jules Henri Poincaré was a French mathematician, theoretical physicist, engineer, and a philosopher of science...
was working on the foundations of topology—what would later be called combinatorial topology
Combinatorial topology
In mathematics, combinatorial topology was an older name for algebraic topology, dating from the time when topological invariants of spaces were regarded as derived from combinatorial decompositions such as simplicial complexes...
and then algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
. He was particularly interested in what topological properties characterized a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
.
Poincaré claimed in 1900 that homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
, a tool he had devised based on prior work by Enrico Betti
Enrico Betti
-External links:...
, was sufficient to tell if a 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
was a 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
. However, in a 1904 paper he described a counterexample to this claim, a space now called the Poincaré homology sphere. The Poincaré sphere was the first example of a homology sphere
Homology sphere
In algebraic topology, a homology sphere is an n-manifold X having the homology groups of an n-sphere, for some integer n ≥ 1. That is,andTherefore X is a connected space, with one non-zero higher Betti number: bn...
, a manifold that had the same homology as a sphere, of which many others have since been constructed. To establish that the Poincaré sphere was different from the 3-sphere, Poincaré introduced a new topological invariant, the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
, and showed that the Poincaré sphere had a fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of order 120, while the 3-sphere had a trivial fundamental group. In this way he was able to conclude that these two spaces were, indeed, different.
In the same paper, Poincaré wondered whether a 3-manifold with the homology of a 3-sphere and also trivial fundamental group had to be a 3-sphere. Poincaré's new condition—i.e., "trivial fundamental group"—can be restated as "every loop can be shrunk to a point."
The original phrasing was as follows:
Poincaré never declared whether he believed this additional condition would characterize the 3-sphere, but nonetheless, the statement that it does is known as the Poincaré conjecture. Here is the standard form of the conjecture:
Attempted solutions
This problem seems to have lain dormant for a time, until J. H. C. WhiteheadJ. H. C. Whitehead
John Henry Constantine Whitehead FRS , known as Henry, was a British mathematician and was one of the founders of homotopy theory. He was born in Chennai , in India, and died in Princeton, New Jersey, in 1960....
revived interest in the conjecture, when in the 1930s he first claimed a proof, and then retracted it. In the process, he discovered some interesting examples of simply connected non-compact 3-manifolds not homeomorphic to R3, the prototype of which is now called the Whitehead manifold
Whitehead manifold
In mathematics, the Whitehead manifold is an open 3-manifold that is contractible, but not homeomorphic to R3. Henry Whitehead discovered this puzzling object while he was trying to prove the Poincaré conjecture....
.
In the 1950s and 1960s, other mathematicians were to claim proofs only to discover a flaw. Influential mathematicians such as Bing
RH Bing
R. H. Bing was an American mathematician who worked mainly in the areas of geometric topology and continuum theory...
, Haken
Wolfgang Haken
Wolfgang Haken is a mathematician who specializes in topology, in particular 3-manifolds.In 1976 together with colleague Kenneth Appel at the University of Illinois at Urbana-Champaign, Haken solved one of the most famous problems in mathematics, the four-color theorem...
, Moise
Edwin E. Moise
Edwin Evariste Moise was an American mathematician and mathematics education reformer. After his retirement from mathematics he became a literary critic of 19th century English poetry and had several notes published in that field.-Early life and education:...
, and Papakyriakopoulos
Christos Papakyriakopoulos
Christos Dimitriou Papakyriakopoulos, commonly known as "Papa" , was a Greek mathematician specializing in geometric topology. He worked in isolation at Athens University being awarded a Ph.D on the recommendation of Carathéodory...
attacked the conjecture. In 1958 Bing proved a weak version of the Poincaré conjecture: if every simple closed curve of a compact 3-manifold is contained in a 3-ball, then the manifold is homeomorphic to the 3-sphere. Bing also described some of the pitfalls in trying to prove the Poincaré conjecture.
Over time, the conjecture gained the reputation of being particularly tricky to tackle. John Milnor commented that sometimes the errors in false proofs can be "rather subtle and difficult to detect." Work on the conjecture improved understanding of 3-manifolds. Experts in the field were often reluctant to announce proofs, and tended to view any such announcement with skepticism. The 1980s and 1990s witnessed some well-publicized fallacious proofs (which were not actually published in peer-reviewed
Peer review
Peer review is a process of self-regulation by a profession or a process of evaluation involving qualified individuals within the relevant field. Peer review methods are employed to maintain standards, improve performance and provide credibility...
form).
An exposition of attempts to prove this conjecture can be found in the non-technical book Poincaré's Prize by George Szpiro.
Dimensions
The classification of closed surfaces gives an affirmative answer to the analogous question in two dimensions. For dimensions greater than three, one can pose the Generalized Poincaré conjecture: is a homotopy n-sphereHomotopy sphere
In algebraic topology, a branch of mathematics, a homotopy sphere is an n-manifold homotopy equivalent to the n-sphere. It thus has the same homotopy groups and the same homology groups, as the n-sphere...
homeomorphic to the n-sphere? A stronger assumption is necessary; in dimensions four and higher there are simply-connected manifolds which are not homeomorphic to an n-sphere.
Historically, while the conjecture in dimension three seemed plausible, the generalized conjecture was thought to be false. In 1961 Stephen Smale
Stephen Smale
Steven Smale a.k.a. Steve Smale, Stephen Smale is an American mathematician from Flint, Michigan. He was awarded the Fields Medal in 1966, and spent more than three decades on the mathematics faculty of the University of California, Berkeley .-Education and career:He entered the University of...
shocked mathematicians by proving the Generalized Poincaré conjecture for dimensions greater than four and extended his techniques to prove the fundamental h-cobordism theorem. In 1982 Michael Freedman
Michael Freedman
Michael Hartley Freedman is a mathematician at Microsoft Station Q, a research group at the University of California, Santa Barbara. In 1986, he was awarded a Fields Medal for his work on the Poincaré conjecture. Freedman and Robion Kirby showed that an exotic R4 manifold exists.Freedman was born...
proved the Poincaré conjecture in dimension four. Freedman's work left open the possibility that there is a smooth four-manifold homeomorphic to the four-sphere which is not diffeomorphic
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
to the four-sphere. This so-called smooth Poincaré conjecture, in dimension four, remains open and is thought to be very difficult. Milnor's exotic sphere
Exotic sphere
In differential topology, a mathematical discipline, an exotic sphere is a differentiable manifold M that is homeomorphic but not diffeomorphic to the standard Euclidean n-sphere...
s show that the smooth Poincaré conjecture is false in dimension seven, for example.
These earlier successes in higher dimensions left the case of three dimensions in limbo. The Poincaré conjecture was essentially true in both dimension four and all higher dimensions for substantially different reasons. In dimension three, the conjecture had an uncertain reputation until the geometrization conjecture
Geometrization conjecture
Thurston's geometrization conjecture states that compact 3-manifolds can be decomposed canonically into submanifolds that have geometric structures. The geometrization conjecture is an analogue for 3-manifolds of the uniformization theorem for surfaces...
put it into a framework governing all 3-manifolds. John Morgan
John Morgan (mathematician)
John Willard Morgan is an American mathematician, well known for his contributions to topology and geometry. He is currently the director of the Simons Center for Geometry and Physics at Stony Brook University.-Life:...
wrote:
Hamilton's program and Perelman's solution
Hamilton's program was started in his 1982 paper in which he introduced the Ricci flowRicci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
on a manifold and showed how to use it to prove some special cases of the Poincaré conjecture. In the following years he extended this work, but was unable to prove the conjecture. The actual solution was not found until Grigori Perelman
Grigori Perelman
Grigori Yakovlevich Perelman is a Russian mathematician who has made landmark contributions to Riemannian geometry and geometric topology.In 1992, Perelman proved the soul conjecture. In 2002, he proved Thurston's geometrization conjecture...
published his papers.
In late 2002 and 2003 Perelman posted three papers on the arXiv
ArXiv
The arXiv |Chi]], χ) is an archive for electronic preprints of scientific papers in the fields of mathematics, physics, astronomy, computer science, quantitative biology, statistics, and quantitative finance which can be accessed online. In many fields of mathematics and physics, almost all...
. In these papers he sketched a proof of the Poincaré conjecture and a more general conjecture, Thurston's geometrization conjecture, completing the Ricci flow program outlined earlier by Richard Hamilton.
From May to July 2006, several groups presented papers that filled in the details of Perelman's proof of the Poincaré conjecture, as follows:
- Bruce KleinerBruce KleinerBruce Alan Kleiner is an American mathematician, working in differential geometry and topology and geometric group theory.He received his Ph.D. in 1990 from the University of California, Berkeley. His advisor was Wu-Yi Hsiang. He is now Professor of Mathematics at New York University.Kleiner has...
and John W. LottJohn Lott (mathematician)John Lott is a Professor of Mathematics at the University of California, Berkeley. He is working on Ricci flow....
posted a paper on the arXiv in May 2006 which filled in the details of Perelman's proof of the geometrization conjecture. - Huai-Dong CaoHuai-Dong CaoHuai-Dong Cao is A. Everett Pitcher Professor of Mathematics at Lehigh University. He collaborated with Xi-Ping Zhu of Zhongshan University in verifying Grigori Perelman's proof of the Poincaré conjecture. The Cao–Zhu team is one of three teams formed for this purpose...
and Xi-Ping ZhuXi-Ping ZhuZhu Xiping is a Professor of Mathematics at Sun Yat-sen University. He collaborated with Cao Huaidong of Lehigh University in verifying Grigori Perelman's proof of the Poincaré conjecture. The Cao–Zhu team was one of three teams formed for this purpose...
published a paper in the June 2006 issue of the Asian Journal of MathematicsAsian Journal of MathematicsThe Asian Journal of Mathematics is a peer-reviewed scientific journal covering all areas of pure and theoretical applied mathematics. It is published by International Press....
with an exposition of the complete proof of the Poincaré and geometrization conjectures. They initially implied the proof was their own achievement based on the "Hamilton-Perelman theory", but later retracted the original version of their paper, and posted a revised version, in which they referred to their work as the more modest "exposition of Hamilton–Perelman's proof". They also published an erratumErratumAn erratum or corrigendum is a correction of a book. An erratum is most commonly issued shortly after its original text is published. Patches to security issues in a computer program are also sometimes called errata. As a general rule, publishers issue an erratum for a production error An erratum...
disclosing that they had forgotten to cite properly the previous work of Kleiner and Lott published in 2003. In the same issue, the AJM editorial board issued an apology for what it called "incautions" in the Cao–Zhu paper. - John MorganJohn Morgan (mathematician)John Willard Morgan is an American mathematician, well known for his contributions to topology and geometry. He is currently the director of the Simons Center for Geometry and Physics at Stony Brook University.-Life:...
and Gang TianGang TianTian Gang is a Chinese mathematician and an academician of the Chinese Academy of Sciences. He is known for his contributions to geometric analysis and quantum cohomology, among other fields...
posted a paper on the arXiv in July 2006 which gave a detailed proof of just the Poincaré Conjecture (which is somewhat easier than the full geometrization conjecture) and expanded this to a book.
All three groups found that the gaps in Perelman's papers were minor and could be filled in using his own techniques.
On August 22, 2006, the ICM
International Congress of Mathematicians
The International Congress of Mathematicians is the largest conference for the topic of mathematics. It meets once every four years, hosted by the International Mathematical Union ....
awarded Perelman the Fields Medal
Fields Medal
The Fields Medal, officially known as International Medal for Outstanding Discoveries in Mathematics, is a prize awarded to two, three, or four mathematicians not over 40 years of age at each International Congress of the International Mathematical Union , a meeting that takes place every four...
for his work on the conjecture, but Perelman refused the medal.
John Morgan spoke at the ICM on the Poincaré conjecture on August 24, 2006, declaring that "in 2003, Perelman solved the Poincaré Conjecture."
In December 2006, the journal Science
Science (journal)
Science is the academic journal of the American Association for the Advancement of Science and is one of the world's top scientific journals....
honored the proof of Poincaré conjecture as the Breakthrough of the Year
Breakthrough of the Year
The Breakthrough of the Year is an annual award made by the journal Science for the most significant development in scientific research. Originating in 1989 as the Molecule of the Year, inspired by Time's Man of the Year, it was renamed the Breakthrough of the Year in 1996...
and featured it on its cover.
Ricci flow with surgery
Hamilton's program for proving the Poincaré conjecture involves first putting a Riemannian metric on the unknown simply connected closed 3-manifold. The idea is to try to improve this metric; for example, if the metric can be improved enough so that it has constant curvature, then it must be the 3-sphere. The metric is improved using the Ricci flowRicci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
equations;
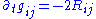
where g is the metric and R its Ricci curvature,
and one hopes that as the time t increases the manifold becomes easier to understand. Ricci flow expands the negative curvature part of the manifold and contracts the positive curvature part.
In some cases Hamilton was able to show that this works; for example, if the manifold has positive Ricci curvature everywhere he showed that the manifold becomes extinct in finite time under Ricci flow without any other singularities. (In other words, the manifold collapses to a point in finite time; it is easy to describe the structure just before the manifold collapses.) This easily implies the Poincaré conjecture in the case of positive Ricci curvature. However in general the Ricci flow equations lead to singularities of the metric after a finite time. Perelman showed how to continue past these singularities: very roughly, he cuts the manifold along the singularities, splitting the manifold into several pieces, and then continues with the Ricci flow on each of these pieces. This procedure is known as Ricci flow with surgery.
A special case of Perelman's theorems about Ricci flow with surgery is given as follows.
This result implies the Poincaré conjecture because it is easy to check it for the possible manifolds listed in the conclusion.
The condition on the fundamental group turns out to be necessary (and sufficient) for finite time extinction, and in particular includes the case of trivial fundamental group. It is equivalent to saying that the prime decomposition of the manifold has no acyclic components, and turns out to be equivalent to the condition that all geometric pieces of the manifold have geometries based on the two Thurston geometries S2×R and S3. By studying the limit of the manifold for large time, Perelman proved Thurston's geometrization conjecture for any fundamental group: at large times the manifold has a thick-thin decomposition, whose thick piece has a hyperbolic structure, and whose thin piece is a graph manifold
Graph manifold
In topology, a graph manifold is a 3-manifold which is obtained by gluing some circle bundles. They were invented and classified by the German topologist Friedhelm Waldhausen in 1967...
, but this extra complication is not necessary for proving just the Poincaré conjecture.
Solution
In November 2002, Grigori PerelmanGrigori Perelman
Grigori Yakovlevich Perelman is a Russian mathematician who has made landmark contributions to Riemannian geometry and geometric topology.In 1992, Perelman proved the soul conjecture. In 2002, he proved Thurston's geometrization conjecture...
posted the first of a series of eprints on arXiv
ArXiv
The arXiv |Chi]], χ) is an archive for electronic preprints of scientific papers in the fields of mathematics, physics, astronomy, computer science, quantitative biology, statistics, and quantitative finance which can be accessed online. In many fields of mathematics and physics, almost all...
outlining a solution of the Poincaré conjecture
Poincaré conjecture
In mathematics, the Poincaré conjecture is a theorem about the characterization of the three-dimensional sphere , which is the hypersphere that bounds the unit ball in four-dimensional space...
. Perelman's proof uses a modified version of a Ricci flow
Ricci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
program developed by Richard Hamilton. In August 2006, Perelman was awarded, but declined, the Fields Medal
Fields Medal
The Fields Medal, officially known as International Medal for Outstanding Discoveries in Mathematics, is a prize awarded to two, three, or four mathematicians not over 40 years of age at each International Congress of the International Mathematical Union , a meeting that takes place every four...
for his proof. On March 18, 2010, the Clay Mathematics Institute
Clay Mathematics Institute
The Clay Mathematics Institute is a private, non-profit foundation, based in Cambridge, Massachusetts. The Institute is dedicated to increasing and disseminating mathematical knowledge. It gives out various awards and sponsorships to promising mathematicians. The institute was founded in 1998...
awarded Perelman the $1 million Millennium Prize
Millennium Prize Problems
The Millennium Prize Problems are seven problems in mathematics that were stated by the Clay Mathematics Institute in 2000. As of September 2011, six of the problems remain unsolved. A correct solution to any of the problems results in a US$1,000,000 prize being awarded by the institute...
in recognition of his proof.
Perelman rejected that prize as well.
Perelman proved the conjecture by deforming the manifold using something called the Ricci flow (which behaves similarly to the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
that describes the diffusion of heat through an object). The Ricci flow usually deforms the manifold towards a rounder shape, except for some cases where it stretches the manifold apart from itself towards what are known as singularities
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
. Perelman and Hamilton then chop the manifold at the singularities (a process called "surgery") causing the separate pieces to form into ball-like shapes. Major steps in the proof involve showing how manifolds behave when they are deformed by the Ricci flow, examining what sort of singularities develop, determining whether this surgery process can be completed and establishing that the surgery need not be repeated infinitely many times.
The first step is to deform the manifold using the Ricci flow
Ricci flow
In differential geometry, the Ricci flow is an intrinsic geometric flow. It is a process that deforms the metric of a Riemannian manifold in a way formally analogous to the diffusion of heat, smoothing out irregularities in the metric....
. The Ricci flow was defined by Richard Hamilton as a way to deform manifolds. The formula for the Ricci flow is an imitation of the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
which describes the way heat flows in a solid. Like the heat flow, Ricci flow tends towards uniform behavior. Unlike the heat flow, the Ricci flow could run into singularities and stop functioning. A singularity in a manifold is a place where it is not differentiable: like a corner or a cusp or a pinching. The Ricci flow was only defined for smooth differentiable manifolds. Hamilton used the Ricci flow to prove that some compact manifolds were diffeomorphic to spheres and he hoped to apply it to prove the Poincaré Conjecture. He needed to understand the singularities.
Hamilton created a list of possible singularities that could form but he was concerned that some singularities might lead to difficulties. He wanted to cut the manifold at the singularities and paste in caps, and then run the Ricci flow again, so he needed to understand the singularities and show that certain kinds of singularities do not occur. Perelman discovered the singularities were all very simple: essentially three-dimensional cylinders made out of spheres stretched out along a line. An ordinary cylinder is made by taking circles stretched along a line. Perelman proved this using something called the "Reduced Volume" which is closely related to an eigenvalue of a certain elliptic equation.
Sometimes an otherwise complicated operation reduces to multiplication by a scalar
Scalar
Scalar may refer to:*Scalar , a quantity used to multiply vectors in the context of vector spaces*Scalar , a quantity which is independent of specific classes of coordinate systems...
(a number). Such numbers are called eigenvalues of that operation. Eigenvalues are closely related to vibration frequencies and are used in analyzing a famous problem: can you hear the shape of a drum?. Essentially an eigenvalue is like a note being played by the manifold. Perelman proved this note goes up as the manifold is deformed by the Ricci flow. This helped him eliminate some of the more troublesome singularities that had concerned Hamilton, particularly the cigar soliton solution, which looked like a strand sticking out of a manifold with nothing on the other side. In essence Perelman showed that all the strands that form can be cut and capped and none stick out on one side only.
Completing the proof, Perelman takes any compact, simply connected, three-dimensional manifold without boundary and starts to run the Ricci flow. This deforms the manifold into round pieces with strands running between them. He cuts the strands and continues deforming the manifold until eventually he is left with a collection of round three-dimensional spheres. Then he rebuilds the original manifold by connecting the spheres together with three-dimensional cylinders, morphs them into a round shape and sees that, despite all the initial confusion, the manifold was in fact homeomorphic to a sphere. This process is described in the fictional work by Tina S. Chang cited below.
One immediate question was how can one be sure there aren't infinitely many cuts necessary? Otherwise the cutting might progress forever. Perelman proved this can't happen by using minimal surfaces on the manifold. A minimal surface is essentially a soap film. Hamilton had shown that the area of
a minimal surface decreases as the manifold undergoes Ricci flow. Perelman verified what happened to the area of the minimal surface when the manifold was sliced. He proved that eventually the area is so small that any cut after the area is that small can only be chopping off three-dimensional spheres and not more complicated pieces. This is described as a battle with a Hydra by Sormani in Szpiro's book cited below. This last part of the proof appeared in Perelman's third and final paper on the subject.
External links
- The Poincaré conjecture described by the Clay Mathematics Institute.
- The Poincaré Conjecture (video) Brief visual overview of the Poincaré Conjecture, background and solution.
- The Geometry of 3-Manifolds(video) A public lecture on the Poincaré and geometrization conjectures, given by C. McMullen at Harvard in 2006.
- Bruce Kleiner (Yale) and John W. Lott (University of Michigan): "Notes & commentary on Perelman's Ricci flow papers".
- Stephen Ornes, What is The Poincaré Conjecture?, Seed Magazine, 25 August 2006.
- The slides used by Yau in a popular talk on the Poincaré conjecture.
- "The Poincaré Conjecture" – BBC Radio 4BBC Radio 4BBC Radio 4 is a British domestic radio station, operated and owned by the BBC, that broadcasts a wide variety of spoken-word programmes, including news, drama, comedy, science and history. It replaced the BBC Home Service in 1967. The station controller is currently Gwyneth Williams, and the...
programme In Our TimeIn Our Time (BBC Radio 4)In Our Time is a live BBC radio discussion series exploring the history of ideas, presented by Melvyn Bragg since 15 October 1998.. It is one of BBC radio's most successful discussion programmes, acknowledged to have "transformed the landscape for serious ideas at peak listening time"...
, 2 November 2006. Contributors June Barrow-Green, Lecturer in the History of Mathematics at the Open UniversityOpen UniversityThe Open University is a distance learning and research university founded by Royal Charter in the United Kingdom...
, Ian StewartIan Stewart (mathematician)Ian Nicholas Stewart FRS is a professor of mathematics at the University of Warwick, England, and a widely known popular-science and science-fiction writer. He is the first recipient of the , awarded jointly by the LMS and the IMA for his work on promoting mathematics.-Biography:Stewart was born...
, Professor of Mathematics at the University of WarwickUniversity of WarwickThe University of Warwick is a public research university located in Coventry, United Kingdom...
, Marcus du SautoyMarcus du SautoyMarcus Peter Francis du Sautoy OBE is the Simonyi Professor for the Public Understanding of Science and a Professor of Mathematics at the University of Oxford. Formerly a Fellow of All Souls College, and Wadham College, he is now a Fellow of New College...
, Professor of Mathematics at the University of OxfordUniversity of OxfordThe University of Oxford is a university located in Oxford, United Kingdom. It is the second-oldest surviving university in the world and the oldest in the English-speaking world. Although its exact date of foundation is unclear, there is evidence of teaching as far back as 1096...
, and presenter Melvyn BraggMelvyn BraggMelvyn Bragg, Baron Bragg FRSL FRTS FBA, FRS FRSA is an English broadcaster and author best known for his work with the BBC and for presenting the The South Bank Show...
. - "Solving an Old Math Problem Nets Award, Trouble" – NPR segment, December 26, 2006.
Articles
- Taming the fourth dimension, by B. Schechter, New ScientistNew ScientistNew Scientist is a weekly non-peer-reviewed English-language international science magazine, which since 1996 has also run a website, covering recent developments in science and technology for a general audience. Founded in 1956, it is published by Reed Business Information Ltd, a subsidiary of...
, 17 July 2004, Vol 183 No 2456 - "Major math problem is believed solved", Wall Street Journal, July 21, 2006 explains the current Millennium Prize situation.
- The Shapes of Space, by G. P. Collins, Scientific AmericanScientific AmericanScientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...
, 2004 July, pp. 94–103 - If it looks like a sphere..., by E. Klarreich, Science NewsScience NewsScience News is an American bi-weekly magazine devoted to short articles about new scientific and technical developments, typically gleaned from recent scientific and technical journals. Science News has been published since 1922 by Society for Science & the Public, a non-profit organization...
Online, June 14, 2003, Vol 163, No. 24, p 376. - Elusive Proof, Elusive Prover: A New Mathematical Mystery, by Dennis OverbyeDennis OverbyeDennis Overbye is a science writer specializing in physics and cosmology.-Biography:Overbye received his B.S. in physics from M.I.T.—where he was a member of the Alpha Mu chapter of Phi Kappa Sigma—in 1966. He started work towards a master's degree in astronomy from U.C.L.A...
, New York Times, Science, August 15, 2006. - Geometrization of Three Manifolds via the Ricci Flow, by Mike AndersonMichael Anderson (differential geometer)Michael Anderson is a Professor of Mathematics inState University of New York at Stony Brook. He is a differential geometer working on geometrization of 3-manifolds, general relativity, Einstein metrics and AdS/CFT correspondence et cetera.Anderson got his BA from UC Santa Barbara his MA from UC...
(SUNY Stony Brook), Notices of the AMS, Vol 51, Number 2, (written for mathematicians) - Perelman's proof of the Poincaré conjecture: a nonlinear PDE perspective by Terence TaoTerence TaoTerence Chi-Shen Tao FRS is an Australian mathematician working primarily on harmonic analysis, partial differential equations, combinatorics, analytic number theory and representation theory...
, unpublished arxiv.org preprint (written for mathematicians).
Fiction
- Perelman's Song, by Tina S. Chang, listed on Kasman's Mathematical Fiction website, to appeared Math HorizonsMath HorizonsMath Horizons is a magazine aimed at undergraduates interested in mathematics, published by the Mathematical Association of America. It publishes expository articles about "beautiful mathematics" as well as articles about the culture of mathematics covering mathematical people, institutions, humor,...
.http://pulse.yahoo.com/_LYTXAIQ3BIDXHCARFNHZUUTF4Q/blog/articles/45709?listPage=index
Lectures
- Structures of Three-Manifolds, for the scientifically inclined audience by Shing-Tung YauShing-Tung YauShing-Tung Yau is a Chinese American mathematician working in differential geometry. He was born in Shantou, Guangdong Province, China into a family of scholars from Jiaoling, Guangdong Province....
(Harvard), June 20, 2006. - The Work of Grigori Perelman, talk by John LottJohn Lott (mathematician)John Lott is a Professor of Mathematics at the University of California, Berkeley. He is working on Ricci flow....
(University of MichiganUniversity of MichiganThe University of Michigan is a public research university located in Ann Arbor, Michigan in the United States. It is the state's oldest university and the flagship campus of the University of Michigan...
) International Congress of MathematiciansInternational Congress of MathematiciansThe International Congress of Mathematicians is the largest conference for the topic of mathematics. It meets once every four years, hosted by the International Mathematical Union ....
2006 Presentation, for mathematicians in all areas, excellent graphics - Perelman and the Poincaré Conjecture, talk by Christina Sormani (CUNY Graduate CenterCUNY Graduate CenterThe Graduate Center of the City University of New York brings together graduate education, advanced research, and public programming to midtown Manhattan hosting 4,600 students, 33 doctoral programs, 7 master's programs, and 30 research centers and institutes...
and Lehman CollegeLehman CollegeLehman College is one of the constituent colleges of the City University of New York, USA. Founded in 1931 as the Bronx campus of Hunter College, the school became an independent college within the City University in 1968. The college is named after Herbert Lehman, a former New York governor,...
) presented at Williams CollegeWilliams CollegeWilliams College is a private liberal arts college located in Williamstown, Massachusetts, United States. It was established in 1793 with funds from the estate of Ephraim Williams. Originally a men's college, Williams became co-educational in 1970. Fraternities were also phased out during this...
, Wellesley College, Lehman CollegeLehman CollegeLehman College is one of the constituent colleges of the City University of New York, USA. Founded in 1931 as the Bronx campus of Hunter College, the school became an independent college within the City University in 1968. The college is named after Herbert Lehman, a former New York governor,...
and Tufts UniversityTufts UniversityTufts University is a private research university located in Medford/Somerville, near Boston, Massachusetts. It is organized into ten schools, including two undergraduate programs and eight graduate divisions, on four campuses in Massachusetts and on the eastern border of France...
. Transparencies are posted for public use (same as the graphics above) and a guide for math professors interested in giving a similar talk (recommends studying the resources posted here).
Websites
- Clay Mathematics Institute has a description of the Poincaré Conjecture as a Millennium Problem by John MilnorJohn MilnorJohn Willard Milnor is an American mathematician known for his work in differential topology, K-theory and dynamical systems. He won the Fields Medal in 1962, the Wolf Prize in 1989, and the Abel Prize in 2011. Milnor is a distinguished professor at Stony Brook University...
(SUNY Stony BrookStony Brook, New YorkStony Brook is a hamlet located in the Town of Brookhaven in Suffolk County, New York, which is on the North Shore of Long Island...
) as well as a press release about the proof. - Intro Perelman Website by Christina Sormani, (CUNY Graduate CenterCUNY Graduate CenterThe Graduate Center of the City University of New York brings together graduate education, advanced research, and public programming to midtown Manhattan hosting 4,600 students, 33 doctoral programs, 7 master's programs, and 30 research centers and institutes...
and Lehman CollegeLehman CollegeLehman College is one of the constituent colleges of the City University of New York, USA. Founded in 1931 as the Bronx campus of Hunter College, the school became an independent college within the City University in 1968. The college is named after Herbert Lehman, a former New York governor,...
) was used as a framework for this article and a resource for the initial set of links. - Who cares about Poincaré?, by Jordan EllenbergJordan EllenbergJordan S. Ellenberg is a mathematician working as a Professor of Mathematics at the University of Wisconsin–Madison. His research covers a wide variety of topics within arithmetic geometry. He received both the A.B. and Ph.D...
, Slate, August 18, 2006, is for the layman - A Bit of Cosmic Background, by Robert Kusner, UMass Math Dept Newsletter 2007.
- Lectures on Perelman's proof by T. Tao.

