
Poisson sampling
Encyclopedia
In the theory of finite population sampling, Poisson sampling is a sampling
process where each element of the population
that is sampled is subjected to an independent
Bernoulli trial
which determines whether the element becomes part of the sample during the drawing of a single sample.
Each element of the population may have a different probability of being included in the sample. The probability of being included in a sample during the drawing of a single sample is denoted as the first-order inclusion probability
of that element. If all first-order inclusion probabilities are equal, Poisson sampling becomes equivalent to Bernoulli sampling
, which can therefore be considered to be a special case of Poisson sampling.
of the ith element of the population is denoted by the symbol πi and the second-order inclusion probability that a pair consisting of the ith and jth element of the population that is sampled is included in a sample during the drawing of a single sample is denoted by πij.
The following relation is valid during Poisson sampling:
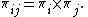
Sampling (statistics)
In statistics and survey methodology, sampling is concerned with the selection of a subset of individuals from within a population to estimate characteristics of the whole population....
process where each element of the population
Statistical population
A statistical population is a set of entities concerning which statistical inferences are to be drawn, often based on a random sample taken from the population. For example, if we were interested in generalizations about crows, then we would describe the set of crows that is of interest...
that is sampled is subjected to an independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
Bernoulli trial
Bernoulli trial
In the theory of probability and statistics, a Bernoulli trial is an experiment whose outcome is random and can be either of two possible outcomes, "success" and "failure"....
which determines whether the element becomes part of the sample during the drawing of a single sample.
Each element of the population may have a different probability of being included in the sample. The probability of being included in a sample during the drawing of a single sample is denoted as the first-order inclusion probability
Inclusion probability
In statistics, in the theory relating to sampling from finite populations, the inclusion probability of an element or member of the population is its probability of becoming part of the sample during the drawing of a single sample....
of that element. If all first-order inclusion probabilities are equal, Poisson sampling becomes equivalent to Bernoulli sampling
Bernoulli sampling
In the theory of finite population sampling, Bernoulli sampling is a sampling process where each element of the population that is sampled is subjected to an independent Bernoulli trial which determines whether the element becomes part of the sample during the drawing of a single sample...
, which can therefore be considered to be a special case of Poisson sampling.
A mathematical consequence of Poisson sampling
Mathematically, the first-order inclusion probabilityInclusion probability
In statistics, in the theory relating to sampling from finite populations, the inclusion probability of an element or member of the population is its probability of becoming part of the sample during the drawing of a single sample....
of the ith element of the population is denoted by the symbol πi and the second-order inclusion probability that a pair consisting of the ith and jth element of the population that is sampled is included in a sample during the drawing of a single sample is denoted by πij.
The following relation is valid during Poisson sampling:
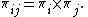
See also
- Bernoulli samplingBernoulli samplingIn the theory of finite population sampling, Bernoulli sampling is a sampling process where each element of the population that is sampled is subjected to an independent Bernoulli trial which determines whether the element becomes part of the sample during the drawing of a single sample...
- Poisson distributionPoisson distributionIn probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
- Poisson processPoisson processA Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
- Sampling designSampling designIn the theory of finite population sampling, a sampling design specifies for every possible sample its probability of being drawn.Mathematically, a sampling design is denoted by the function P which gives the probability of drawing a sample S....
Further reading
- Sarndal, Swenson, and Wretman (1992), Model Assisted Survey Sampling, Springer-Verlag, ISBN 0-387-40620-4

