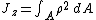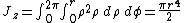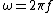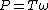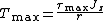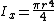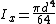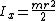Polar moment of inertia
Encyclopedia
Polar moment of inertia is a quantity used to predict an object's ability to resist torsion
, in objects (or segments of objects) with an invariant circular cross section
and no significant warping or out-of-plane deformation. It is used to calculate the angular displacement
of an object subjected to a torque
. It is analogous to the area moment of inertia, which characterizes an object's ability to resist bending
and is required to calculate displacement
.
The larger the polar moment of inertia, the less the beam will twist, when subjected to a given torque.
Polar moment of inertia should not be confused with moment of inertia
, which characterizes an object's angular acceleration
due to a torque
. See moment (physics)
.
can be substituted instead.
In objects with significant cross-sectional variation(along the axis of the applied torque), which cannot be analyzed in segments, a more complex approach may have to be used. See 3-D elasticity.
However the polar moment of inertia can be used to calculate the moment of inertia
of an object with arbitrary cross-section.
For a circular section with radius r:
unit for polar moment of inertia, like the area moment of inertia, is metre to the fourth power (m4).
, the following equation relates Jz to the area moments of inertia about the other two mutually perpendicular axes:
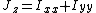
The polar moment of inertia appears in the formulae that describe torsional stress
and angular displacement.
Torsional stress:
where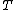 is the torque,
is the torque,  is the distance from the center and
is the distance from the center and 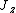 is the polar moment of inertia.
is the polar moment of inertia.
In a circular shaft, the shear stress
is maximal at the surface of the shaft (as that is where the torque is maximal):
Most frequently the inverse problem is solved, in which one solves for the radius.
 Calculation of the steam turbine
Calculation of the steam turbine
shaft radius for a turboset:
Assumptions:
The angular frequency
can be calculated with the following formula:
The torque carried by the shaft is related to the power
by the following equation:
The angular frequency is therefore 314.16 rad
/s
and the torque 3.1831 x 106 N·m
.
The maximal torque is:
After substitution of the polar moment of inertia the following expression is obtained:
The radius
is 0.200 m. If one adds a factor of safety
of 5 and re-calculates the radius with the maximal stress equal to the yield stress/5 the result is a radius of 0.343 m, or a diameter
of 69 cm, the approximate size of a turboset shaft in a nuclear power plant.
or
where:
or
Torsion (mechanics)
In solid mechanics, torsion is the twisting of an object due to an applied torque. In sections perpendicular to the torque axis, the resultant shear stress in this section is perpendicular to the radius....
, in objects (or segments of objects) with an invariant circular cross section
Cross section (geometry)
In geometry, a cross-section is the intersection of a figure in 2-dimensional space with a line, or of a body in 3-dimensional space with a plane, etc...
and no significant warping or out-of-plane deformation. It is used to calculate the angular displacement
Angular displacement
Angular displacement of a body is the angle in radians through which a point or line has been rotated in a specified sense about a specified axis....
of an object subjected to a torque
Torque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
. It is analogous to the area moment of inertia, which characterizes an object's ability to resist bending
Bending
In engineering mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element. The structural element is assumed to be such that at least one of its dimensions is a small fraction, typically...
and is required to calculate displacement
Displacement (vector)
A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
.
The larger the polar moment of inertia, the less the beam will twist, when subjected to a given torque.
Polar moment of inertia should not be confused with moment of inertia
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
, which characterizes an object's angular acceleration
Angular acceleration
Angular acceleration is the rate of change of angular velocity over time. In SI units, it is measured in radians per second squared , and is usually denoted by the Greek letter alpha .- Mathematical definition :...
due to a torque
Torque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
. See moment (physics)
Moment (physics)
In physics, the term moment can refer to many different concepts:*Moment of force is the tendency of a force to twist or rotate an object; see the article torque for details. This is an important, basic concept in engineering and physics. A moment is valued mathematically as the product of the...
.
Limitations
The polar moment of inertia cannot be used to analyze shafts with non-circular cross-sections. In such cases, the torsion constantTorsion constant
The torsion constant is a geometrical property of a beam's cross-section which is involved in the relationship between angle of twist and applied torque along the axis of the bar, for a homogeneous linear-elastic bar. That is, the torsion constant describes a beam's torsional stiffness.- History...
can be substituted instead.
In objects with significant cross-sectional variation(along the axis of the applied torque), which cannot be analyzed in segments, a more complex approach may have to be used. See 3-D elasticity.
However the polar moment of inertia can be used to calculate the moment of inertia
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
of an object with arbitrary cross-section.
Definition
- Jz = the polar moment of inertia about the axis z
- dA = an elemental area
- ρ = the radial distance to the element dA from the axis z
For a circular section with radius r:
Unit
The SISi
Si, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
unit for polar moment of inertia, like the area moment of inertia, is metre to the fourth power (m4).
Conversion from Area Moment of Inertia
By the perpendicular axis theoremPerpendicular axis theorem
In physics, the perpendicular axis theorem can be used to determine the moment of inertia of a rigid object that lies entirely within a plane, about an axis perpendicular to the plane, given the moments of inertia of the object about two perpendicular axes lying within the plane...
, the following equation relates Jz to the area moments of inertia about the other two mutually perpendicular axes:
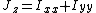
Application
NOTE: The following is only true for a circular or hollow circular section.The polar moment of inertia appears in the formulae that describe torsional stress
Shear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
and angular displacement.
Torsional stress:
where
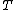 is the torque,
is the torque,  is the distance from the center and
is the distance from the center and 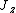 is the polar moment of inertia.
is the polar moment of inertia.In a circular shaft, the shear stress
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
is maximal at the surface of the shaft (as that is where the torque is maximal):
Most frequently the inverse problem is solved, in which one solves for the radius.
Sample calculation

Steam turbine
A steam turbine is a mechanical device that extracts thermal energy from pressurized steam, and converts it into rotary motion. Its modern manifestation was invented by Sir Charles Parsons in 1884....
shaft radius for a turboset:
Assumptions:
- Power carried by the shaft is 1000 MW; this is typical for a large nuclear powerNuclear powerNuclear power is the use of sustained nuclear fission to generate heat and electricity. Nuclear power plants provide about 6% of the world's energy and 13–14% of the world's electricity, with the U.S., France, and Japan together accounting for about 50% of nuclear generated electricity...
plant. - Yield stress of the steel used to make the shaft (τyield) is: 250 x 106 N/m².
- Electricity has a frequency of 50 HzHertzThe hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
; this is the typical frequency in Europe. In North America the frequency is 60 Hz.
The angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
can be calculated with the following formula:
The torque carried by the shaft is related to the power
Power (physics)
In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...
by the following equation:
The angular frequency is therefore 314.16 rad
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
/s
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
and the torque 3.1831 x 106 N·m
Newton metre
A newton metre is a unit of torque in the SI system. The symbolic form is N m or N·m, and sometimes hyphenated newton-metre...
.
The maximal torque is:
After substitution of the polar moment of inertia the following expression is obtained:
The radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
is 0.200 m. If one adds a factor of safety
Factor of safety
Factor of safety , also known as safety factor , is a term describing the structural capacity of a system beyond the expected loads or actual loads. Essentially, how much stronger the system is than it usually needs to be for an intended load...
of 5 and re-calculates the radius with the maximal stress equal to the yield stress/5 the result is a radius of 0.343 m, or a diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
of 69 cm, the approximate size of a turboset shaft in a nuclear power plant.
Polar moment of inertia
or
where:
- d is the diameterDiameterIn geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
- r is the radiusRadiusIn classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
Area moment of inertia
Moment of inertia
or
See also
- Torsion constantTorsion constantThe torsion constant is a geometrical property of a beam's cross-section which is involved in the relationship between angle of twist and applied torque along the axis of the bar, for a homogeneous linear-elastic bar. That is, the torsion constant describes a beam's torsional stiffness.- History...
- Torsion springTorsion springA torsion spring is a spring that works by torsion or twisting; that is, a flexible elastic object that stores mechanical energy when it is twisted. The amount of force it exerts is proportional to the amount it is twisted. There are two types...
- Torsion bar
- Area moment of inertia
External links
- Torsion of Shafts - engineeringtoolbox.com
- Elastic Properties and Young Modulus for some Materials - engineeringtoolbox.com