
Torsion constant
Encyclopedia
The torsion constant is a geometrical property of a beam's cross-section which is involved in the relationship between angle of twist and applied torque along the axis of the bar, for a homogeneous linear-elastic bar. That is, the torsion constant describes a beam's torsional stiffness
.
, which has an exact analytic equation, by assuming that a plane section before twisting remains plane after twisting, and a diameter remains a straight line.
Unfortunately, that assumption is correct only in beams with circular cross-sections, and is incorrect for any other shape.
For non-circular cross-sections, there are no exact analytical equations for finding the torsion constant. However approximate solutions have been found for many shapes.
Non-circular cross-section always have warping deformations that require numerical methods to allow the exact calculation of the torsion constant.
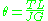
where is the angle of twist in radians
is the angle of twist in radians
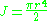
where
This is identical to the polar moment of inertia
and is exact.
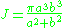
where
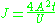
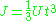
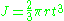
This is derived from the above equation for an arbitrary thin walled open tube of uniform thickness.
Stiffness
Stiffness is the resistance of an elastic body to deformation by an applied force along a given degree of freedom when a set of loading points and boundary conditions are prescribed on the elastic body.-Calculations:...
.
History
In 1820, the French engineer A. Duleau derived analytically that the torsion constant of a beam is identical to the polar moment of inertiaPolar moment of inertia
Polar moment of inertia is a quantity used to predict an object's ability to resist torsion, in objects with an invariant circular cross section and no significant warping or out-of-plane deformation. It is used to calculate the angular displacement of an object subjected to a torque...
, which has an exact analytic equation, by assuming that a plane section before twisting remains plane after twisting, and a diameter remains a straight line.
Unfortunately, that assumption is correct only in beams with circular cross-sections, and is incorrect for any other shape.
For non-circular cross-sections, there are no exact analytical equations for finding the torsion constant. However approximate solutions have been found for many shapes.
Non-circular cross-section always have warping deformations that require numerical methods to allow the exact calculation of the torsion constant.
Partial Derivation
For a beam of uniform cross-section along its length: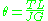
where
 is the angle of twist in radians
is the angle of twist in radians
- T is the applied torque
- L is the beam length
- J is the torsion constant (also referred to as torsional stiffness)
- G is the Modulus of rigidity (shear modulus) of the material
Circle
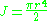
where
- r is the radius
This is identical to the polar moment of inertia
Polar moment of inertia
Polar moment of inertia is a quantity used to predict an object's ability to resist torsion, in objects with an invariant circular cross section and no significant warping or out-of-plane deformation. It is used to calculate the angular displacement of an object subjected to a torque...
and is exact.
Ellipse
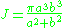
where
- a is the major radius
- b is the minor radius
Thin walled closed tube of uniform thickness
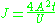
- A is the mean of the areas enclosed by the inner and outer boundaries
- t is the wall thickness
- U is the length of the median boundary
Thin walled open tube of uniform thickness
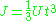
- t is the wall thickness
- U is the length of the median boundary
Circular thin walled open tube of uniform thickness
This is a tube with a slit cut longitudinally through its wall.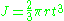
- t is the wall thickness
- r is the mean radius
This is derived from the above equation for an arbitrary thin walled open tube of uniform thickness.

