In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, in the field of combinatorics

Combinatorics

Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...

, a polar space of rank n (n ≥ 3), or projective index n−1, consists of a set P, conventionally the set of points, together with certain subsets of P, called subspaces, that satisfy these axioms :

• Every subspace, together with its own subspaces, is isomorphic with a projective geometry
  Projective space
  In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
  
   PG(d,q) with −1 ≤ d ≤ (n−1) and q a prime power. By definition, for each subspace the corresponding d is its dimension.
• The intersection of two subspaces is always a subspace.
• For each point p not in a subspace A of dimension of n−1, there is a unique subspace B of dimension n−1 such that A∩B is (n−2)-dimensional. The points in A∩B are exactly the points of A that are in a common subspace of dimension 1 with p.
• There are at least two disjoint subspaces of dimension n−1.

A polar space of rank two is a generalized quadrangle

Generalized quadrangle

A generalized quadrangle is an incidence structure. A generalized quadrangle is by definition a polar space of rank two. They are the generalized n-gons with n=4...

.

Examples

• In PG(d,q), with d odd and d ≥ 3, the set of all points, with as subspaces the totally isotropic subspaces of a random symplectic
  Symplectic topology
  Symplectic geometry is a branch of differential geometry and differential topology which studies symplectic manifolds; that is, differentiable manifolds equipped with a closed, nondegenerate 2-form...
  
   polarity, forms a polar space of rank (d+1)/2.
• Let Q be a nonsingular quadric
  Quadric
  In mathematics, a quadric, or quadric surface, is any D-dimensional hypersurface in -dimensional space defined as the locus of zeros of a quadratic polynomial...
  
   in PG(n,q) with character ω. Then the index of Q will be g = (n+w−3)/2. The set of all points on the quadric, together with the subspaces on the quadric, forms a polar space of rank g+1.
• Let H be a nonsingular Hermitian variety
  Hermitian variety
  Hermitian varieties are in a sense a generalisation of quadrics, and occur naturally in the theory of polarities.-Definition:Let K be a field with an involutive automorphism \theta...
  
   in PG(n,q²). The index of H will be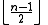 . The points on H, together with the subspaces on it, form a polar space of rank .

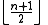Classification

Jacques Tits

Jacques Tits

Jacques Tits is a Belgian and French mathematician who works on group theory and geometry and who introduced Tits buildings, the Tits alternative, and the Tits group.- Career :Tits received his doctorate in mathematics at the age of 20...

proved that a finite polar space of rank at least three, is always isomorphic with one of the three structures given above. This leaves only the problem of classifying generalized quadrangles.