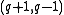Generalized quadrangle
Encyclopedia
A generalized quadrangle is an incidence structure
. A generalized quadrangle is by definition a polar space
of rank two. They are the generalized n-gon
s with . They are also precisely the partial geometries
. They are also precisely the partial geometries
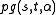 with
with 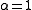 .
.
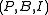 , with
, with 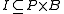 an incidence relation, satisfying certain axiom
an incidence relation, satisfying certain axiom
s. Elements of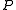 are by definition the points of the generalized quadrangle, elements of
are by definition the points of the generalized quadrangle, elements of 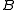 the lines. The axioms are the following:
the lines. The axioms are the following:
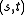 are the parameters of the generalized quadrangle.
are the parameters of the generalized quadrangle.
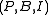 is a generalized quadrangle with parameters '
is a generalized quadrangle with parameters '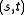 ', then
', then 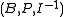 , with
, with  the inverse incidence relation, is also a generalized quadrangle. This is the dual generalized quadrangle. Its parameters are '
the inverse incidence relation, is also a generalized quadrangle. This is the dual generalized quadrangle. Its parameters are '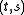 '. Even if
'. Even if 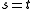 , the dual structure need not be isomorphic with the original structure.
, the dual structure need not be isomorphic with the original structure.
s of rank at least three, and extrapolating them to rank 2, one finds these (finite) generalized quadrangles :
 (this is just a grid)
(this is just a grid)
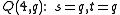
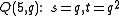
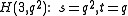
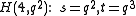
The generalized quadrangle derived from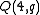 is always isomorphic with the dual of
is always isomorphic with the dual of 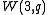 , and they are both self-dual and thus isomorphic to each other if and only if
, and they are both self-dual and thus isomorphic to each other if and only if  is even.
is even.
 ,
,  allows generalized quadrangles with parameters
allows generalized quadrangles with parameters 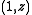 and
and 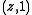 . Apart from that, only the following parameters have been found possible until now, with
. Apart from that, only the following parameters have been found possible until now, with 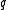 an arbitrary prime power
an arbitrary prime power
:
Incidence structure
In mathematics, an incidence structure is a tripleC=.\,where P is a set of "points", L is a set of "lines" and I \subseteq P \times L is the incidence relation. The elements of I are called flags. If \in I,...
. A generalized quadrangle is by definition a polar space
Polar space
In mathematics, in the field of combinatorics, a polar space of rank n , or projective index n−1, consists of a set P, conventionally the set of points, together with certain subsets of P, called subspaces, that satisfy these axioms :* Every subspace, together with its own subspaces, is isomorphic...
of rank two. They are the generalized n-gon
Generalized n-gon
In combinatorial theory, a generalized polygon is an incidence structure introduced by Jacques Tits. Generalized polygons encompass as special cases projective planes and generalized quadrangles , which form the most complex kinds of axiomatic projective and polar spaces...
s with
 . They are also precisely the partial geometries
. They are also precisely the partial geometriesPartial geometry
An incidence structure C= consists of points P, lines L, and flags I \subseteq P \times L where a point p is said to be incident with a line l if \in I...
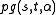 with
with 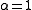 .
.Definition
A generalized quadrangle is an incidence structure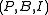 , with
, with 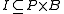 an incidence relation, satisfying certain axiom
an incidence relation, satisfying certain axiomAxiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s. Elements of
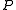 are by definition the points of the generalized quadrangle, elements of
are by definition the points of the generalized quadrangle, elements of 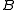 the lines. The axioms are the following:
the lines. The axioms are the following:
- There is a
 (
(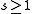 ) such that on every line there are exactly
) such that on every line there are exactly 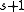 points. There is at most one point on two distinct lines.
points. There is at most one point on two distinct lines. - There is a
 (
( ) such that through every point there are exactly
) such that through every point there are exactly  lines. There is at most one line through two distinct points.
lines. There is at most one line through two distinct points. - For every point
 not on a line
not on a line  , there is a unique line
, there is a unique line  and a unique point
and a unique point  , such that
, such that 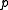 is on
is on 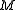 , and
, and 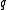 on
on 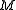 and
and 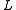 .
.
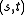 are the parameters of the generalized quadrangle.
are the parameters of the generalized quadrangle.Duality
If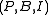 is a generalized quadrangle with parameters '
is a generalized quadrangle with parameters '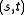 ', then
', then 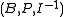 , with
, with  the inverse incidence relation, is also a generalized quadrangle. This is the dual generalized quadrangle. Its parameters are '
the inverse incidence relation, is also a generalized quadrangle. This is the dual generalized quadrangle. Its parameters are '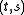 '. Even if
'. Even if 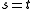 , the dual structure need not be isomorphic with the original structure.
, the dual structure need not be isomorphic with the original structure.Properties
-
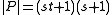
-

- When constructing a graph with as vertices the points of a generalized quadrangle, and with the collinear points connected, one finds a strongly regular graphStrongly regular graphIn graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
. -
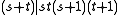
-
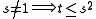
-
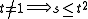
Classical generalized quadrangles
When looking at the different cases for polar spacePolar space
In mathematics, in the field of combinatorics, a polar space of rank n , or projective index n−1, consists of a set P, conventionally the set of points, together with certain subsets of P, called subspaces, that satisfy these axioms :* Every subspace, together with its own subspaces, is isomorphic...
s of rank at least three, and extrapolating them to rank 2, one finds these (finite) generalized quadrangles :
- A hyperbolic quadricQuadricIn mathematics, a quadric, or quadric surface, is any D-dimensional hypersurface in -dimensional space defined as the locus of zeros of a quadratic polynomial...
 , a parabolic quadric
, a parabolic quadric 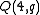 and an elliptic quadric
and an elliptic quadric  are the only possible quadrics in projective spaces over finite fields with projective index 1. We find these parameters respectively :
are the only possible quadrics in projective spaces over finite fields with projective index 1. We find these parameters respectively :
 (this is just a grid)
(this is just a grid)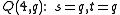
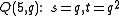
- A hermitian variety
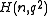 has projective index 1 if and only if n is 3 or 4. We find :
has projective index 1 if and only if n is 3 or 4. We find :
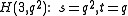
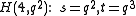
- A symplectic polarity in
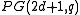 has a maximal isotropic subspace of dimension 1 if and only if
has a maximal isotropic subspace of dimension 1 if and only if  . Here, we find a generalized quadrangle
. Here, we find a generalized quadrangle 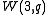 , with
, with  .
.
The generalized quadrangle derived from
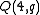 is always isomorphic with the dual of
is always isomorphic with the dual of 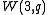 , and they are both self-dual and thus isomorphic to each other if and only if
, and they are both self-dual and thus isomorphic to each other if and only if  is even.
is even.Non-classical examples
- Let O be a hyperoval in
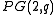 with q an even prime powerPrime powerIn mathematics, a prime power is a positive integer power of a prime number.For example: 5=51, 9=32 and 16=24 are prime powers, while6=2×3, 15=3×5 and 36=62=22×32 are not...
with q an even prime powerPrime powerIn mathematics, a prime power is a positive integer power of a prime number.For example: 5=51, 9=32 and 16=24 are prime powers, while6=2×3, 15=3×5 and 36=62=22×32 are not...
, and embed that projective (desarguesian) plane into
into 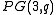 . Now consider the incidence structure
. Now consider the incidence structure 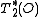 where the points are all points not in
where the points are all points not in  , the lines are those not on
, the lines are those not on  , intersecting
, intersecting  in a point of O, and the incidence is the natural one. This is a (q-1,q+1)-generalized quadrangle.
in a point of O, and the incidence is the natural one. This is a (q-1,q+1)-generalized quadrangle. - Let q be an integer (odd or even) and consider a symplectic polarity
 in
in  . Choose a random point p and define
. Choose a random point p and define  . Let the lines of our incidence structure be all absolute lines not on
. Let the lines of our incidence structure be all absolute lines not on  together with all lines through p which are not on
together with all lines through p which are not on  , and let the points be all points of
, and let the points be all points of 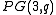 except those in
except those in  . The incidence is again the natural one. We obtain once again a (q-1,q+1)-generalized quadrangle
. The incidence is again the natural one. We obtain once again a (q-1,q+1)-generalized quadrangle
Restrictions on parameters
By using grids and dual grids, any integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
 ,
,  allows generalized quadrangles with parameters
allows generalized quadrangles with parameters 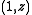 and
and 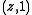 . Apart from that, only the following parameters have been found possible until now, with
. Apart from that, only the following parameters have been found possible until now, with 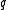 an arbitrary prime power
an arbitrary prime powerPrime power
In mathematics, a prime power is a positive integer power of a prime number.For example: 5=51, 9=32 and 16=24 are prime powers, while6=2×3, 15=3×5 and 36=62=22×32 are not...
:
-

-
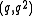 and
and 
-
 and
and 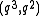
-
 and
and