Generalized n-gon
Encyclopedia
In combinatorial theory, a generalized polygon is an incidence structure introduced by Jacques Tits
. Generalized polygons encompass as special cases projective plane
s (generalized triangles, n = 3) and generalized quadrangle
s (n = 4), which form the most complex kinds of axiomatic projective
and polar
spaces. Many generalized polygons arise from groups of Lie type, but there are also exotic ones that cannot be obtained in this way. Generalized polygons satisfying a technical condition known as the Moufang
property have been completely classified by Tits and Weiss.
(P,L,I), where P is the set of points, L is the set of lines and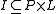
is the incidence relation, satisfying certain regularity conditions. In order to express them, consider the bipartite
incidence graph with the vertex set P ∪ L and the edges connecting the incident pairs of points and lines.
This condition is frequently stated as follows: any pair consisting of a point and a line is contained in an ordinary n-gon and there are no ordinary k-gons for k < n.
When it is important to specify the diameter, a generalized polygon of diameter n is called a generalized n-gon, and the normal names for small polygons are used.
A generalized polygon is of order (s,t) if:
We say a generalized polygon is thick if every point (line) is incident with at least three lines (points). All thick generalized polygons have an order.
The dual of a generalized n-gon (P,L,I) is the incidence structure (P,L,I-1), which is again a generalized n-gon.
and Graham Higman
proved that finite generalized n-gons with
s ≥ 2, t ≥ 2 can exist only for the following values of n:
Moreover,
If s and t are both infinite then generalized polygons exist for each n greater or equal to 2. It is unknown whether or not there exist generalized polygons with one of the parameters finite and the other infinite (these cases are called semi-finite).
Jacques Tits
Jacques Tits is a Belgian and French mathematician who works on group theory and geometry and who introduced Tits buildings, the Tits alternative, and the Tits group.- Career :Tits received his doctorate in mathematics at the age of 20...
. Generalized polygons encompass as special cases projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
s (generalized triangles, n = 3) and generalized quadrangle
Generalized quadrangle
A generalized quadrangle is an incidence structure. A generalized quadrangle is by definition a polar space of rank two. They are the generalized n-gons with n=4...
s (n = 4), which form the most complex kinds of axiomatic projective
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
and polar
Polar space
In mathematics, in the field of combinatorics, a polar space of rank n , or projective index n−1, consists of a set P, conventionally the set of points, together with certain subsets of P, called subspaces, that satisfy these axioms :* Every subspace, together with its own subspaces, is isomorphic...
spaces. Many generalized polygons arise from groups of Lie type, but there are also exotic ones that cannot be obtained in this way. Generalized polygons satisfying a technical condition known as the Moufang
Ruth Moufang
Ruth Moufang was a German mathematician.Born to a German chemist Dr. Eduard Moufang and Else Fecht Moufang, she studied mathematics at the University of Frankfurt. In 1931 she received her Ph.D. on projective geometry under the direction of Max Dehn, and in 1932 spent a fellowship year in Rome...
property have been completely classified by Tits and Weiss.
Definition
A generalized polygon is an incidence structureIncidence structure
In mathematics, an incidence structure is a tripleC=.\,where P is a set of "points", L is a set of "lines" and I \subseteq P \times L is the incidence relation. The elements of I are called flags. If \in I,...
(P,L,I), where P is the set of points, L is the set of lines and
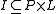is the incidence relation, satisfying certain regularity conditions. In order to express them, consider the bipartiteBipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
incidence graph with the vertex set P ∪ L and the edges connecting the incident pairs of points and lines.
- The girth of the incidence graph is twice the diameter of the incidence graph, which is usually denoted by n.
This condition is frequently stated as follows: any pair consisting of a point and a line is contained in an ordinary n-gon and there are no ordinary k-gons for k < n.
When it is important to specify the diameter, a generalized polygon of diameter n is called a generalized n-gon, and the normal names for small polygons are used.
A generalized polygon is of order (s,t) if:
- all vertices of the incidence graph corresponding to the elements of L have the same degree s + 1 for some natural number s; in other words, every line contains exactly s + 1 points,
- all vertices of the incidence graph corresponding to the elements of P have the same degree t + 1 for some natural number t; in other words, every point lies on exactly t + 1 lines.
We say a generalized polygon is thick if every point (line) is incident with at least three lines (points). All thick generalized polygons have an order.
The dual of a generalized n-gon (P,L,I) is the incidence structure (P,L,I-1), which is again a generalized n-gon.
Examples
- A generalized digon (n = 2) is a complete bipartite graphComplete bipartite graphIn the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
Ks+1,t+1.
- For any natural n ≥ 3, consider the boundary of the ordinary polygonPolygonIn geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
with n sides. Declare the vertices of the polygon to be the points and the sides to be the lines, with the usual incidence relation. This results in a generalized n-gon with s = t = 1.
- For each group of Lie typeGroup of Lie typeIn mathematics, a group of Lie type G is a group of rational points of a reductive linear algebraic group G with values in the field k. Finite groups of Lie type form the bulk of nonabelian finite simple groups...
G of rank 2 there is an associated generalized n-gon X with n equal to 3, 4, 6 or 8 such that G acts transitively on the set of flags of X. In the finite case, for n=6, one obtains the Split Cayley hexagon of order (q,q) for G2(q) and the twisted triality hexagon of order (q3,q) for 3D4(q3), and for n=8, one obtains the Ree-Tits octagon of order (q,q2) for 2F4(q) with q=22n+1. Up to duality, these are the only known thick finite generalized hexagons or octagons.
Feit-Higman theorem
Walter FeitWalter Feit
Walter Feit was a Jewish Austrian-American mathematician who worked in finite group theory and representation theory....
and Graham Higman
Graham Higman
Graham Higman FRS was a leading British mathematician. He is known for his contributions to group theory....
proved that finite generalized n-gons with
s ≥ 2, t ≥ 2 can exist only for the following values of n:
- 2, 3, 4, 6 or 8.
Moreover,
- If n = 2, the structure is a complete bipartite graph.
- If n = 3, the structure is a finite projective planeProjective planeIn mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
, and s = t. - If n = 4, the structure is a finite generalized quadrangleGeneralized quadrangleA generalized quadrangle is an incidence structure. A generalized quadrangle is by definition a polar space of rank two. They are the generalized n-gons with n=4...
, and t1/2 ≤ s ≤ t2. - If n = 6, then st is a squareSquare numberIn mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
, and t1/3 ≤ s ≤ t3. - If n = 8, then 2st is a square, and t1/2 ≤ s ≤ t2.
- If s or t is allowed to be 1 and the structure is not the ordinary n-gon then besides the values of n already listed, only n = 12 may be possible.
If s and t are both infinite then generalized polygons exist for each n greater or equal to 2. It is unknown whether or not there exist generalized polygons with one of the parameters finite and the other infinite (these cases are called semi-finite).