
Partial geometry
Encyclopedia
An incidence structure
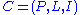 consists of points
consists of points 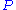 , lines
, lines 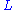 , and flags
, and flags  where a point
where a point  is said to be incident with a line
is said to be incident with a line  if
if 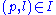 . It is a (finite) partial geometry if there are integer
. It is a (finite) partial geometry if there are integer
s such that:
such that:
A partial geometry with these parameters is denoted by .
.
Incidence structure
In mathematics, an incidence structure is a tripleC=.\,where P is a set of "points", L is a set of "lines" and I \subseteq P \times L is the incidence relation. The elements of I are called flags. If \in I,...
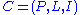 consists of points
consists of points 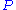 , lines
, lines 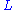 , and flags
, and flags  where a point
where a point  is said to be incident with a line
is said to be incident with a line  if
if 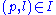 . It is a (finite) partial geometry if there are integer
. It is a (finite) partial geometry if there are integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s
 such that:
such that:- For any pair of distinct points
 and
and  , there is at most one line incident with both of them.
, there is at most one line incident with both of them. - Each line is incident with
 points.
points. - Each point is incident with
 lines.
lines. - If a point
 and a line
and a line  are not incident, there are exactly
are not incident, there are exactly  pairs
pairs 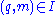 , such that
, such that 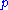 is incident with
is incident with  and
and 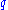 is incident with
is incident with 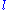 .
.
A partial geometry with these parameters is denoted by
 .
.Properties
- The number of points is given by
 and the number of lines by
and the number of lines by  .
. - The point graph of a
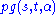 is a strongly regular graphStrongly regular graphIn graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
is a strongly regular graphStrongly regular graphIn graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
: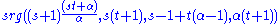 .
. - Partial geometries are dual structures : the dual of a
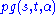 is simply a
is simply a  .
.
Special case
- The generalized quadrangleGeneralized quadrangleA generalized quadrangle is an incidence structure. A generalized quadrangle is by definition a polar space of rank two. They are the generalized n-gons with n=4...
s are exactly those partial geometries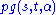 with
with  .
.

