Polaron
Encyclopedia
A polaron is a quasiparticle
composed of a charge and its accompanying polarization
field
. A slow moving electron in a dielectric
crystal
, interacting with lattice
ion
s through long-range force
s will permanently be surrounded by a region of lattice polarization
and deformation caused by the moving electron. Moving through the crystal, the electron carries the lattice distortion with it, thus one speaks of a cloud of phonon
s accompanying the electron.
The resulting lattice polarization acts as a potential well
that hinders the movements of the charge
, thus decreasing its mobility. Polarons have spin
, though two close-by polarons are spinless. The latter is called a bipolaron
.
In materials science
and chemistry
, a polaron is formed when a charge within a molecular chain influences the local nuclear
geometry, causing an attenuation (or even reversal) of nearby bond alternation amplitudes. This "excited state
" possesses an energy level between the lower and upper bands.
The polaron, a fermion
ic quasiparticle, should not be confused with the polariton
, a boson
ic quasiparticle, corresponding, e.g., to a hybridized state between a photon and an optical phonon.
theory describes the phenomenon by the induction of a polarization around the charge carrier. The induced polarization will follow the charge carrier when it is moving through the medium. The carrier together with the induced polarization is considered as one entity, which is called a polaron (see Fig. 1).
A conduction electron in an ionic crystal or a polar semiconductor is the prototype of a polaron. Herbert Fröhlich
proposed a model Hamiltonian
for this polaron through which its dynamics are treated quantum mechanically (Fröhlich Hamiltonian). If the spatial extension of a polaron is large compared to the lattice parameter of the solid, the latter can be treated as a polarizable continuum. This is the case of a large a.k.a. Fröhlich polaron. When the self-induced polarization caused by an electron or hole becomes of the order of the lattice parameter, a small a.k.a. Holstein polaron can arise. As distinct from large polarons, small polarons are governed by short-range interactions.
The polarization, carried by the longitudinal optical (LO) phonons, is represented by a set of quantum oscillators with frequency ω, the long-wavelength LO-phonon frequency, and the interaction between the charge and the polarization field is linear in the field. This model (which up to now has not been solved exactly) has been the subject of extensive investigations.
The strength of the electron-phonon interaction is expressed by a dimensionless coupling constant α introduced by Fröhlich. In Table 1 the Fröhlich coupling constant is given for a few solids.
The physical properties of a polaron differ from those of a band-carrier. A polaron is characterized by its self-energy
, an effective mass 
and by its characteristic response to external electric and magnetic fields (e. g. dc mobility and optical absorption coefficient).
When the coupling is weak (
small), the self-energy of the polaron can be approximated as :
and the polaron mass
, which can be measured by cyclotron resonance experiments, is larger than the band mass m of the charge carrier without self-induced polarization :
When the coupling is strong (α large), a variational approach due to Landau and Pekar indicates that the self-energy is proportional to α² and the polaron mass scales as α⁴. The Landau-Pekar variational calculation
yields an upper bound to the polaron self-energy
, valid
for all α, where
is a constant determined by solving an integro-differential equation. It was an open question for many years whether this
expression was asymptotically exact as α tends to infinity. Finally,
Donsker and Varadhan, applying large deviation theory to Feynman's
path integral formulation for the self-energy, showed the large α exactitude
of this Landau-Pekar formula. Later, Lieb and Thomas
gave a shorter proof using more conventional methods,
and with explicit bounds on the lower order corrections to the
Landau-Pekar formula.
Feynman
introduced a variational principle
for path integrals to study the polaron. He simulated the interaction between the electron and the polarization modes by a harmonic interaction between a hypothetical particle and the electron. The analysis of an exactly solvable ("symmetrical") 1D-polaron model, Monte Carlo schemes and other numerical schemes demonstrate the remarkable accuracy of Feynman's path-integral approach to the polaron ground-state energy. Experimentally more directly accessible properties of the polaron, such as its mobility and optical absorption, have been investigated subsequently.
Here,
is the cyclotron frequency for a rigid-band electron. The magnetooptical absorption Γ(Ω) at the frequency Ω takes the form Σ(Ω) is the so-called "memory function", which describes the dynamics of the polaron. Σ(Ω) depends also on α, β what is beta? and 
.
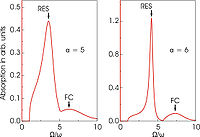
In the absence of an external magnetic field (
) the optical absorption spectrum (3) of the polaron at weak coupling is determined by the absorption of radiation energy, which is reemitted in the form of LO phonons. At larger coupling, 
, the polaron can undergo transitions toward a relatively stable internal excited state called the "relaxed excited state" (RES) (see Fig. 2). The RES peak in the spectrum also has a phonon sideband, which is related to a Franck-Condon-type transition.
A comparison of the DSG results with the optical conductivity
spectra given by approximation-free numerical and approximate analytical approaches is given in ref.
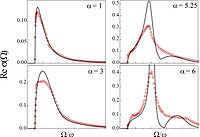
Calculations of the optical conductivity
for the Fröhlich polaron performed within the Diagrammatic Quantum Monte Carlo method, see Fig. 3, fully confirm the results of the path-integral variational approach at
In the intermediate coupling regime 
the low-energy behavior and the position of the maximum of the optical conductivity
spectrum of ref. follow well the prediction of ref. There are the following qualitative differences between the two approaches in the intermediate and strong coupling regime: in ref., the dominant peak broadens and the second peak does not develop, giving instead rise to a flat shoulder in the optical conductivity
spectrum at
. This behavior can be attributed to the optical processes with participation of two or more phonons. The nature of the excited states of a polaron needs further study.
The application of a sufficiently strong external magnetic field allows one to satisfy the resonance condition 
, which {(for 
)} determines the polaron cyclotron resonance frequency. From this condition also the polaron cyclotron mass can be derived. Using the most accurate theoretical polaron models to evaluate 
, the experimental cyclotron data can be well accounted for.
Evidence for the polaron character of charge carriers in AgBr and AgCl was obtained through high-precision cyclotron resonance experiments in external magnetic fields up to 16 T. The all-coupling magneto-absorption calculated in ref., leads to the best quantitative agreement between theory and experiment for AgBr and AgCl. This quantitative interpretation of the cyclotron resonance experiment in AgBr and
AgCl by the theory of ref. provided one of the most convincing and clearest demonstrations of Fröhlich polaron features in solids.
Experimental data on the magnetopolaron effect, obtained using far-infrared photoconductivity techniques, have been applied to study the energy spectrum of shallow donors in polar semiconductor layers of CdTe.
The polaron effect well above the LO phonon energy was studied through cyclotron resonance measurements, e. g., in II-VI semiconductors, observed in ultra-high magnetic fields. The resonant polaron effect manifests itself when the cyclotron frequency approaches the LO phonon energy in sufficiently high magnetic fields.
It has been shown that simple scaling relations exist, connecting the physical properties of polarons in 2D with those in 3D. An example of such a scaling relation is :
where
(
) and 
(
) are, respectively, the polaron and the electron-band masses in 2D (3D).
The effect of the confinement of a Fröhlich polaron is to enhance the effective polaron coupling. However, many-particle effects tend to counterbalance this effect because of screening.
Also in 2D systems cyclotron resonance is a convenient tool to study polaron effects. Although several other effects have to be taken into account (nonparabolicity of the electron bands, many-body effects, the nature of the confining potential, etc.), the polaron effect is clearly revealed in the cyclotron mass. An interesting 2D system consists of electrons on films of liquid He. In this system the electrons couple to the ripplons of the liquid He, forming "ripplopolarons". The effective coupling can be relatively large and, for some values of the parameters, self-trapping can result. The acoustic nature of the ripplon dispersion at long wavelengths is a key aspect of the trapping.
For GaAs/AlxGa1-xAs quantum wells and superlattices, the polaron effect is found to decrease the energy of the shallow donor states at low magnetic fields and leads to a resonant splitting of the energies at high magnetic fields. The energy spectra of such polaronic systems as shallow donors ("bound polarons"), e. g., the D0 and D- centres, constitute the most complete and detailed polaron spectroscopy realised in the literature.
In GaAs/AlAs quantum wells with sufficiently high electron density, anticrossing of the cyclotron-resonance spectra has been observed near the GaAs transverse optical (TO) phonon frequency rather than near the GaAs LO-phonon frequency. This anticrossing near the TO-phonon frequency was explained in the framework of the polaron theory.
Besides optical properties, many other physical properties of polarons have been studied, including the possibility of self-trapping, polaron transport, magnetophonon resonance, etc.
polaron, molecular polaron, solvated polarons, polaronic exciton, Jahn-Teller polaron, small polaron, bipolaron
s and many-polaron systems. These extensions of the concept are invoked, e. g., to study the properties of conjugated polymers, colossal magnetoresistance perovskites, high-
superconductors, layered MgB2 superconductors, fullerenes, quasi-1D conductors, semiconductor nanostructures.
The possibility that polarons and bipolarons play a role in high-
superconductors has renewed interest in the physical properties of many-polaron systems and, in particular, in their optical properties. Theoretical treatments have been extended from one-polaron to many-polaron systems.
A new aspect of the polaron concept has been investigated for semiconductor nanostructures: the exciton-phonon states are not factorizable into an adiabatic product Ansatz, so that a non-adiabatic treatment is needed. The non-adiabaticity of the exciton-phonon systems leads to a strong enhancement of the phonon-assisted transition probabilities (as compared to those treated adiabatically) and to multiphonon optical spectra that are considerably different from the Franck-Condon progression even for small values of the electron-phonon coupling constant as is the case for typical semiconductor nanostructures.
In biophysics Davydov soliton
is a propagating along the protein
α-helix self-trapped amide I excitation that is a solution of the Davydov Hamiltonian. The mathematical techniques that are used to analyze Davydov's soliton are similar to some that have been developed in polaron theory. In this context the Davydov soliton
corresponds to a polaron that is (i) large so the continuum limit approximation in justified, (ii) acoustic because the self-localization arises from interactions with acoustic modes of the lattice, and (iii) weakly coupled because the anharmonic energy is small compared with the phonon bandwidth.
More recently it was shown that the system of an impurity in a Bose-Einstein condensate is also a member of the polaron family. This is very promising for experimentally probing the hitherto inaccessible strong coupling regime since in this case interaction strengths can be externally tuned through the use of a Feshbach resonance
.
Quasiparticle
In physics, quasiparticles are emergent phenomena that occur when a microscopically complicated system such as a solid behaves as if it contained different weakly interacting particles in free space...
composed of a charge and its accompanying polarization
Polarization density
In classical electromagnetism, polarization density is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is...
field
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
. A slow moving electron in a dielectric
Dielectric
A dielectric is an electrical insulator that can be polarized by an applied electric field. When a dielectric is placed in an electric field, electric charges do not flow through the material, as in a conductor, but only slightly shift from their average equilibrium positions causing dielectric...
crystal
Crystal
A crystal or crystalline solid is a solid material whose constituent atoms, molecules, or ions are arranged in an orderly repeating pattern extending in all three spatial dimensions. The scientific study of crystals and crystal formation is known as crystallography...
, interacting with lattice
Crystal structure
In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
ion
Ion
An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
s through long-range force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
s will permanently be surrounded by a region of lattice polarization
Polarization density
In classical electromagnetism, polarization density is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is placed in an external electric field, its molecules gain electric dipole moment and the dielectric is...
and deformation caused by the moving electron. Moving through the crystal, the electron carries the lattice distortion with it, thus one speaks of a cloud of phonon
Phonon
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...
s accompanying the electron.
The resulting lattice polarization acts as a potential well
Potential well
A potential well is the region surrounding a local minimum of potential energy. Energy captured in a potential well is unable to convert to another type of energy because it is captured in the local minimum of a potential well...
that hinders the movements of the charge
Charge (physics)
In physics, a charge may refer to one of many different quantities, such as the electric charge in electromagnetism or the color charge in quantum chromodynamics. Charges are associated with conserved quantum numbers.-Formal definition:...
, thus decreasing its mobility. Polarons have spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
, though two close-by polarons are spinless. The latter is called a bipolaron
Bipolaron
- Bipolarons in physics :In physics, a bipolaron is a bound pair of two polarons. An electron in a material may cause a distortion in the underlying lattice. The combination of electron and distortion is known as a polaron...
.
In materials science
Materials science
Materials science is an interdisciplinary field applying the properties of matter to various areas of science and engineering. This scientific field investigates the relationship between the structure of materials at atomic or molecular scales and their macroscopic properties. It incorporates...
and chemistry
Chemistry
Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
, a polaron is formed when a charge within a molecular chain influences the local nuclear
Atomic nucleus
The nucleus is the very dense region consisting of protons and neutrons at the center of an atom. It was discovered in 1911, as a result of Ernest Rutherford's interpretation of the famous 1909 Rutherford experiment performed by Hans Geiger and Ernest Marsden, under the direction of Rutherford. The...
geometry, causing an attenuation (or even reversal) of nearby bond alternation amplitudes. This "excited state
Excited state
Excitation is an elevation in energy level above an arbitrary baseline energy state. In physics there is a specific technical definition for energy level which is often associated with an atom being excited to an excited state....
" possesses an energy level between the lower and upper bands.
The polaron, a fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
ic quasiparticle, should not be confused with the polariton
Polariton
In physics, polaritons are quasiparticles resulting from strong coupling of electromagnetic waves with an electric or magnetic dipole-carrying excitation. They are an expression of the common quantum phenomenon known as level repulsion, also known as the anti-crossing principle...
, a boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
ic quasiparticle, corresponding, e.g., to a hybridized state between a photon and an optical phonon.
Polaron theory
L. D. Landau and S. I. Pekar formed the basis of polaron theory. A charge placed in a polarizable medium will be screened. DielectricDielectric
A dielectric is an electrical insulator that can be polarized by an applied electric field. When a dielectric is placed in an electric field, electric charges do not flow through the material, as in a conductor, but only slightly shift from their average equilibrium positions causing dielectric...
theory describes the phenomenon by the induction of a polarization around the charge carrier. The induced polarization will follow the charge carrier when it is moving through the medium. The carrier together with the induced polarization is considered as one entity, which is called a polaron (see Fig. 1).
| Material | α | Material | α |
|---|---|---|---|
| InSb | 0.023 | KI | 2.5 |
| InAs | 0.052 | TlBr | 2.55 |
| GaAs | 0.068 | KBr | 3.05 |
| GaP | 0.20 | RbI | 3.16 |
| CdTe | 0.29 | Bi12SiO20 | 3.18 |
| ZnSe | 0.43 | CdF2 | 3.2 |
| CdS | 0.53 | KCl | 3.44 |
| AgBr | 1.53 | CsI | 3.67 |
| AgCl | 1.84 | SrTiO3 | 3.77 |
| α-Al2O3 | 2.40 | RbCl | 3.81 |
A conduction electron in an ionic crystal or a polar semiconductor is the prototype of a polaron. Herbert Fröhlich
Herbert Fröhlich
Herbert Fröhlich was a German-born British physicist and a Fellow of the Royal Society....
proposed a model Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
for this polaron through which its dynamics are treated quantum mechanically (Fröhlich Hamiltonian). If the spatial extension of a polaron is large compared to the lattice parameter of the solid, the latter can be treated as a polarizable continuum. This is the case of a large a.k.a. Fröhlich polaron. When the self-induced polarization caused by an electron or hole becomes of the order of the lattice parameter, a small a.k.a. Holstein polaron can arise. As distinct from large polarons, small polarons are governed by short-range interactions.
The polarization, carried by the longitudinal optical (LO) phonons, is represented by a set of quantum oscillators with frequency ω, the long-wavelength LO-phonon frequency, and the interaction between the charge and the polarization field is linear in the field. This model (which up to now has not been solved exactly) has been the subject of extensive investigations.
The strength of the electron-phonon interaction is expressed by a dimensionless coupling constant α introduced by Fröhlich. In Table 1 the Fröhlich coupling constant is given for a few solids.
The physical properties of a polaron differ from those of a band-carrier. A polaron is characterized by its self-energy
, an effective mass and by its characteristic response to external electric and magnetic fields (e. g. dc mobility and optical absorption coefficient).When the coupling is weak (
small), the self-energy of the polaron can be approximated as : |
 |
and the polaron mass
, which can be measured by cyclotron resonance experiments, is larger than the band mass m of the charge carrier without self-induced polarization : |
 |
When the coupling is strong (α large), a variational approach due to Landau and Pekar indicates that the self-energy is proportional to α² and the polaron mass scales as α⁴. The Landau-Pekar variational calculation
yields an upper bound to the polaron self-energy
, validfor all α, where
is a constant determined by solving an integro-differential equation. It was an open question for many years whether thisexpression was asymptotically exact as α tends to infinity. Finally,
Donsker and Varadhan, applying large deviation theory to Feynman's
path integral formulation for the self-energy, showed the large α exactitude
of this Landau-Pekar formula. Later, Lieb and Thomas
gave a shorter proof using more conventional methods,
and with explicit bounds on the lower order corrections to the
Landau-Pekar formula.
Feynman
Feynman
Feynman may refer to:* Richard Feynman , physicist** Feynman diagram** Feynman graph** Feynman–Kac formula** The Feynman Lectures on Physics** Feynman integral, see Path integral formulation** Feynman parametrization...
introduced a variational principle
Variational principle
A variational principle is a scientific principle used within the calculus of variations, which develops general methods for finding functions which minimize or maximize the value of quantities that depend upon those functions...
for path integrals to study the polaron. He simulated the interaction between the electron and the polarization modes by a harmonic interaction between a hypothetical particle and the electron. The analysis of an exactly solvable ("symmetrical") 1D-polaron model, Monte Carlo schemes and other numerical schemes demonstrate the remarkable accuracy of Feynman's path-integral approach to the polaron ground-state energy. Experimentally more directly accessible properties of the polaron, such as its mobility and optical absorption, have been investigated subsequently.
Polaron optical absorption
The expression for the magnetooptical absorption of a polaron is : |
 |
Here,
is the cyclotron frequency for a rigid-band electron. The magnetooptical absorption Γ(Ω) at the frequency Ω takes the form Σ(Ω) is the so-called "memory function", which describes the dynamics of the polaron. Σ(Ω) depends also on α, β what is beta? and .In the absence of an external magnetic field (
) the optical absorption spectrum (3) of the polaron at weak coupling is determined by the absorption of radiation energy, which is reemitted in the form of LO phonons. At larger coupling, , the polaron can undergo transitions toward a relatively stable internal excited state called the "relaxed excited state" (RES) (see Fig. 2). The RES peak in the spectrum also has a phonon sideband, which is related to a Franck-Condon-type transition.Optical conductivity
Optical conductivity is one of the powerful tools for studying the electronic states in materials.If a system is subjected to an external electric field then, in general, a redistribution of charges occurs and currents are induced. For small enough fields, the induced polarization and the induced...
spectra given by approximation-free numerical and approximate analytical approaches is given in ref.
Calculations of the optical conductivity
Optical conductivity
Optical conductivity is one of the powerful tools for studying the electronic states in materials.If a system is subjected to an external electric field then, in general, a redistribution of charges occurs and currents are induced. For small enough fields, the induced polarization and the induced...
for the Fröhlich polaron performed within the Diagrammatic Quantum Monte Carlo method, see Fig. 3, fully confirm the results of the path-integral variational approach at
In the intermediate coupling regime the low-energy behavior and the position of the maximum of the optical conductivityOptical conductivity
Optical conductivity is one of the powerful tools for studying the electronic states in materials.If a system is subjected to an external electric field then, in general, a redistribution of charges occurs and currents are induced. For small enough fields, the induced polarization and the induced...
spectrum of ref. follow well the prediction of ref. There are the following qualitative differences between the two approaches in the intermediate and strong coupling regime: in ref., the dominant peak broadens and the second peak does not develop, giving instead rise to a flat shoulder in the optical conductivity
Optical conductivity
Optical conductivity is one of the powerful tools for studying the electronic states in materials.If a system is subjected to an external electric field then, in general, a redistribution of charges occurs and currents are induced. For small enough fields, the induced polarization and the induced...
spectrum at
. This behavior can be attributed to the optical processes with participation of two or more phonons. The nature of the excited states of a polaron needs further study., which {(for )} determines the polaron cyclotron resonance frequency. From this condition also the polaron cyclotron mass can be derived. Using the most accurate theoretical polaron models to evaluate , the experimental cyclotron data can be well accounted for.Evidence for the polaron character of charge carriers in AgBr and AgCl was obtained through high-precision cyclotron resonance experiments in external magnetic fields up to 16 T. The all-coupling magneto-absorption calculated in ref., leads to the best quantitative agreement between theory and experiment for AgBr and AgCl. This quantitative interpretation of the cyclotron resonance experiment in AgBr and
AgCl by the theory of ref. provided one of the most convincing and clearest demonstrations of Fröhlich polaron features in solids.
Experimental data on the magnetopolaron effect, obtained using far-infrared photoconductivity techniques, have been applied to study the energy spectrum of shallow donors in polar semiconductor layers of CdTe.
The polaron effect well above the LO phonon energy was studied through cyclotron resonance measurements, e. g., in II-VI semiconductors, observed in ultra-high magnetic fields. The resonant polaron effect manifests itself when the cyclotron frequency approaches the LO phonon energy in sufficiently high magnetic fields.
Polarons in two dimensions and in quasi-2D structures
The great interest in the study of the two-dimensional electron gas (2DEG) has also resulted in many investigations on the properties of polarons in two dimensions. A simple model for the 2D polaron system consists of an electron confined to a plane, interacting via the Fröhlich interaction with the LO phonons of a 3D surrounding medium. The self-energy and the mass of such a 2D polaron are no longer described by the expressions valid in 3D; for weak coupling they can be approximated as : |
 |
 |
 |
It has been shown that simple scaling relations exist, connecting the physical properties of polarons in 2D with those in 3D. An example of such a scaling relation is :
 |
 |
where
() and () are, respectively, the polaron and the electron-band masses in 2D (3D).The effect of the confinement of a Fröhlich polaron is to enhance the effective polaron coupling. However, many-particle effects tend to counterbalance this effect because of screening.
Also in 2D systems cyclotron resonance is a convenient tool to study polaron effects. Although several other effects have to be taken into account (nonparabolicity of the electron bands, many-body effects, the nature of the confining potential, etc.), the polaron effect is clearly revealed in the cyclotron mass. An interesting 2D system consists of electrons on films of liquid He. In this system the electrons couple to the ripplons of the liquid He, forming "ripplopolarons". The effective coupling can be relatively large and, for some values of the parameters, self-trapping can result. The acoustic nature of the ripplon dispersion at long wavelengths is a key aspect of the trapping.
For GaAs/AlxGa1-xAs quantum wells and superlattices, the polaron effect is found to decrease the energy of the shallow donor states at low magnetic fields and leads to a resonant splitting of the energies at high magnetic fields. The energy spectra of such polaronic systems as shallow donors ("bound polarons"), e. g., the D0 and D- centres, constitute the most complete and detailed polaron spectroscopy realised in the literature.
In GaAs/AlAs quantum wells with sufficiently high electron density, anticrossing of the cyclotron-resonance spectra has been observed near the GaAs transverse optical (TO) phonon frequency rather than near the GaAs LO-phonon frequency. This anticrossing near the TO-phonon frequency was explained in the framework of the polaron theory.
Besides optical properties, many other physical properties of polarons have been studied, including the possibility of self-trapping, polaron transport, magnetophonon resonance, etc.
Extensions of the polaron concept
Significant are also the extensions of the polaron concept: acoustic polaron, piezoelectric polaron, electronic polaron, bound polaron, trapped polaron, spinSpin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
polaron, molecular polaron, solvated polarons, polaronic exciton, Jahn-Teller polaron, small polaron, bipolaron
Bipolaron
- Bipolarons in physics :In physics, a bipolaron is a bound pair of two polarons. An electron in a material may cause a distortion in the underlying lattice. The combination of electron and distortion is known as a polaron...
s and many-polaron systems. These extensions of the concept are invoked, e. g., to study the properties of conjugated polymers, colossal magnetoresistance perovskites, high-
superconductors, layered MgB2 superconductors, fullerenes, quasi-1D conductors, semiconductor nanostructures.The possibility that polarons and bipolarons play a role in high-
superconductors has renewed interest in the physical properties of many-polaron systems and, in particular, in their optical properties. Theoretical treatments have been extended from one-polaron to many-polaron systems.A new aspect of the polaron concept has been investigated for semiconductor nanostructures: the exciton-phonon states are not factorizable into an adiabatic product Ansatz, so that a non-adiabatic treatment is needed. The non-adiabaticity of the exciton-phonon systems leads to a strong enhancement of the phonon-assisted transition probabilities (as compared to those treated adiabatically) and to multiphonon optical spectra that are considerably different from the Franck-Condon progression even for small values of the electron-phonon coupling constant as is the case for typical semiconductor nanostructures.
In biophysics Davydov soliton
Davydov soliton
Davydov soliton is a quantum quasiparticle representing an excitation propagating along the protein α-helix self-trapped amide I. It is a solution of the Davydov Hamiltonian. It is named for the Soviet and Ukrainian physicist Alexander Davydov. The Davydov model describes the interaction of the...
is a propagating along the protein
Protein
Proteins are biochemical compounds consisting of one or more polypeptides typically folded into a globular or fibrous form, facilitating a biological function. A polypeptide is a single linear polymer chain of amino acids bonded together by peptide bonds between the carboxyl and amino groups of...
α-helix self-trapped amide I excitation that is a solution of the Davydov Hamiltonian. The mathematical techniques that are used to analyze Davydov's soliton are similar to some that have been developed in polaron theory. In this context the Davydov soliton
Davydov soliton
Davydov soliton is a quantum quasiparticle representing an excitation propagating along the protein α-helix self-trapped amide I. It is a solution of the Davydov Hamiltonian. It is named for the Soviet and Ukrainian physicist Alexander Davydov. The Davydov model describes the interaction of the...
corresponds to a polaron that is (i) large so the continuum limit approximation in justified, (ii) acoustic because the self-localization arises from interactions with acoustic modes of the lattice, and (iii) weakly coupled because the anharmonic energy is small compared with the phonon bandwidth.
More recently it was shown that the system of an impurity in a Bose-Einstein condensate is also a member of the polaron family. This is very promising for experimentally probing the hitherto inaccessible strong coupling regime since in this case interaction strengths can be externally tuned through the use of a Feshbach resonance
Feshbach resonance
In physics, Feshbach resonance, named after Herman Feshbach, is a resonance of a many-body system in which a bound state is achieved if the coupling between an internal degree of freedom and the reaction coordinates which lead to dissociation vanish...
.