Polynomial code
Encyclopedia
In coding theory
, a polynomial code is a type of linear code
whose set of valid code words consists of those polynomials (usually of some fixed length) that are divisible
by a given fixed polynomial (of shorter length, called the generator polynomial).
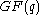, whose elements we call symbols. For the purposes of constructing polynomial codes, we identify a string of 
symbols 
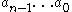with the polynomial
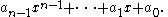
Fix integers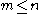
and let 
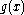be some fixed polynomial of degree 
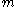, called the generator polynomial. The polynomial code generated by 
is the code whose code words are precisely the polynomials of degree less than 
that are divisible
(without remainder) by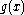
.
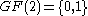with 
, 
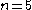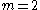, and generator polynomial 
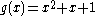. This code consists of the following code words:
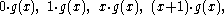
Or written explicitly:
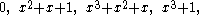
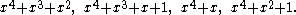
Equivalently, expressed as strings of binary digits, the codewords are:
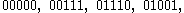
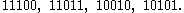
Note that this, as every polynomial code, is indeed a linear code
, i.e., linear combinations of code words are again code words. In a case like this where the field is GF(2), linear combinations are found by taking the XOR of the codewords expressed in binary form (e.g. 00111 XOR 10010 = 10101).
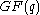with code length 
and generator polynomial 
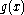of degree 
,
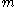there will be exactly
code words. Indeed, by definition, 
is a code word if and only if it is of the form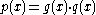 
, where 
(the quotient) is of degree less than 
. Since there are 
such quotients available, there is the same number of possible code words.
Plain (unencoded) data words should therefore be of length
Some authors, such as (Lidl & Pilz, 1999), only discuss the mapping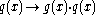
as the assignment from data words to code words. However, this has the disadvantage that the data word does not appear as part of the code word.
Instead, the following method is often used to create a systematic code
: given a data word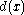
of length 
, first multiply 
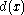by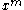 
, which has the effect of shifting 
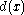by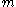 
places to the left. In general, 
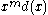will not be divisible by 
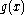, i.e., it will not be a valid code word. However, there is a unique code word that can be obtained by adjusting the rightmost 
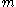symbols of 
.
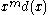To calculate it, compute the remainder of dividing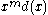
by 
:
where
is of degree less than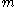 
. The code word corresponding to the data word 
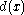is then defined to be
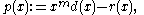
Note the following properties:
, 
, and generator polynomial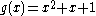 
, we obtain the following assignment from data words to codewords:
Assuming that the code word is free of errors, a systematic code can be decoded simply by stripping away the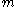
checksum digits.
If there are errors, then error correction should be performed before decoding. Efficient decoding algorithms exist for specific polynomial codes, such as BCH code
s.
abilities of polynomial codes are determined by the minimum Hamming distance
of the code. Since polynomial codes are linear codes, the minimum Hamming distance is equal to the minimum weight of any non-zero codeword. In the example above, the minimum Hamming distance is 2, since 01001 is a codeword, and there is no nonzero codeword with only one bit set.
More specific properties of a polynomial code often depend on particular algebraic properties of its generator polynomial. Here are some examples of such properties:
The algebraic nature of polynomial codes, with cleverly chosen generator polynomials, can also often be exploited to find efficient error correction algorithms. This is the case for BCH code
s.
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, a polynomial code is a type of linear code
Linear code
In coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although Turbo codes can be seen as a hybrid of these two types. Linear codes allow for...
whose set of valid code words consists of those polynomials (usually of some fixed length) that are divisible
Polynomial long division
In algebra, polynomial long division is an algorithm for dividing a polynomial by another polynomial of the same or lower degree, a generalised version of the familiar arithmetic technique called long division...
by a given fixed polynomial (of shorter length, called the generator polynomial).
Definition
Fix a finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
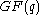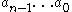, whose elements we call symbols. For the purposes of constructing polynomial codes, we identify a string of symbols with the polynomial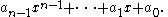Fix integers
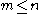and let 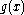be some fixed polynomial of degree 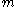, called the generator polynomial. The polynomial code generated by is the code whose code words are precisely the polynomials of degree less than that are divisiblePolynomial long division
In algebra, polynomial long division is an algorithm for dividing a polynomial by another polynomial of the same or lower degree, a generalised version of the familiar arithmetic technique called long division...
(without remainder) by
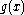.Example
Consider the polynomial code over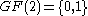 with 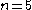, , 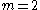and generator polynomial 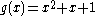. This code consists of the following code words: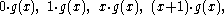Or written explicitly:
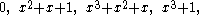
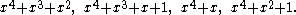
Equivalently, expressed as strings of binary digits, the codewords are:
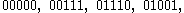
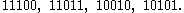
Note that this, as every polynomial code, is indeed a linear code
Linear code
In coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although Turbo codes can be seen as a hybrid of these two types. Linear codes allow for...
, i.e., linear combinations of code words are again code words. In a case like this where the field is GF(2), linear combinations are found by taking the XOR of the codewords expressed in binary form (e.g. 00111 XOR 10010 = 10101).
Encoding
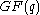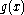In a polynomial code over with code length and generator polynomial of degree 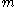,there will be exactly
code words. Indeed, by definition, is a code word if and only if it is of the form 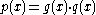, where (the quotient) is of degree less than . Since there are such quotients available, there is the same number of possible code words.Plain (unencoded) data words should therefore be of length
Some authors, such as (Lidl & Pilz, 1999), only discuss the mapping
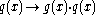as the assignment from data words to code words. However, this has the disadvantage that the data word does not appear as part of the code word.Instead, the following method is often used to create a systematic code
Systematic code
In coding theory, a systematic code is any error-correcting code in which the input data is embedded in the encoded output. Conversely, in a non-systematic code the output does not contain the input symbols....
: given a data word
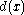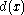of length , first multiply by 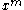, which has the effect of shifting 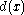by 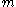places to the left. In general, 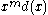will not be divisible by 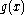, i.e., it will not be a valid code word. However, there is a unique code word that can be obtained by adjusting the rightmost 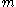symbols of 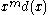.To calculate it, compute the remainder of dividing
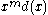by :where
is of degree less than 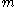. The code word corresponding to the data word 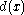is then defined to be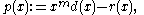Note the following properties:
-
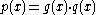, which is divisible by 
. In particular, 
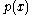is a valid code word. - Since
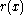is of degree less than 
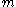, the leftmost 
symbols of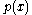 
agree with the corresponding symbols of 
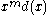. In other words, the first 
symbols of the code word are the same as the original data word. The remaining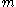 
symbols are called checksum digits or check bits.
Example
For the above code with, , and generator polynomial 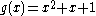, we obtain the following assignment from data words to codewords:- 000 00000
- 001 00111
- 010 01001
- 011 01110
- 100 10010
- 101 10101
- 110 11011
- 111 11100
Decoding
An erroneous message can by detected in a straightforward way through polynomial division by the generator polynomial resulting in a non-zero remainder.Assuming that the code word is free of errors, a systematic code can be decoded simply by stripping away the
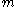checksum digits.If there are errors, then error correction should be performed before decoding. Efficient decoding algorithms exist for specific polynomial codes, such as BCH code
BCH code
In coding theory the BCH codes form a class of parameterised error-correcting codes which have been the subject of much academic attention in the last fifty years. BCH codes were invented in 1959 by Hocquenghem, and independently in 1960 by Bose and Ray-Chaudhuri...
s.
Properties of polynomial codes
As for all digital codes, the error detection and correctionError detection and correction
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction or error control are techniques that enable reliable delivery of digital data over unreliable communication channels...
abilities of polynomial codes are determined by the minimum Hamming distance
Hamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
of the code. Since polynomial codes are linear codes, the minimum Hamming distance is equal to the minimum weight of any non-zero codeword. In the example above, the minimum Hamming distance is 2, since 01001 is a codeword, and there is no nonzero codeword with only one bit set.
More specific properties of a polynomial code often depend on particular algebraic properties of its generator polynomial. Here are some examples of such properties:
- A polynomial code is cyclic if and only if the generator polynomial divides
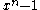. - If the generator polynomial is primitivePrimitive polynomialIn field theory, a branch of mathematics, a primitive polynomial is the minimal polynomial of a primitive element of the finite extension field GF...
, then the resulting code has Hamming distance at least 3, provided that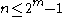
. - In BCH codeBCH codeIn coding theory the BCH codes form a class of parameterised error-correcting codes which have been the subject of much academic attention in the last fifty years. BCH codes were invented in 1959 by Hocquenghem, and independently in 1960 by Bose and Ray-Chaudhuri...
s, the generator polynomial is chosen to have specific roots in an extension field, in a way that achieves high Hamming distance.
The algebraic nature of polynomial codes, with cleverly chosen generator polynomials, can also often be exploited to find efficient error correction algorithms. This is the case for BCH code
BCH code
In coding theory the BCH codes form a class of parameterised error-correcting codes which have been the subject of much academic attention in the last fifty years. BCH codes were invented in 1959 by Hocquenghem, and independently in 1960 by Bose and Ray-Chaudhuri...
s.
Specific families of polynomial codes
- Cyclic codes – every cyclic code is also a polynomial code; a popular example is the CRCCyclic redundancy checkA cyclic redundancy check is an error-detecting code commonly used in digital networks and storage devices to detect accidental changes to raw data...
code. - BCH codeBCH codeIn coding theory the BCH codes form a class of parameterised error-correcting codes which have been the subject of much academic attention in the last fifty years. BCH codes were invented in 1959 by Hocquenghem, and independently in 1960 by Bose and Ray-Chaudhuri...
s – a family of cyclic codes with high Hamming distance and efficient algebraic error correction algorithms. - Reed-Solomon codes – an important subset of BCH codes with particularly efficient structure.