
Poset game
Encyclopedia
Poset games are mathematical
games of strategy where, given a poset P, two players alternate on choosing one point in P, removing it and and all points that are greater. The player who is left with no point to choose, loses.
Several popular specializations exist, such as Nim
, Hackendot, Chomp
, and Hackenbush
.
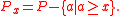
A poset game on P, played between Alice and Bob
, is as follows:
. The essential property of this theorem is the Grundy value. We define the Grundy value of a poset to be the least natural number which is not the Grundy value of any Px, x ∈ P. That is,
It is the case that any move will alter the Grundy value, and that if G(P) > 0, there must exist Px with G(Px) = 0. Since G(∅) = 0, it must be the case that Alice has a winning strategy if G(P) > 0, since she might then choose x such that G(Px) = 0, forcing Bob to choose y such that G(y) > 0.
Mathematical game
A mathematical game is a multiplayer game whose rules, strategies, and outcomes can be studied and explained by mathematics. Examples of such games are Tic-tac-toe and Dots and Boxes, to name a couple. On the surface, a game need not seem mathematical or complicated to still be a mathematical game...
games of strategy where, given a poset P, two players alternate on choosing one point in P, removing it and and all points that are greater. The player who is left with no point to choose, loses.
Several popular specializations exist, such as Nim
Nim
Nim is a mathematical game of strategy in which two players take turns removing objects from distinct heaps. On each turn, a player must remove at least one object, and may remove any number of objects provided they all come from the same heap....
, Hackendot, Chomp
Chomp
Chomp is a 2-player game of strategy played on a rectangular "chocolate bar" made up of smaller square blocks . The players take it in turns to choose one block and "eat it" , together with those that are below it and to its right...
, and Hackenbush
Hackenbush
Hackenbush is a two-player mathematical game that may be played on any configuration of colored line segments connected to one another by their endpoints and to the ground...
.
Game play
Given a poset (P, <), let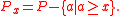
A poset game on P, played between Alice and Bob
Alice and Bob
The names Alice and Bob are commonly used placeholder names for archetypal characters in fields such as cryptography and physics. The names are used for convenience; for example, "Alice sends a message to Bob encrypted with his public key" is easier to follow than "Party A sends a message to Party...
, is as follows:
- The current player chooses a point x ∈ P, replaces P with Px, and then passes the turn.
- A player loses if it is his/her turn and there are no points to choose.
The Grundy value of poset games
Poset games are subject to the Sprague–Grundy theoremSprague–Grundy theorem
In combinatorial game theory, the Sprague–Grundy theorem states that every impartial game under the normal play convention is equivalent to a nimber. The Grundy value or nim-value of an impartial game is then defined as the unique nimber that the game is equivalent to...
. The essential property of this theorem is the Grundy value. We define the Grundy value of a poset to be the least natural number which is not the Grundy value of any Px, x ∈ P. That is,
It is the case that any move will alter the Grundy value, and that if G(P) > 0, there must exist Px with G(Px) = 0. Since G(∅) = 0, it must be the case that Alice has a winning strategy if G(P) > 0, since she might then choose x such that G(Px) = 0, forcing Bob to choose y such that G(y) > 0.


