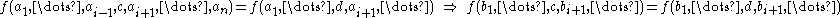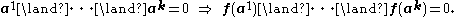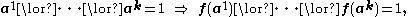Post's lattice
Encyclopedia
In logic
and universal algebra
, Post's lattice denotes the lattice
of all clone
s on a two-element set {0, 1}, ordered by inclusion. It is named for Emil Post
, who published a complete description of the lattice in 1941. The relative simplicity of Post's lattice is in stark contrast to the lattice of clones on a three-element (or larger) set, which has the cardinality of the continuum
, and a complicated inner structure. A modern exposition of Post's result can be found in Lau (2006).
, is an n-ary operation
for some , where 2 denotes the two-element set {0, 1}. Particular Boolean functions are the projections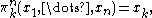
and given an m-ary function f, and n-ary functions g1, ..., gm, we can construct another n-ary function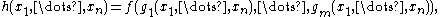
called their composition
. A set of functions closed under composition, and containing all projections, is called a clone
.
Let B be a set of connectives. The functions which can be defined by a formula using propositional variable
s and connectives from B form a clone [B], indeed it is the smallest clone which includes B. We call [B] the clone generated by B, and say that B is the basis of [B]. For example, [¬, ⋀] are all Boolean functions, and [0, 1, ⋀, ⋁] are the monotone functions.
We use the operations ¬ (negation
), ⋀ (conjunction
or meet
), ⋁ (disjunction or join), → (implication
), ↔ (biconditional
), + (exclusive disjunction
or Boolean ring
addition
), ↛ (nonimplication
), ?: (the ternary conditional operator
) and the constant unary functions 0 and 1. Moreover, we need the threshold functions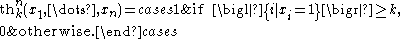
For example, th1n is the large disjunction of all the variables xi, and thnn is the large conjunction. Of particular importance is the majority function
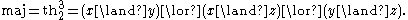
We denote elements of 2n (i.e., truth-assignments) as vectors: . The set 2n carries a natural product
Boolean algebra structure. That is, ordering, meets, joins, and other operations on n-ary truth assignments are defined pointwise: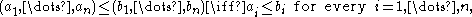
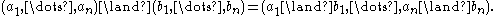
of an arbitrary number of clones is again a clone. It is convenient to denote intersection of clones by simple juxtaposition, i.e., the clone is denoted by C1C2...Ck. Some special clones are introduced below:
. The lattice is countably infinite, and all its members are finitely generated. All the clones are listed in the table below.
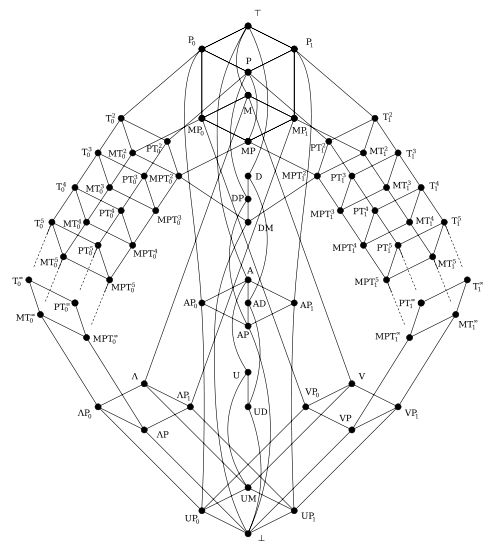
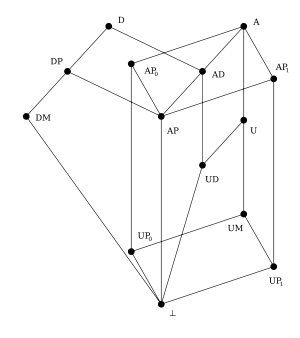
The eight infinite families have actually also members with k = 1, but these appear separately in the table: , , , , , .
The lattice has a natural symmetry mapping each clone C to its dual clone }, where is the de Morgan dual of a Boolean function f. For example, , , and .
as well as permutation and identification of variables. The main difference is that iterative systems do not necessarily contain all projections. Every clone is an iterative system, and there are 20 non-empty iterative systems which are not clones. (Post also excluded the empty iterative system from the classification, hence his diagram has no least element and fails to be a lattice.) As another alternative, some authors work with the notion of a closed class, which is an iterative system closed under introduction of dummy variables. There are four closed classes which are not clones: the empty set, the set of constant 0 functions, the set of constant 1 functions, and the set of all constant functions.
Composition alone does not allow to generate a nullary function from the corresponding unary constant function, this is the technical reason why nullary functions are excluded from clones in Post's classification. If we lift the restriction, we get more clones. Namely, each clone C in Post's lattice which contains at least one constant function corresponds to two clones under the less restrictive definition: C, and C together with all nullary functions whose unary versions are in C.
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
and universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
, Post's lattice denotes the lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
of all clone
Clone (algebra)
In universal algebra, a clone is a set C of operations on a set A such that*C contains all the projections , defined by ,*C is closed under composition : if f, g1, …, gm are members of C such that f is m-ary, and gj is n-ary for every j, then the n-ary operation is in C.Given an algebra...
s on a two-element set {0, 1}, ordered by inclusion. It is named for Emil Post
Emil Leon Post
Emil Leon Post was a mathematician and logician. He is best known for his work in the field that eventually became known as computability theory.-Early work:...
, who published a complete description of the lattice in 1941. The relative simplicity of Post's lattice is in stark contrast to the lattice of clones on a three-element (or larger) set, which has the cardinality of the continuum
Cardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
, and a complicated inner structure. A modern exposition of Post's result can be found in Lau (2006).
Basic concepts
A Boolean function, or logical connectiveLogical connective
In logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
, is an n-ary operation
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
for some , where 2 denotes the two-element set {0, 1}. Particular Boolean functions are the projections
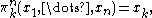
and given an m-ary function f, and n-ary functions g1, ..., gm, we can construct another n-ary function
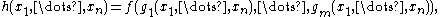
called their composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
. A set of functions closed under composition, and containing all projections, is called a clone
Clone (algebra)
In universal algebra, a clone is a set C of operations on a set A such that*C contains all the projections , defined by ,*C is closed under composition : if f, g1, …, gm are members of C such that f is m-ary, and gj is n-ary for every j, then the n-ary operation is in C.Given an algebra...
.
Let B be a set of connectives. The functions which can be defined by a formula using propositional variable
Propositional variable
In mathematical logic, a propositional variable is a variable which can either be true or false...
s and connectives from B form a clone [B], indeed it is the smallest clone which includes B. We call [B] the clone generated by B, and say that B is the basis of [B]. For example, [¬, ⋀] are all Boolean functions, and [0, 1, ⋀, ⋁] are the monotone functions.
We use the operations ¬ (negation
Negation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
), ⋀ (conjunction
Logical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
or meet
Meet (mathematics)
In mathematics, join and meet are dual binary operations on the elements of a partially ordered set. A join on a set is defined as the supremum with respect to a partial order on the set, provided a supremum exists...
), ⋁ (disjunction or join), → (implication
Material conditional
The material conditional, also known as material implication, is a binary truth function, such that the compound sentence p→q is logically equivalent to the negative compound: not . A material conditional compound itself is often simply called a conditional...
), ↔ (biconditional
Logical biconditional
In logic and mathematics, the logical biconditional is the logical connective of two statements asserting "p if and only if q", where q is a hypothesis and p is a conclusion...
), + (exclusive disjunction
Exclusive disjunction
The logical operation exclusive disjunction, also called exclusive or , is a type of logical disjunction on two operands that results in a value of true if exactly one of the operands has a value of true...
or Boolean ring
Boolean ring
In mathematics, a Boolean ring R is a ring for which x2 = x for all x in R; that is, R consists only of idempotent elements....
addition
Addition
Addition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
), ↛ (nonimplication
Material nonimplication
Material nonimplication or abjunction is the negation of implication. That is to say that for any two propositions P and Q, if P does not imply Q, then P is the material nonimplication of Q....
), ?: (the ternary conditional operator
?:
In computer programming, ?: is a ternary operator that is part of the syntax for a basic conditional expression in several programming languages...
) and the constant unary functions 0 and 1. Moreover, we need the threshold functions
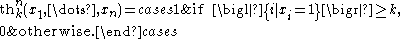
For example, th1n is the large disjunction of all the variables xi, and thnn is the large conjunction. Of particular importance is the majority function
Majority function
In Boolean logic, the majority function is a function from n inputs to one output. The value of the operation is false when n/2 or more arguments are false, and true otherwise....
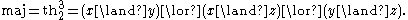
We denote elements of 2n (i.e., truth-assignments) as vectors: . The set 2n carries a natural product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
Boolean algebra structure. That is, ordering, meets, joins, and other operations on n-ary truth assignments are defined pointwise:
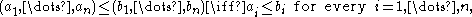
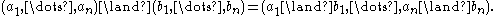
Naming of clones
IntersectionIntersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of an arbitrary number of clones is again a clone. It is convenient to denote intersection of clones by simple juxtaposition, i.e., the clone is denoted by C1C2...Ck. Some special clones are introduced below:
- M is the set of monotone functions: for every .
- D is the set of self-dual functions: .
- A is the set of affineAffine transformationIn geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
functions: the functions satisfying
-
- for every i ≤ n, a, b ∈ 2n, and c, d ∈ 2. Equivalently, the functions expressible as for some a0, a.
- U is the set of essentially unary functions, i.e., functions which depend on at most one input variable: there exists an i = 1, ..., n such that whenever .
- Λ is the set of conjunctive functions: . The clone Λ consists of the conjunctions
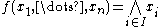for all subsets I of {1, ..., n} (including the empty conjunction, i.e., the constant 1), and the constant 0. - V is the set of disjunctive functions: . Equivalently, V consists of the disjunctions
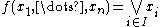for all subsets I of {1, ..., n} (including the empty disjunction 0), and the constant 1. - For any k ≥ 1, T0k is the set of functions f such that
- Moreover,
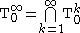is the set of functions bounded above by a variable: there exists i = 1, ..., n such that for all a. - As a special case, is the set of 0-preserving functions: .
- For any k ≥ 1, T1k is the set of functions f such that
- and
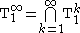is the set of functions bounded below by a variable: there exists i = 1, ..., n such that for all a. - The special case consists of the 1-preserving functions: .
- The largest clone of all functions is denoted ⊤, the smallest clone (which contains only projections) is denoted ⊥, and is the clone of constant-preserving functions.
Lattice
The set of all clones is a closure system, hence it forms a complete latticeComplete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
. The lattice is countably infinite, and all its members are finitely generated. All the clones are listed in the table below.
| clone | one of its bases |
|---|---|
| ⊤ | ⋁, ¬ |
| P0 | ⋁, + |
| P1 | ⋀, → |
| P | ?: |
| T0k, k ≥ 2 | thkk+1, ↛ |
| T0∞ | ↛ |
| PT0k, k ≥ 2 | thkk+1, x ⋀ (y → z) |
| PT0∞ | x ⋀ (y → z) |
| T1k, k ≥ 2 | th2k+1, → |
| T1∞ | → |
| PT1k, k ≥ 2 | th2k+1, x ⋁ (y + z) |
| PT1∞ | x ⋁ (y + z) |
| M | ⋀, ⋁, 0, 1 |
| MP0 | ⋀, ⋁, 0 |
| MP1 | ⋀, ⋁, 1 |
| MP | ⋀, ⋁ |
| MT0k, k ≥ 2 | thkk+1, 0 |
| MT0∞ | x ⋀ (y ⋁ z), 0 |
| MPT0k, k ≥ 2 | thkk+1 for k ≥ 3, maj, x ⋀ (y ⋁ z) for k = 2 |
| MPT0∞ | x ⋀ (y ⋁ z) |
| MT1k, k ≥ 2 | th2k+1, 1 |
| MT1∞ | x ⋁ (y ⋀ z), 1 |
| MPT1k, k ≥ 2 | th2k+1 for k ≥ 3, maj, x ⋁ (y ⋀ z) for k = 2 |
| MPT1∞ | x ⋁ (y ⋀ z) |
| Λ | ⋀, 0, 1 |
| ΛP0 | ⋀, 0 |
| ΛP1 | ⋀, 1 |
| ΛP | ⋀ |
| V | ⋁, 0, 1 |
| VP0 | ⋁, 0 |
| VP1 | ⋁, 1 |
| VP | ⋁ |
| D | maj, ¬ |
| DP | maj, x + y + z |
| DM | maj |
| A | ↔, 0 |
| AD | ¬, x + y + z |
| AP0 | |
| AP1 | ↔ |
| AP | x + y + z |
| U | ¬, 0 |
| UD | ¬ |
| UM | 0, 1 |
| UP0 | 0 |
| UP1 | 1 |
| ⊥ |
The eight infinite families have actually also members with k = 1, but these appear separately in the table: , , , , , .
The lattice has a natural symmetry mapping each clone C to its dual clone }, where is the de Morgan dual of a Boolean function f. For example, , , and .
Applications
The complete classification of Boolean clones given by Post helps to resolve various questions about classes of Boolean functions. For example:- An inspection of the lattice shows that the maximal clones different from ⊤ (often called Post's classes) are M, D, A, P0, P1, and every proper subclone of ⊤ is contained in one of them. As a set B of connectives is functionally complete if and only if it generates ⊤, we obtain the following characterization: B is functionally complete iff it is not included in one of the five Post's classes.
- The satisfiability problem for Boolean formulas is NP-completeNP-completeIn computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
by Cook's theoremCook's theoremIn computational complexity theory, the Cook–Levin theorem, also known as Cook's theorem, states that the Boolean satisfiability problem is NP-complete...
. Consider a restricted version of the problem: for a fixed finite set B of connectives, let B-SAT be the algorithmic problem of checking whether a given B-formula is satisfiable. Lewis used the description of Post's lattice to show that B-SAT is NP-complete if the function ↛ can be generated from B (i.e.), and in all the other cases B-SAT is polynomial-timeP (complexity)In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
decidable.
Variants
Post originally did not work with the modern definition of clones, but with the so-called iterative systems, which are sets of operations closed under substitutionas well as permutation and identification of variables. The main difference is that iterative systems do not necessarily contain all projections. Every clone is an iterative system, and there are 20 non-empty iterative systems which are not clones. (Post also excluded the empty iterative system from the classification, hence his diagram has no least element and fails to be a lattice.) As another alternative, some authors work with the notion of a closed class, which is an iterative system closed under introduction of dummy variables. There are four closed classes which are not clones: the empty set, the set of constant 0 functions, the set of constant 1 functions, and the set of all constant functions.
Composition alone does not allow to generate a nullary function from the corresponding unary constant function, this is the technical reason why nullary functions are excluded from clones in Post's classification. If we lift the restriction, we get more clones. Namely, each clone C in Post's lattice which contains at least one constant function corresponds to two clones under the less restrictive definition: C, and C together with all nullary functions whose unary versions are in C.