
Preference (economics)
Encyclopedia
In economics
and other social sciences, preference refers to the set of assumptions related to ordering some alternatives, based on the degree of happiness
, satisfaction, gratification
, enjoyment, or utility
they provide, a process which results in an optimal "choice
" (whether real or imagined). Although economists are usually not interested in choices or preferences in themselves, they are interested in the theory of choice because it serves as a background for empirical demand analysis.
started to affect economics through the notion that any theoretical concept used in a theory should be related to observables. Whereas economists in the 18th and 19th centuries felt comfortable theorizing about utility, with the advent of logical positivism in the 20th century, they felt that it needed more of an empirical structure. Because binary choices
are directly observable, it instantly appealed economists. The search for observables in microeconomics is taken even further by revealed preference theory
.
Since the pioneer efforts of Frisch in the 1920s, one of the major issues which has pervaded the theory of preferences is the representability of a preference structure with a real-valued function. This has been achieved by mapping it to the mathematical index called utility. Gerard Debreu
, influenced by the ideas of the Bourbaki group, championed the axiomatization of consumer theory in the 1950s, and the tools he borrowed from the mathematical field of binary relations have become mainstream since then. Even though the economics of choice can be examined either at the level of utility functions or at the level of preferences, to move from one to the other can be useful. For example, shifting the conceptual basis from an abstract preference relation to an abstract utility scale results in a new mathematical framework, allowing new kinds of conditions on the structure of preference to be formulated and investigated.
Another historical turnpoint can be traced back to 1895, when Georg Cantor
, proved in a theorem that if a binary relation is linearly ordered, then it is also isomorphically embeddable in the ordered real numbers. This notion would become very influential for the theory of preferences in economics: by the 1940s prominent authors such as Paul Samuelson
, would theorize about people actually having weakly ordered preferences.
People rank or order their preferences in a consistent way, or, more formally, they do not violate the axiom of transitivity:
If alternative is preferred to alternative
is preferred to alternative  , and
, and  to
to  , then
, then  is preferred to
is preferred to  .
.
The language of binary relations allow one to write down exactly what is meant by "ranked set of preferences", and thus gives an unambiguous definition of order. A preference relation should not be confused with the order relation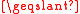 used to indicate which of two real numbers is larger. Order relations satisfy an extra condition:
used to indicate which of two real numbers is larger. Order relations satisfy an extra condition:
 , and
, and 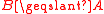 , implies
, implies 
which does not always holds in preference relations; hence, an indifference relation is used in its place (the symbol denotes this kind of relation).
denotes this kind of relation).
A system of preferences or preference structure refers to the set of qualitative relations between different alternatives of consumption. For example, if the alternatives are:
In this example, a preference structure would be:
"The apple is at least as preferred as the orange", and "The orange is as least as preferred as the Banana". One can use to symbolize that some alternative is "at least as preferred as" another one, which is just a binary relation on the set of alternatives. Therefore:
to symbolize that some alternative is "at least as preferred as" another one, which is just a binary relation on the set of alternatives. Therefore:
The former qualitative relation can be preserved when mapped into a numerical structure, if we impose certain desirable properties over the binary relation: these are the axioms of preference order. For instance: Let us take the apple and assign it the arbitrary number 5.Then take the orange and let us assign it a value lower than 5, since the orange is less preferred than the apple. If this procedure is extended to the banana, one may prove by induction that if is defined on {apple, orange} and it represents a well-defined binary relation called "at least as preferred as" on this set, then it can be extended to a function
is defined on {apple, orange} and it represents a well-defined binary relation called "at least as preferred as" on this set, then it can be extended to a function  defined on {apple, orange, banana} and it will represent "at least as preferred as" on this larger set.
defined on {apple, orange, banana} and it will represent "at least as preferred as" on this larger set.
Example:
5 > 3 > 2 = u(apple) > u(orange) > u(banana)
and this is consistent with Apple Orange, and with Orange
Orange, and with Orange  Banana.
Banana.
Since consumer theory often requires continuous utility functions, this additional axiom is imposed as well:
The continuity assumption is "too strong" in the sense that it indeed guarantees the existence of a continuous utility function representation. Although continuity of the preference relation is a sufficient condition, but it is not necessary.
Although some authors include reflexivity
as one of the axioms required to obtain representability (this axiom states that ), it is redundant inasmuch as the completeness axiom implies it already.
), it is redundant inasmuch as the completeness axiom implies it already.
Here is an illustrative example of the normative implications of the theory of preferences: Consider a decision maker who needs to make a choice. Assume that this is a choice of where to live or whom to marry and that the decision maker has asked an economist for advice. The economist, who wants to engage in normative science, attempts to tell the decision maker how she should make decisions.
Economist: I suggest that you attach a utility index to each alternative, and choose the alternative with the highest utility.
Decision Maker: You've been brainwashed. You think only in terms of functions. But this is an important decision, there are people involved, emotions, these are not functions!
Economist: Would you feel comfortable with cycling among three possible options? Preferrig x to y, and then y to z, but then again z to x?
Decision Maker: No, this is very silly and counterproductive. I told you that there are people involved, and I don't want to play with their feelings.
Economist: Good. So now let me tell you a secret: if you follow these two conditions -making decision, and avoid cycling, then you can be described as if you are maximizing a utility function.
Consumers whose preference structures violate transitivity
would get exposed to being milked by some unscrupulous person. For instance, Maria prefers apples to oranges, oranges to bananas, and bananas to apples. Let her be endowed with an apple, which she can trade in a market. Because she prefers bananas to apples, she is willing to pay, say, one cent to trade her apple for a banana. Afterwards, Maria is willing to pay another cent to trade her banana for an orange, and again the orange for an apple, and so on. There are other examples of this kind of "irrational" behaviour.
Completeness implies that some choice will be made, an assertion that is more philosophically questionable. In most applications, the set of consumption alternatives is infinite and the consumer is not conscious of all preferences. For example, one does not have to choose over going on holiday by plane or by train: if one does not have enough money to go on holiday anyway then it is not necessary to attach a preference order to those alternatives (although it can be nice to dream about what one would do if one would win the lottery). However, preference can be interpreted as a hypothetical choice that could be made rather than a conscious state of mind. In this case, completeness amounts to an assumption that the consumers can always make up their mind whether they are indifferent or prefer one option when presented with any pair of options.
Under some extreme circumstances there is no "rational" choice available. For instance, if asked to choose which one of one's children will be killed, as in Sophie's Choice
, there is no rational way out of it. In that case preferences would be incomplete, since "not being able to choose" is not the same as "being indifferent".
The indifference relation ~ is an equivalence relation
. Thus we have a quotient set S/~ of equivalence classes of S, which forms a partition
of S. Each equivalence class is a set of packages that is equally preferred.
If there are only two commodities, the equivalence classes can be graphically represented as indifference curve
s.
Based on the preference relation on S we have a preference relation on S/~. As opposed to the former, the latter is antisymmetric
and a total order
.
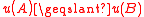 if and only if
if and only if
 . When a preference order is both transitive and complete, then it is standard practice to call it a rational preference relation, and the people who comply with it are rational agents. A transitive and complete relation is called a weak order (or total preorder). The literature on preferences is far from being standardized regarding terms such as complete, partial, strong, and weak. Together with the terms "total", "linear", "strong complete", "quasi-orders", "pre-orders" and "sub-orders", which also have a different meaning depending on the author's taste, there has been an abuse of semantics in the literature.
. When a preference order is both transitive and complete, then it is standard practice to call it a rational preference relation, and the people who comply with it are rational agents. A transitive and complete relation is called a weak order (or total preorder). The literature on preferences is far from being standardized regarding terms such as complete, partial, strong, and weak. Together with the terms "total", "linear", "strong complete", "quasi-orders", "pre-orders" and "sub-orders", which also have a different meaning depending on the author's taste, there has been an abuse of semantics in the literature.
A continuous
utility function always exists if is a continuous rational preference relation on
is a continuous rational preference relation on 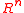 . For any such preference relation, there are many continuous utility functions that represent it. Conversely, every utility function can be used to construct a unique preference relation.
. For any such preference relation, there are many continuous utility functions that represent it. Conversely, every utility function can be used to construct a unique preference relation.
All the above is independent of the prices of the goods and services and of the budget constraints faced by consumers. These determine the feasible bundles (which they can afford). According to the standard theory, consumers chooses a bundle within their budget such that no other feasible bundle is preferred over it; therefore their utility is maximized.
 from the weaker one
from the weaker one  , and viceversa, suggest in principle an alternative approach of starting with the strict relation
, and viceversa, suggest in principle an alternative approach of starting with the strict relation  as the primitive concept and deriving the weaker one and the indifference relation. However, an indifference relation derived this way will generally not be transitive.
as the primitive concept and deriving the weaker one and the indifference relation. However, an indifference relation derived this way will generally not be transitive.
states that voting systems sometimes can not convert individual preferences into desirable community-wide acts of choice.
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
and other social sciences, preference refers to the set of assumptions related to ordering some alternatives, based on the degree of happiness
Happiness
Happiness is a mental state of well-being characterized by positive emotions ranging from contentment to intense joy. A variety of biological, psychological, religious, and philosophical approaches have striven to define happiness and identify its sources....
, satisfaction, gratification
Gratification
Gratification is the pleasurable emotional reaction of happiness in response to a fulfillment of a desire or goal.Gratification, like all emotions, is a motivator of behavior and thus plays a role in the entire range of human social systems....
, enjoyment, or utility
Utility
In economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service....
they provide, a process which results in an optimal "choice
Choice
Choice consists of the mental process of judging the merits of multiple options and selecting one of them. While a choice can be made between imagined options , often a choice is made between real options, and followed by the corresponding action...
" (whether real or imagined). Although economists are usually not interested in choices or preferences in themselves, they are interested in the theory of choice because it serves as a background for empirical demand analysis.
History
Ragnar Frisch gave the first rigorous axiomatic introduction of a preference relation in 1926. Up to then, economists had developed an elaborated theory of demand without the need to resort on any primitive characteristics of people. This changed at the end of the 19th and the beginning of the 20th century, when logical positivismLogical positivism
Logical positivism is a philosophy that combines empiricism—the idea that observational evidence is indispensable for knowledge—with a version of rationalism incorporating mathematical and logico-linguistic constructs and deductions of epistemology.It may be considered as a type of analytic...
started to affect economics through the notion that any theoretical concept used in a theory should be related to observables. Whereas economists in the 18th and 19th centuries felt comfortable theorizing about utility, with the advent of logical positivism in the 20th century, they felt that it needed more of an empirical structure. Because binary choices
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
are directly observable, it instantly appealed economists. The search for observables in microeconomics is taken even further by revealed preference theory
Revealed preference
Revealed preference theory, pioneered by American economist Paul Samuelson, is a method by which it is possible to discern the best possible option on the basis of consumer behavior. Essentially, this means that the preferences of consumers can be revealed by their purchasing habits...
.
Since the pioneer efforts of Frisch in the 1920s, one of the major issues which has pervaded the theory of preferences is the representability of a preference structure with a real-valued function. This has been achieved by mapping it to the mathematical index called utility. Gerard Debreu
Gerard Debreu
Gérard Debreu was a French economist and mathematician, who also came to have United States citizenship. Best known as a professor of economics at the University of California, Berkeley, where he began work in 1962, he won the 1983 Nobel Memorial Prize in Economics.-Biography:His father was the...
, influenced by the ideas of the Bourbaki group, championed the axiomatization of consumer theory in the 1950s, and the tools he borrowed from the mathematical field of binary relations have become mainstream since then. Even though the economics of choice can be examined either at the level of utility functions or at the level of preferences, to move from one to the other can be useful. For example, shifting the conceptual basis from an abstract preference relation to an abstract utility scale results in a new mathematical framework, allowing new kinds of conditions on the structure of preference to be formulated and investigated.
Another historical turnpoint can be traced back to 1895, when Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
, proved in a theorem that if a binary relation is linearly ordered, then it is also isomorphically embeddable in the ordered real numbers. This notion would become very influential for the theory of preferences in economics: by the 1940s prominent authors such as Paul Samuelson
Paul Samuelson
Paul Anthony Samuelson was an American economist, and the first American to win the Nobel Memorial Prize in Economic Sciences. The Swedish Royal Academies stated, when awarding the prize, that he "has done more than any other contemporary economist to raise the level of scientific analysis in...
, would theorize about people actually having weakly ordered preferences.
Basic premises
In economics people face a set of possible consumption bundles. Of all the available bundles of goods and services, only one is ultimately chosen. The theory of preferences seeks an analytical solution to the problem of getting to this ultimate choice (the optimal choice) using a system of preferences within a budgetary limitation. Choice is an act, whereas preferences are a state of mind.People rank or order their preferences in a consistent way, or, more formally, they do not violate the axiom of transitivity:
If alternative
 is preferred to alternative
is preferred to alternative  , and
, and  to
to  , then
, then  is preferred to
is preferred to  .
.The language of binary relations allow one to write down exactly what is meant by "ranked set of preferences", and thus gives an unambiguous definition of order. A preference relation should not be confused with the order relation
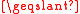 used to indicate which of two real numbers is larger. Order relations satisfy an extra condition:
used to indicate which of two real numbers is larger. Order relations satisfy an extra condition: , and
, and 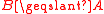 , implies
, implies 
which does not always holds in preference relations; hence, an indifference relation is used in its place (the symbol
 denotes this kind of relation).
denotes this kind of relation).A system of preferences or preference structure refers to the set of qualitative relations between different alternatives of consumption. For example, if the alternatives are:
- Apple
- Orange
- Banana
In this example, a preference structure would be:
"The apple is at least as preferred as the orange", and "The orange is as least as preferred as the Banana". One can use
 to symbolize that some alternative is "at least as preferred as" another one, which is just a binary relation on the set of alternatives. Therefore:
to symbolize that some alternative is "at least as preferred as" another one, which is just a binary relation on the set of alternatives. Therefore:- Apple
 Orange
Orange - Orange
 Banana
Banana
The former qualitative relation can be preserved when mapped into a numerical structure, if we impose certain desirable properties over the binary relation: these are the axioms of preference order. For instance: Let us take the apple and assign it the arbitrary number 5.Then take the orange and let us assign it a value lower than 5, since the orange is less preferred than the apple. If this procedure is extended to the banana, one may prove by induction that if
 is defined on {apple, orange} and it represents a well-defined binary relation called "at least as preferred as" on this set, then it can be extended to a function
is defined on {apple, orange} and it represents a well-defined binary relation called "at least as preferred as" on this set, then it can be extended to a function  defined on {apple, orange, banana} and it will represent "at least as preferred as" on this larger set.
defined on {apple, orange, banana} and it will represent "at least as preferred as" on this larger set.Example:
- Apple = 5
- Orange = 3
- Banana = 2
5 > 3 > 2 = u(apple) > u(orange) > u(banana)
and this is consistent with Apple
 Orange, and with Orange
Orange, and with Orange  Banana.
Banana.Axioms of order
- CompletenessTotal relationIn mathematics, a binary relation R over a set X is total if for all a and b in X, a is related to b or b is related to a .In mathematical notation, this is\forall a, b \in X,\ a R b \or b R a....
: for all and
and  we have
we have  or
or  or both.
or both.
Since consumer theory often requires continuous utility functions, this additional axiom is imposed as well:
- Continuity: If
 , then all the points that are very close to
, then all the points that are very close to  are also strictly better than
are also strictly better than  , and vice versa, all the points that are very close to
, and vice versa, all the points that are very close to  are also strictly worse than
are also strictly worse than  . More formally: let X be endowed with a topology. A preference relation
. More formally: let X be endowed with a topology. A preference relation  is continuous if
is continuous if 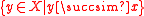 and
and  are closed for all
are closed for all 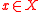
The continuity assumption is "too strong" in the sense that it indeed guarantees the existence of a continuous utility function representation. Although continuity of the preference relation is a sufficient condition, but it is not necessary.
Although some authors include reflexivity
Reflexive relation
In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...
as one of the axioms required to obtain representability (this axiom states that
 ), it is redundant inasmuch as the completeness axiom implies it already.
), it is redundant inasmuch as the completeness axiom implies it already.Most commonly used axioms
- Order-theoretic: acyclicity, transitivity, the semiorder property, completeness
- Topological: continuity, openness or closedness of the preference sets
- Linear-space: convexityConvex preferencesIn economics, convex preferences refer to a property of an individual's ordering of various outcomes which roughly corresponds to the idea that "averages are better than the extremes"...
, homogeneity, translation-invariance
Normative interpretations of the axioms
Everyday experience suggest that people at least talk about their preferences as if they had personal "standards of judgment" capable of being applied to the particular domain of alternatives that present themselves from time to time. Thus, the axioms are an attempt to model the decision maker's preferences, not over the actual choice, but over the type of desirable procedure (a procedure that any human being would like to follow). Behavioral economics investigates inconsistent behavior (i.e. behavior that violates the axioms) of people. Believing in axioms in a normative way does not imply that it is mandatory to behave according to them. Instead, they are a mode of behavior suggested; its what people would like to see themselves following.Here is an illustrative example of the normative implications of the theory of preferences: Consider a decision maker who needs to make a choice. Assume that this is a choice of where to live or whom to marry and that the decision maker has asked an economist for advice. The economist, who wants to engage in normative science, attempts to tell the decision maker how she should make decisions.
Economist: I suggest that you attach a utility index to each alternative, and choose the alternative with the highest utility.
Decision Maker: You've been brainwashed. You think only in terms of functions. But this is an important decision, there are people involved, emotions, these are not functions!
Economist: Would you feel comfortable with cycling among three possible options? Preferrig x to y, and then y to z, but then again z to x?
Decision Maker: No, this is very silly and counterproductive. I told you that there are people involved, and I don't want to play with their feelings.
Economist: Good. So now let me tell you a secret: if you follow these two conditions -making decision, and avoid cycling, then you can be described as if you are maximizing a utility function.
Consumers whose preference structures violate transitivity
Voting paradox
The voting paradox is a situation noted by the Marquis de Condorcet in the late 18th century, in which collective preferences can be cyclic , even if the preferences of individual voters are not. This is paradoxical, because it means that majority wishes can be in conflict with each other...
would get exposed to being milked by some unscrupulous person. For instance, Maria prefers apples to oranges, oranges to bananas, and bananas to apples. Let her be endowed with an apple, which she can trade in a market. Because she prefers bananas to apples, she is willing to pay, say, one cent to trade her apple for a banana. Afterwards, Maria is willing to pay another cent to trade her banana for an orange, and again the orange for an apple, and so on. There are other examples of this kind of "irrational" behaviour.
Completeness implies that some choice will be made, an assertion that is more philosophically questionable. In most applications, the set of consumption alternatives is infinite and the consumer is not conscious of all preferences. For example, one does not have to choose over going on holiday by plane or by train: if one does not have enough money to go on holiday anyway then it is not necessary to attach a preference order to those alternatives (although it can be nice to dream about what one would do if one would win the lottery). However, preference can be interpreted as a hypothetical choice that could be made rather than a conscious state of mind. In this case, completeness amounts to an assumption that the consumers can always make up their mind whether they are indifferent or prefer one option when presented with any pair of options.
Under some extreme circumstances there is no "rational" choice available. For instance, if asked to choose which one of one's children will be killed, as in Sophie's Choice
Sophie's Choice (novel)
Sophie's Choice is a novel by William Styron published in 1979. It concerns a young American Southerner, an aspiring writer, who befriends the Jewish Nathan Landau and his beautiful lover Sophie, a Polish survivor of the Nazi concentration camps...
, there is no rational way out of it. In that case preferences would be incomplete, since "not being able to choose" is not the same as "being indifferent".
The indifference relation ~ is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
. Thus we have a quotient set S/~ of equivalence classes of S, which forms a partition
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...
of S. Each equivalence class is a set of packages that is equally preferred.
If there are only two commodities, the equivalence classes can be graphically represented as indifference curve
Indifference curve
In microeconomic theory, an indifference curve is a graph showing different bundles of goods between which a consumer is indifferent. That is, at each point on the curve, the consumer has no preference for one bundle over another. One can equivalently refer to each point on the indifference curve...
s.
Based on the preference relation on S we have a preference relation on S/~. As opposed to the former, the latter is antisymmetric
Antisymmetric relation
In mathematics, a binary relation R on a set X is antisymmetric if, for all a and b in Xor, equivalently,In mathematical notation, this is:\forall a, b \in X,\ R \and R \; \Rightarrow \; a = bor, equivalently,...
and a total order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
.
Applications to theories of utility
In economics, a utility function is often used to represent a preference structure such that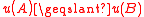 if and only if
if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
 . When a preference order is both transitive and complete, then it is standard practice to call it a rational preference relation, and the people who comply with it are rational agents. A transitive and complete relation is called a weak order (or total preorder). The literature on preferences is far from being standardized regarding terms such as complete, partial, strong, and weak. Together with the terms "total", "linear", "strong complete", "quasi-orders", "pre-orders" and "sub-orders", which also have a different meaning depending on the author's taste, there has been an abuse of semantics in the literature.
. When a preference order is both transitive and complete, then it is standard practice to call it a rational preference relation, and the people who comply with it are rational agents. A transitive and complete relation is called a weak order (or total preorder). The literature on preferences is far from being standardized regarding terms such as complete, partial, strong, and weak. Together with the terms "total", "linear", "strong complete", "quasi-orders", "pre-orders" and "sub-orders", which also have a different meaning depending on the author's taste, there has been an abuse of semantics in the literature.A continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
utility function always exists if
 is a continuous rational preference relation on
is a continuous rational preference relation on 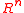 . For any such preference relation, there are many continuous utility functions that represent it. Conversely, every utility function can be used to construct a unique preference relation.
. For any such preference relation, there are many continuous utility functions that represent it. Conversely, every utility function can be used to construct a unique preference relation.All the above is independent of the prices of the goods and services and of the budget constraints faced by consumers. These determine the feasible bundles (which they can afford). According to the standard theory, consumers chooses a bundle within their budget such that no other feasible bundle is preferred over it; therefore their utility is maximized.
Primitive equivalents of some known properties of utility functions
- An increasing utility function is associated with a monotonic preference relation.
- A utility function that is non-constant in the neighborhood of x is associated with a locally non-satiated preference order.
- Quasi-concave utility functions are associated with a convex preference order. When non-convex preferences arise, the Shapley–Folkman lemmaShapley–Folkman lemmaIn geometry and economics, the Shapley–Folkman lemma describes the Minkowski addition of sets in a vector space. Minkowski addition is defined as the addition of the sets' members: for example, adding the set consisting of the integers zero and one to itself yields the set consisting of...
is applicable. - Weakly separable utility functions are associated with the weak separability of preferences.
Strict versus weak
The possibility of defining a strict preference relation from the weaker one
from the weaker one  , and viceversa, suggest in principle an alternative approach of starting with the strict relation
, and viceversa, suggest in principle an alternative approach of starting with the strict relation  as the primitive concept and deriving the weaker one and the indifference relation. However, an indifference relation derived this way will generally not be transitive.
as the primitive concept and deriving the weaker one and the indifference relation. However, an indifference relation derived this way will generally not be transitive.Agreggation
Under certain assumptions, individual preferences can be aggregated onto the preferences of a group of people. As a result of agreggation, Arrow's impossibility theoremArrow's impossibility theorem
In social choice theory, Arrow’s impossibility theorem, the General Possibility Theorem, or Arrow’s paradox, states that, when voters have three or more distinct alternatives , no voting system can convert the ranked preferences of individuals into a community-wide ranking while also meeting a...
states that voting systems sometimes can not convert individual preferences into desirable community-wide acts of choice.
See also
- Arrow's paradox
- Behavioral economics
- Convex preferencesConvex preferencesIn economics, convex preferences refer to a property of an individual's ordering of various outcomes which roughly corresponds to the idea that "averages are better than the extremes"...
- Economic subjectivism
- Gibbard-Satterthwaite theoremGibbard-Satterthwaite theoremThe Gibbard–Satterthwaite theorem, named after Allan Gibbard and Mark Satterthwaite, is a result about the deterministic voting systems that choose a single winner using only the preferences of the voters, where each voter ranks all candidates in order of preference...
- Lexicographic preferencesLexicographic preferencesLexicographic preferences describe comparative preferences where an economic agent infinitely prefers one good to another . Thus if offered several bundles of goods, the agent will choose the bundle that offers the most X, no matter how much Y there is...
- Pairwise comparisonPairwise comparisonPairwise comparison generally refers to any process of comparing entities in pairs to judge which of each entity is preferred, or has a greater amount of some quantitative property. The method of pairwise comparison is used in the scientific study of preferences, attitudes, voting systems, social...
- Preference regression (in marketing)Preference regression (in marketing)Preference regression is a statistical technique used by marketers to determine consumers’ preferred core benefits. It usually supplements product positioning techniques like multi dimensional scaling or factor analysis and is used to create ideal vectors on perceptual maps.-Application:Starting...
- Preferential votingPreferential votingPreferential voting is a type of ballot structure used in several electoral systems in which voters rank candidates in order of relative preference. For example, the voter may select their first choice as '1', their second preference a '2', and so on...
- Preferred numberPreferred numberIn industrial design, preferred numbers are standard guidelines for choosing exact product dimensions within a given set of constraints....
- Revealed preferenceRevealed preferenceRevealed preference theory, pioneered by American economist Paul Samuelson, is a method by which it is possible to discern the best possible option on the basis of consumer behavior. Essentially, this means that the preferences of consumers can be revealed by their purchasing habits...
- Second-order desire
- Strict weak orderingStrict weak orderingIn mathematics, especially order theory, a strict weak ordering is a binary relation In mathematics, especially order theory, a strict weak ordering is a binary relation ...
- Time preference theory of interest

