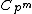Primary cyclic group
Encyclopedia
In mathematics
, a primary cyclic group is a group
that is both a cyclic group
and a p-primary group for some prime number
p.
That is, it has the form
for some prime number p, and natural number
m.
Every finite abelian group
G may be written as a finite direct sum of primary cyclic groups:

This expression is essentially unique: there is a bijection between the sets of groups in two such expressions, which maps each group to one that is isomorphic.
Primary cyclic groups are characterised among finitely generated abelian group
s as the torsion groups that cannot be expressed as a direct sum of two non-trivial groups. As such they, along with the group of integer
s, form the building blocks of finitely generated abelian groups.
The subgroups of a primary cyclic group are linearly ordered by inclusion. The only other groups that have this property are the quasicyclic groups.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a primary cyclic group is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
that is both a cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
and a p-primary group for some prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
p.
That is, it has the form
for some prime number p, and natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
m.
Every finite abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
G may be written as a finite direct sum of primary cyclic groups:

This expression is essentially unique: there is a bijection between the sets of groups in two such expressions, which maps each group to one that is isomorphic.
Primary cyclic groups are characterised among finitely generated abelian group
Finitely generated abelian group
In abstract algebra, an abelian group is called finitely generated if there exist finitely many elements x1,...,xs in G such that every x in G can be written in the formwith integers n1,...,ns...
s as the torsion groups that cannot be expressed as a direct sum of two non-trivial groups. As such they, along with the group of integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, form the building blocks of finitely generated abelian groups.
The subgroups of a primary cyclic group are linearly ordered by inclusion. The only other groups that have this property are the quasicyclic groups.