In mathematics

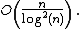
Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

 a primitive abundant number is an abundant number whose proper divisors are all deficient number

Deficient number

In number theory, a deficient number or defective number is a number n for which the sum of divisors σIn number theory, a deficient number or defective number is a number n for which the sum of divisors σIn number theory, a deficient number or defective number is a number n for which...

s.

For example, 20 is a primitive abundant number because:

1. The sum of its proper divisors is 1 + 2 + 4 + 5 + 10 = 22, so 20 is an abundant number.
2. The sums of the proper divisors of 1, 2, 4, 5 and 10 are 0, 1, 3, 1 and 8 respectively, so each of these numbers is a deficient number.

The first few primitive abundant numbers are:

20

20 (number)

20 is the natural number following 19 and preceding 21. A group of twenty units may also be referred to as a score.-In mathematics:*20 is the basis for vigesimal number systems....

, 70

70 (number)

70 is the natural number following 69 and preceding 71.-In mathematics:Its factorization makes it a sphenic number. 70 is a Pell number and a generalized heptagonal number, one of only two numbers to be both. Also, it is the seventh pentagonal number and the fourth 13-gonal number, as well as the...

, 88

88 (number)

88 is the natural number following 87 and preceding 89.- In mathematics :Eighty-Eight is a refactorable number, a primitive semiperfect number and an untouchable number...

, 104

104 (number)

104 is the natural number following 103 and preceding 105.- In mathematics :One hundred [and] four is a primitive semiperfect number and a composite number, with its divisors being 1, 2, 4, 8, 13, 26, 52 and 104. As it has 8 divisors total, and 8 is one of those divisors, 104 is a refactorable...

, 272, 304, 368, 464, 550, 572 ...

The smallest odd primitive abundant number is 945.

Properties

Every multiple of a primitive abundant number is an abundant number.

Every abundant number is a multiple of a primitive abundant number or a multiple of a perfect number.

There are an infinite number of primitive abundant numbers.

The number of primitive abundant numbers less than or equal to n is