Principle of covariance
Encyclopedia
In physics, the principle of covariance emphasizes formulation of physical laws using only those physical quantities the measurements of which the observers in different frames of reference
could unambiguously correlate.
Mathematically, the physical quantities must transform covariantly, that is, under a certain representation of the group
of coordinate transformations between admissible frames of reference of the physical theory. This group is referred to as the covariance group
.
Principle of covariance does not require invariance of the physical laws under the group of admissible transformations although in most cases the equations are actually invariant. However, in the theory of weak interactions the equations are not invariant under reflections (but are, of course, still covariant).
. Time is then absolute and the transformations between admissible frames of references are Galilean transformations which (together with rotations, translations, and reflections) form the Galilean group. The covariant physical quantities are Euclidian
scalars, vectors, and tensors. An example of a covariant equation is Newton's second law,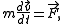
where the covariant quantities are the mass
of a moving body (scalar), the momentum 
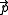of the body (vector), the force 
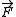acting on the body, and the invariant time 
.
the admissible frames of reference are all inertial frames. The transformations between frames are the Lorentz transformations which (together with the rotations, translations, and reflections) form the Poincaré group
. The convariant quantities are four-scalars, four-vectors etc., of the Minkowski space
(and also more complicated objects like bispinor
s and others). An example of a covariant equation is the Lorentz force
equation of motion of a charged particle in an electromagnetic field (a generalization of the second Newton's law)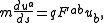
where
and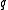 
are the mass and charge of the particle (invariant 4-scalars); 
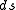is the invariant interval
(4-scalar);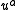
is the 4-velocity (4-vector); and 
is the electromagnetic field strength tensor
(4-tensor).
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
could unambiguously correlate.
Mathematically, the physical quantities must transform covariantly, that is, under a certain representation of the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of coordinate transformations between admissible frames of reference of the physical theory. This group is referred to as the covariance group
Covariance group
In physics, covariance group is a group of coordinate transformations between admissible frames of reference . The frames are assumed to provide equivalent description of physical phenomena...
.
Principle of covariance does not require invariance of the physical laws under the group of admissible transformations although in most cases the equations are actually invariant. However, in the theory of weak interactions the equations are not invariant under reflections (but are, of course, still covariant).
Covariance in Newtonian mechanics
In Newtonian mechanics the admissible frames of reference are inertial frames with relative velocities much smaller than the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
. Time is then absolute and the transformations between admissible frames of references are Galilean transformations which (together with rotations, translations, and reflections) form the Galilean group. The covariant physical quantities are Euclidian
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
scalars, vectors, and tensors. An example of a covariant equation is Newton's second law,
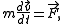
where the covariant quantities are the mass
of a moving body (scalar), the momentum 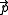of the body (vector), the force 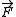acting on the body, and the invariant time .Covariance in special relativity
In special relativitySpecial relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
the admissible frames of reference are all inertial frames. The transformations between frames are the Lorentz transformations which (together with the rotations, translations, and reflections) form the Poincaré group
Poincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
. The convariant quantities are four-scalars, four-vectors etc., of the Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
(and also more complicated objects like bispinor
Bispinor
In physics, bispinor is a four-component object which transforms under the ⊕ representation of the covariance group of special relativity...
s and others). An example of a covariant equation is the Lorentz force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
equation of motion of a charged particle in an electromagnetic field (a generalization of the second Newton's law)
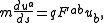
where
and 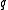are the mass and charge of the particle (invariant 4-scalars); 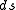is the invariant intervalInvariant interval
In physics, the invariant interval is the measure of separation between two arbitrarily close events in the spacetime of general or special theory of relativity. It is invariant under the coordinate transformations from the covariance group of the theory...
(4-scalar);
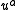is the 4-velocity (4-vector); and is the electromagnetic field strength tensorElectromagnetic tensor
The electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field of a physical system in Maxwell's theory of electromagnetism...
(4-tensor).