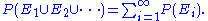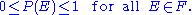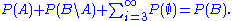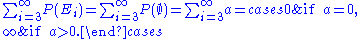Probability axioms
Encyclopedia
In probability theory
, the probability
P of some event
E, denoted , is usually defined in such a way that P satisfies the Kolmogorov axioms, named after Andrey Kolmogorov
, is usually defined in such a way that P satisfies the Kolmogorov axioms, named after Andrey Kolmogorov
, which are described below.
These assumptions can be summarised as: Let (Ω, F, P) be a measure space with P(Ω)=1. Then (Ω, F, P) is a probability space
, with sample space Ω, event space F and probability measure P.
An alternative approach to formalising probability, favoured by some Bayesians, is given by Cox's theorem
.
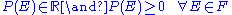
where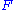 is the event space and
is the event space and  is any event in
is any event in 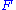 . In particular,
. In particular, 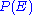 is always finite, in contrast with more general measure theory.
is always finite, in contrast with more general measure theory.
Symbols:
P(E)∈ℝ∧P(E)≥0 ∀E∈F
in the entire sample space will occur is 1. More specifically, there are no elementary events outside the sample space.
This is often overlooked in some mistaken probability calculations; if you cannot precisely define the whole sample space, then the probability of any subset cannot be defined either.
Some authors consider merely finitely additive probability spaces, in which case one just needs an algebra of sets
, rather than a σ-algebra.
and its interaction with the remaining two axioms. When studying axiomatic
probability theory
, many deep consequences follow from merely these three axioms.
In order to verify the monotonicity property, we set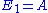 and
and 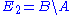 ,
,
where for
for 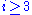 . It is easy to see that the sets
. It is easy to see that the sets 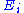
are pairwise disjoint and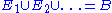 . Hence,
. Hence,
we obtain from the third axiom that
Since the left-hand side of this equation is a series of non-negative numbers, and that it converges to
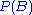 which is finite, we obtain both
which is finite, we obtain both 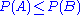 and
and 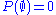 .
.
The second part of the statement is seen by contradiction: if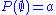 then the left hand side is not less than
then the left hand side is not less than
If then we obtain a contradiction, because the sum does not exceed
then we obtain a contradiction, because the sum does not exceed 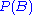 which is finite. Thus,
which is finite. Thus,  . We have shown as a byproduct of the proof of monotonicity that
. We have shown as a byproduct of the proof of monotonicity that 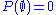 .
.
This is called the addition law of probability, or the sum rule.
That is, the probability that A or B will happen is the sum of the
probabilities that A will happen and that B will happen, minus the
probability that both A and B will happen. This can be extended to the inclusion-exclusion principle
.
That is, the probability that any event will not happen is 1 minus the probability that it will.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, the probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
P of some event
Event (probability theory)
In probability theory, an event is a set of outcomes to which a probability is assigned. Typically, when the sample space is finite, any subset of the sample space is an event...
E, denoted
 , is usually defined in such a way that P satisfies the Kolmogorov axioms, named after Andrey Kolmogorov
, is usually defined in such a way that P satisfies the Kolmogorov axioms, named after Andrey KolmogorovAndrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
, which are described below.
These assumptions can be summarised as: Let (Ω, F, P) be a measure space with P(Ω)=1. Then (Ω, F, P) is a probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
, with sample space Ω, event space F and probability measure P.
An alternative approach to formalising probability, favoured by some Bayesians, is given by Cox's theorem
Cox's theorem
Cox's theorem, named after the physicist Richard Threlkeld Cox, is a derivation of the laws of probability theory from a certain set of postulates. This derivation justifies the so-called "logical" interpretation of probability. As the laws of probability derived by Cox's theorem are applicable to...
.
First axiom
The probability of an event is a non-negative real number: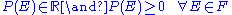
where
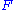 is the event space and
is the event space and  is any event in
is any event in 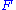 . In particular,
. In particular, 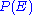 is always finite, in contrast with more general measure theory.
is always finite, in contrast with more general measure theory.Symbols:
P(E)∈ℝ∧P(E)≥0 ∀E∈F
Second axiom
This is the assumption of unit measure: that the probability that some elementary eventElementary event
In probability theory, an elementary event or atomic event is a singleton of a sample space. An outcome is an element of a sample space. An elementary event is a set containing exactly one outcome, not the outcome itself...
in the entire sample space will occur is 1. More specifically, there are no elementary events outside the sample space.
-
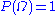 .
.
This is often overlooked in some mistaken probability calculations; if you cannot precisely define the whole sample space, then the probability of any subset cannot be defined either.
Third axiom
This is the assumption of σ-additivity:- Any countable sequence of pairwise disjoint (synonymous with mutually exclusive) events
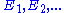 satisfies
satisfies
Some authors consider merely finitely additive probability spaces, in which case one just needs an algebra of sets
Algebra of sets
The algebra of sets develops and describes the basic properties and laws of sets, the set-theoretic operations of union, intersection, and complementation and the relations of set equality and set inclusion...
, rather than a σ-algebra.
Consequences
From the Kolmogorov axioms, one can deduce other useful rules for calculating probabilities.The numeric bound
It immediately follows from the monotonicity property thatProofs
The proofs of these properties are both interesting and insightful. They illustrate the power of the third axiom,and its interaction with the remaining two axioms. When studying axiomatic
Axiomatic
* In mathematics, an "axiomatic" theory is one based on axioms* Axiomatic , a collection of short stories by Greg Egan* Axiomatic , a 2005 album by Australian band Taxiride...
probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, many deep consequences follow from merely these three axioms.
In order to verify the monotonicity property, we set
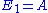 and
and 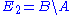 ,
,where
 for
for 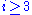 . It is easy to see that the sets
. It is easy to see that the sets 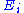
are pairwise disjoint and
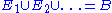 . Hence,
. Hence,we obtain from the third axiom that
Since the left-hand side of this equation is a series of non-negative numbers, and that it converges to
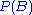 which is finite, we obtain both
which is finite, we obtain both 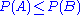 and
and 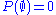 .
.The second part of the statement is seen by contradiction: if
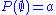 then the left hand side is not less than
then the left hand side is not less thanIf
 then we obtain a contradiction, because the sum does not exceed
then we obtain a contradiction, because the sum does not exceed 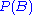 which is finite. Thus,
which is finite. Thus,  . We have shown as a byproduct of the proof of monotonicity that
. We have shown as a byproduct of the proof of monotonicity that 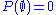 .
.More consequences
Another important property is:This is called the addition law of probability, or the sum rule.
That is, the probability that A or B will happen is the sum of the
probabilities that A will happen and that B will happen, minus the
probability that both A and B will happen. This can be extended to the inclusion-exclusion principle
Inclusion-exclusion principle
In combinatorics, the inclusion–exclusion principle is an equation relating the sizes of two sets and their union...
.
That is, the probability that any event will not happen is 1 minus the probability that it will.
See also
- Cox's theoremCox's theoremCox's theorem, named after the physicist Richard Threlkeld Cox, is a derivation of the laws of probability theory from a certain set of postulates. This derivation justifies the so-called "logical" interpretation of probability. As the laws of probability derived by Cox's theorem are applicable to...
- Law of total probabilityLaw of total probabilityIn probability theory, the law of total probability is a fundamental rule relating marginal probabilities to conditional probabilities.-Statement:The law of total probability is the proposition that if \left\...
- Measure Theory
- Borel AlgebraBorel algebraIn mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
- σ-AlgebraSigma-algebraIn mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
- Probability theoryProbability theoryProbability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
- Set theorySet theorySet theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
- Conditional probabilityConditional probabilityIn probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
Further reading
- Von Plato, Jan, 2005, "Grundbegriffe der Wahrscheinlichkeitsrechnung" in Grattan-Guinness, I.Ivor Grattan-GuinnessIvor Grattan-Guinness, born 23 June 1941, in Bakewell, in England, is a historian of mathematics and logic.He gained his Bachelor degree as a Mathematics Scholar at Wadham College, Oxford, got an M.Sc in Mathematical Logic and the Philosophy of Science at the London School of Economics in 1966...
, ed., Landmark Writings in Western Mathematics. Elsevier: 960-69. (in English)
External links
- The Legacy of Andrei Nikolaevich Kolmogorov Curriculum Vitae and Biography. Kolmogorov School. Ph.D. students and descendants of A.N. Kolmogorov. A.N. Kolmogorov works, books, papers, articles. Photographs and Portraits of A.N. Kolmogorov.