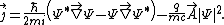Probability current
Encyclopedia
In quantum mechanics
, the probability current (sometimes called probability flux) is a mathematical quantity describing the flow of probability
density. Intuitively; if one pictures the probability density as an inhomogeneous fluid, then the probability current is the rate of flow of this fluid (change in probability per unit time
). This is analogous to hydrodynamic mass currents and electromagnetic
charge
currents. It is a vector
quantity
, but is complex-valued
. Therefore it is not a physical property that can be measured like mass density or electric current - the notion of a probability current is a theoretical abstraction, useful in some of the formalism in quantum mechanics.
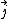of the wave function 
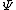in one dimension is defined as
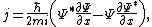
in three dimensions, this generalizes to
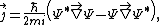
where:
These definitions utilize the position basis (i.e. for a wavefunction in position space, momentum space is possible). The 3-d form in terms of the real and imaginary parts
are:
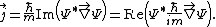
to be derived - in exactly the same forms as hydrodynamics and electromagnetism
:
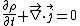
where the probability density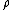
is defined as
.
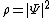If one were to integrate both sides of the continuity equation with respect to volume, so that
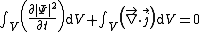
then the divergence theorem
implies the continuity equation is equivalent to the integral equation
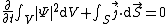
where the V is any volume and S is the boundary of V. This is the conservation law for probability in quantum mechanics.
In particular, if Ψ is a wavefunction describing a single particle, the integral in the first term of the preceding equation (without the time derivative) is the probability of obtaining a value within V when the position of the particle is measured. The second term is then the rate at which probability is flowing out of the volume V. Altogether the equation states that the time derivative of the change of the probability of the particle being measured in V is equal to the rate at which probability flows into V.
T and R can be defined by :
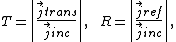
or equivalenetly:
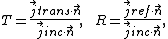
where jinc, jref and jtrans are the incident, reflected and transmitted probability currents respectively, and n is a unit vector normal
to the barrier. The vertical bars denote absolute value
s, here complex moduli, since the magnitudes of the current vectors are complex-valued.
Substituting these definitions into the first equation gives the intuitive relation, a statement of probability conservation:
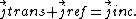
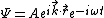
the associated probability current is
This is just the square of the amplitude of the wave times the particle's velocity,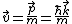
.
Note that the probability current is nonzero despite the fact that plane waves are stationary state
s and hence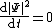
everywhere. This demonstrates that a particle may be in motion even if its spatial probability
density has no explicit time dependence.
of one spatial dimension and of length L
are, for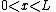
,
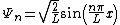
and zero elsewhere. The associated probability currents are
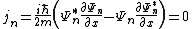
since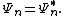
. For a charged particle the Hamiltonian operator is:
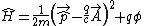
where:
The probability current now is similar to the previous, up to a correction term including the A-field:
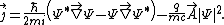
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the probability current (sometimes called probability flux) is a mathematical quantity describing the flow of probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
density. Intuitively; if one pictures the probability density as an inhomogeneous fluid, then the probability current is the rate of flow of this fluid (change in probability per unit time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
). This is analogous to hydrodynamic mass currents and electromagnetic
Electromagnetic
Electromagnetic may refer to:* Electromagnetism* Electromagnetic field* Electromagnetic force* Electromagnetic radiation* Electromagnetic induction* Electromagnetic spectrum...
charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
currents. It is a vector
Vector
Vector, a Latin word meaning "carrier", may refer in English to:-In computer science:*A one-dimensional array**Vector , a data type in the C++ Standard Template Library...
quantity
Quantity
Quantity is a property that can exist as a magnitude or multitude. Quantities can be compared in terms of "more" or "less" or "equal", or by assigning a numerical value in terms of a unit of measurement. Quantity is among the basic classes of things along with quality, substance, change, and relation...
, but is complex-valued
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
. Therefore it is not a physical property that can be measured like mass density or electric current - the notion of a probability current is a theoretical abstraction, useful in some of the formalism in quantum mechanics.
Definition (non-relativistic)
In non-relativistic quantum mechanics, the probability current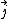 of the wave function 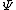in one dimension is defined as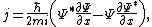 in three dimensions, this generalizes to
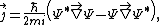
where:
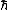is the reduced Planck constantPlanck constantThe Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
,- m is the reduced particle's massMassMass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
, - Ψ is the wavefunctionWavefunctionNot to be confused with the related concept of the Wave equationA wave function or wavefunction is a probability amplitude in quantum mechanics describing the quantum state of a particle and how it behaves. Typically, its values are complex numbers and, for a single particle, it is a function of...
, - denotes the delDelIn vector calculus, del is a vector differential operator, usually represented by the nabla symbol \nabla . When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus...
or gradientGradientIn vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
operator.
These definitions utilize the position basis (i.e. for a wavefunction in position space, momentum space is possible). The 3-d form in terms of the real and imaginary parts
Real and imaginary parts
In mathematics, a hypercomplex number has a real part and an imaginary part associated with it. This is most familiar in the context of complex numbers, but extends to the other hypercomplex algebras such as split-complex numbers and quaternions....
are:
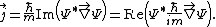
Continuity equation for quantum mechanics
The definition of probability current allows a continuity equationContinuity equation
A continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
to be derived - in exactly the same forms as hydrodynamics and electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
:
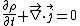
where the probability density
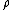is defined as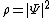.If one were to integrate both sides of the continuity equation with respect to volume, so that
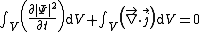
then the divergence theorem
Divergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
implies the continuity equation is equivalent to the integral equation
Integral equation
In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
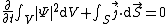
where the V is any volume and S is the boundary of V. This is the conservation law for probability in quantum mechanics.
In particular, if Ψ is a wavefunction describing a single particle, the integral in the first term of the preceding equation (without the time derivative) is the probability of obtaining a value within V when the position of the particle is measured. The second term is then the rate at which probability is flowing out of the volume V. Altogether the equation states that the time derivative of the change of the probability of the particle being measured in V is equal to the rate at which probability flows into V.
Transmission and reflection through potentials
In regions where a step potential or potential barrier occurs, the probability current is related to the transmission and reflection coefficients, respectively T and R; they measure the extent the particles reflect from the potential barrier or are transmitted through it. Both satisfy:T and R can be defined by :
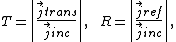
or equivalenetly:
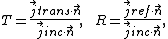
where jinc, jref and jtrans are the incident, reflected and transmitted probability currents respectively, and n is a unit vector normal
Surface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
to the barrier. The vertical bars denote absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
s, here complex moduli, since the magnitudes of the current vectors are complex-valued.
Substituting these definitions into the first equation gives the intuitive relation, a statement of probability conservation:
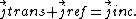
Plane wave
For the (three dimensional) plane wavePlane wave
In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....
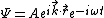
the associated probability current is
This is just the square of the amplitude of the wave times the particle's velocity,
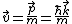.Note that the probability current is nonzero despite the fact that plane waves are stationary state
Stationary state
In quantum mechanics, a stationary state is an eigenvector of the Hamiltonian, implying the probability density associated with the wavefunction is independent of time . This corresponds to a quantum state with a single definite energy...
s and hence
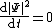
everywhere. This demonstrates that a particle may be in motion even if its spatial probability
density has no explicit time dependence.
Particle in a box
The energy eigenstates of a particle in a boxParticle in a box
In quantum mechanics, the particle in a box model describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems...
of one spatial dimension and of length L
are, for
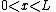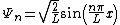
,and zero elsewhere. The associated probability currents are
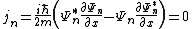
since
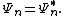
Definition (external electromagnetic field present)
The above definition should be modified for a system in an external electromagnetic fieldElectromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
. For a charged particle the Hamiltonian operator is:
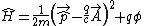
where:
-
is the 3-d momentum operatorMomentum operatorIn quantum mechanics, momentum is defined as an operator on the wave function. The Heisenberg uncertainty principle defines limits on how accurately the momentum and position of a single observable system can be known at once...
, - q is the electric chargeElectric chargeElectric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
of the particle. -
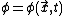is the scalar potentialScalar potentialA scalar potential is a fundamental concept in vector analysis and physics . The scalar potential is an example of a scalar field...
, in this case the electric potentialElectric potentialIn classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
, -
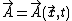is the vector potentialVector potentialIn vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
, here the magnetic potentialMagnetic potentialThe term magnetic potential can be used for either of two quantities in classical electromagnetism: the magnetic vector potential, A, and the magnetic scalar potential, ψ...
(aka "A-field"), -
is the kinetic momentumKinetic momentumIn physics, in particular electromagnetism, the kinetic momentum is a nonstandard term for the momentum of a charged particle due to its inertia. When a charged particle interacts with an electromagnetic field , there are two momenta: due to its inertia and due to the field...
of the particle,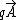
is the potential momentum of the particle, that is the momentum the particle gains due to the momentum stored in the A-field .
The probability current now is similar to the previous, up to a correction term including the A-field: