See Poker probability (Omaha)#Making hands based on rank type for the probabilities derived from these equations.

The probability

Probability

Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...

 derivations for starting hands making four of a kind, a full house, three of a kind, two pair, one pair and no pair in Omaha hold 'em

Omaha hold 'em

Omaha hold 'em is a community card poker game similar to Texas hold 'em, where each player is dealt four cards and must make his best hand using exactly two of them, plus exactly three of the five community cards...

 are separate for each of the starting hand rank types.

The derivations require identifying the individual cases that yield each possible hand and are sometimes rather detailed, so it is useful to use a notation to indicate the shape of the board for each case. The rank type of the hand is shown using upper case letters to indicate ranks. The ranks on the board are indicated using upper case letters for matches with the starting hand and lower case letters to indicate ranks that don't match the starting hand. So the rank type XXYZ is any hand with a pair of X with two additional ranks Y and Z and the board XYr represents a flop that contains one X, one of the non-paired ranks Y and one other rank r. Note that since Y and Z have an identical relationship to the starting hand—each represents an unpaired rank—XYr and XZr represent the same set of boards and are interchangeable, so derivations for this hand choose one of the two choices represented by Y. In addition to the upper and lower case letters, * is used to represent any rank not already represented on the board, and ? is used to represent any rank not already represented on the board and not included in the starting hand. So for the rank type XXYZ, the board XX* represents a flop that contains two Xs and any other rank (including Y and Z), but X?? is any flop that contains an X and any two cards of a rank other than X, Y or Z, and rrr?? is any board on the river that contains three cards of rank r and any two cards of ranks other than X, Y, Z or r.

Each table shows all of the boards that can make each hand and the derivation for the combination

Combination

In mathematics a combination is a way of selecting several things out of a larger group, where order does not matter. In smaller cases it is possible to count the number of combinations...

s for that board. Probabilities are determined by dividing the number of combinations for each hand by the 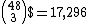boards on the flop, 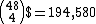boards on the turn, and 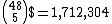boards at the river. The probabilities for the boards in each table total 1.0.

Derivations for starting hands with four of a kind

Starting hands with four of a kind (XXXX) can only improve to a full house or two pair. To make a full house, this hand needs to have two or three cards of the same rank appear on the board. To make two pair, another pair on the board is needed. Of course, any other hand holding a pair also makes at least a full house or two with either of these boards. The following table shows the derivations for making a full house, two pair or one pair when holding four of a kind.

Derivations for starting hands with three of a kind

To make a full house or three or four of a kind, starting hands with three of a kind (XXXY) need to either catch the case (last) X or catch two or three of the remaining Y cards (YY or YYY). They also improve to a full house if three or more of another rank appears on the board (rrr or rrrr), although any other hand holding a pair also makes a full house with this board. Three of a kind makes two pair if either a Y card or another pair appears on the board. The following tables show all the ways for XXXY to make four of a kind, a full house, three of a kind, two pair or one pair on the flop, turn and river.

Derivations for starting hands with two pair

Starting hands with two pair (XXYY) can improve to three of a kind, a full house or four of a kind when one or more of the four remaining X or Y cards appears (X, XX or XY). They also improve to a full house if three or more of another rank appears on the board (rrr or rrrr), although any other hand holding a pair also makes at least a full house with this board. If another pair appears the hand makes two pair, although any other hand holding a pair also makes at least two pair. The following tables show all the ways for XXYY to make four of a kind, a full house, three of a kind, two pair or one pair on the flop, turn and river.

Derivations for starting hands with one pair

Starting hands with one pair (XXYZ) can improve to three of a kind, a full house or four of a kind when either an X card is on the board or when two or three of the remaining Y or Z cards (YY or YYY) is on the board. They also improve to a full house if three or more of another rank is on the board (rrr or rrrr), although any other hand holding a pair also makes a full house with this board. These hands make two pair if another pair (rr) appears on the board. The following tables show all the ways for XXYZ to make four of a kind, a full house, three of a kind, two pair or one pair on the flop, turn and river.

Derivations for starting hands with no pair

Starting hands with no pair (XYZR) can improve when two or three of the remaining X, Y, Z or R cards (XX or XXX) appears on the board. These hands can make two pair or a full house when two of more ranks from the hand appear (XY or XXY). They also can make three of a kind or a pair if two or three other ranks (ss or sss) appear, although these boards are likely to improve other hands at least as much. The following tables show all the ways for XYZR to make four of a kind, a full house, three of a kind, two pair, one pair or no pair (high card) on the flop, turn and river.

See also

• Binomial coefficient
  Binomial coefficient
  In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...