
Procedural parameter
Encyclopedia
In computing
, a procedural parameter is a parameter
of a procedure
that is itself a procedure.
This concept is an extremely powerful and versatile programming tool, because it allows programmers to modify certain steps of a library procedure
in arbitrarily complicated ways, without having to understand or modify the code of that procedure.
This tool is particularly effective and convenient in languages that support local function definitions
, such as Pascal and the modern GNU dialect
of C. It is even more so when function closures
are available. The same functionality (and more) is provided by objects in object oriented programming language
s, but at a significantly higher cost.
procedure P(f):
return f(6,3) * f(2,1)
When calling the subroutine P, one must give it one argument, that must be some previously defined function compatible with the way P uses its parameter f. For example, if we define
procedure plus(x, y):
return x + y
then we may call P (plus), and the result will be plus(6,3) * plus(2,1) = (6 + 3)*(2 + 1) = 27. On the other hand, if we define
procedure quot(u, v):
return u/v
then the call P (quot) will return quot(6,3)*quot(2,1) = (6/3)*(2/1) = 4. Finally, if we define
procedure evil(z)
return z + 100
then the call P (evil) will not make much sense, and may be flagged as an error.
int P ( int f (int a, int b) )
{ return f(6,3) * f(2,1); }
In principle, the actual function actf that is passed as argument when P is called must be type-compatible with the declared type of the procedure parameter f. This usually means that actf and f must return the same type of result, must have the same number of arguments, and corresponding arguments must have the same type. The names of the arguments need not be the same, however, as shown by the plus and quot examples above. However, some programming languages may me more restrictive or more liberal in this regard.
The implementation of these scoping rules is not trivial. By the time that actf is finally executed, the activation records where its environment variables live may be arbitrarily deep in the stack. This is the so-called downwards funarg problem.
algorithm, that takes two integer parameters a,b and two procedural parameters prec, swap:
procedure isort(a, b, prec, swap):
integer i, j;
i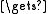 a;
a;
while i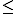 b do
b do
j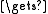 i
i
while j > a and prec(j, j−1) do
swap(j, j−1); j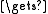 j−1
j−1
i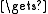 i+1
i+1
This procedure can be used to sort the elements x[a] through x[b] of some array x, of arbitrary type, in a user-specified order. The parameters prec and swap should be two functions, defined by the client, both taking two integers r, s between a and b. The prec function should return true if and only if the data stored in x[r] should precede the data stored in x[s], in the ordering defined by the client. The swap function should exchange the contents of x[r] and x[s], and return no result.
By the proper choice of the functions prec and swap, the same isort procedure can be used to reorder arrays of any data type, stored in any medium and organized in any data structure that provides indexed access to individual array elements. (Note however that there are sorting algorithm
s that are much more efficient than insertion sort for large arrays.)
procedure zprec(r,s):
return (z[r] < z[s])
procedure zswap(r,s):
float t; t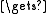 z[r]; z[r]
z[r]; z[r] 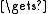 z[s]; z[s]
z[s]; z[s]  t
t
integer i
procedure eoprec(r, s):
return (M[i,r] mod 2) < (M[i,s] mod 2)
procedure eoswap(r, s):
integer t; t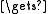 M[i,r]; M[i,r]
M[i,r]; M[i,r] 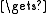 M[i,s]; M[i,s]
M[i,s]; M[i,s] 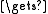 t
t
for i from 1 to 10 do
isort(1, 20, eoprec, eoswap)
Note that the effects of eoprec and eoswap depend on the row number i, but the isort procedure does not need to know that.
procedure vecsort(n, v, incr):
procedure vprec(r, s):
if incr then
return v[r] < v[s]
else
return v[r] > v[s]
procedure vswap(r, s):
integer t; t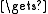 v[r]; v[r]
v[r]; v[r] 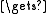 v[s]; v[s]
v[s]; v[s] 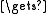 t
t
isort(0, n−1, vprec, vswap)
Note the use of nested function definitions to get a function vprec whose effect depends on the parameter incr passed to vecsort. In languages that do not allow nested function definitions, like standard C, obtaining this effect would require rather complicated and/or thread-unsafe code.
procedure merge(A, B, prec, nextA, appendA, nextB, appendB):
address ini, fin, t
ini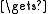 Λ; fin
Λ; fin 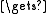 Λ
Λ
while A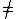 Λ or B
Λ or B  Λ do
Λ do
if B Λ or (A
Λ or (A 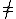 Λ and B
Λ and B 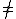 Λ and prec(A,B)) then
Λ and prec(A,B)) then
t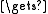 nextA(A)
nextA(A)
fin appendA(A, fin); if ini
appendA(A, fin); if ini  Λ then ini
Λ then ini 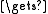 fin
fin
A t
t
else
t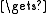 nextB(B)
nextB(B)
fin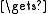 appendB(B, fin); if ini
appendB(B, fin); if ini  Λ then ini
Λ then ini  fin
fin
B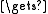 t
t
return ini
The function prec should take the addresses r, s of two records, one from each sequence, and return true if the first record should come before the other in the output sequence. The function nextA should take the address of a record from the first sequence, and return the address of the next record in the same sequence, or Λ if there is none. The function appendA should append the first record from sequence A to the output sequence; its arguments are the address A of the record to be appended, and the address fin of the last record of the output list (or Λ if that list is still empty). The procedure appendA should return the updated address of the final element of the output list. The procedures nextB and appendB are analogous for the other input sequence.
s, starting with nodes at addresses R, S. Here we assume that each record x contains an integer field x.INFO and an address field x.NEXT that points to the next node; where the info fields are in increasing order in each list. The input lists are dismantled by the merge, and their nodes are used to build the output list.
procedure listmerge(R, S):
procedure prec(r, s):
return r.INFO < s.INFO
procedure next(x):
return x.NEXT
procedure append(x, fin)
if fin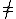 Λ then fin.NEXT
Λ then fin.NEXT 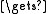 x
x
x.NEXT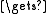 Λ
Λ
return x
return merge(R, S, prec, next, append, next, append)
procedure arraymerge(U, m, V, n, W):
procedure prec(r, s):
return (*r) > (*s)
procedure nextU(x):
if x = &(U[m−1]) then return Λ else return x + 1
procedure nextV(x):
if x = &(V[n−1]) then return Λ else return x + 1
procedure append(x, fin)
if fin Λ then fin
Λ then fin  &(W[0])
&(W[0])
(*fin)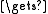 (*x)
(*x)
return fin + 1
if m = 0 then U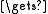 Λ
Λ
if n = 0 then V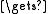 Λ
Λ
return merge(U, V, prec, nextU, append, nextV, append)
 f (x) dx of a given real-valued function
f (x) dx of a given real-valued function
f over a given interval [a,b] of the real line
. The numerical method used is the trapezium rule with a given number n of steps; the real numbers are approximated by floating-point numbers.
procedure Intg(f, a, b, n):
float t, x, s; integer i
if b = a then return 0
x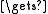 a; s
a; s 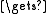 f(a)/2;
f(a)/2;
for i from 1 to n−1 do
t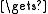 i/(n+1); x
i/(n+1); x 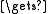 (1−t)*a + t*b;
(1−t)*a + t*b;
s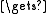 s + f(x)
s + f(x)
s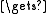 f(b)/2
f(b)/2
return (b−a)*s/n
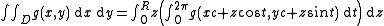
The following code implements the right-hand-side formula
:
procedure DiskIntg(g, xc, yc, R, n)
procedure gring(z):
procedure gpolar(t):
float x, y
x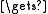 xc + z*cos(t)
xc + z*cos(t)
y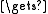 yc + z*sin(t)
yc + z*sin(t)
return g(x, y)
integer m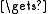 round(n*z/R)
round(n*z/R)
return z*Intg(gpolar, 0, 2*π, m)
return Intg(gring, 0, R, n)
This code uses the integration procedure Intg in two levels. The outer level (last line) uses Intg to compute the integral of gring(z) for z varying from 0 to R. The inner level (next-to-last line) defines gring(z) as being the line integral
of g(x,y) over the circle with center (xc,yc) and radius z.
Alonzo Church
, as part of his lambda calculus
model of computation.
Procedural parameters as a programming language feature were introduced by ALGOL 60. In fact, ALGOL 60 had a powerful "call by name" parameter-passing mechanism that could simplify some uses of procedural parameters; see Jensen's Device
.
Procedural parameters were an essential feature of the LISP programming language
, which also introduced the concept of function closure or funarg. The C programming language allows function pointers to be passed as parameters, which accomplish the same end, and are often used as callbacks in event-driven programming and as error handlers. However, only a few modern C compilers allow nested function definitions, so that its other uses are relatively uncommon. Procedural parameters were provided also in Pascal, together with nested procedure definitions; however, since standard Pascal did not allow separate compilation, the feature was little used in that language, too.
Computing
Computing is usually defined as the activity of using and improving computer hardware and software. It is the computer-specific part of information technology...
, a procedural parameter is a parameter
Parameter (computer science)
In computer programming, a parameter is a special kind of variable, used in a subroutine to refer to one of the pieces of data provided as input to the subroutine. These pieces of data are called arguments...
of a procedure
Subroutine
In computer science, a subroutine is a portion of code within a larger program that performs a specific task and is relatively independent of the remaining code....
that is itself a procedure.
This concept is an extremely powerful and versatile programming tool, because it allows programmers to modify certain steps of a library procedure
Library (computer science)
In computer science, a library is a collection of resources used to develop software. These may include pre-written code and subroutines, classes, values or type specifications....
in arbitrarily complicated ways, without having to understand or modify the code of that procedure.
This tool is particularly effective and convenient in languages that support local function definitions
Nested function
In computer programming, a nested function is a function which is lexically encapsulated within another function. It can only be called by the enclosing function or by functions directly or indirectly nested within the same enclosing function. In other words, the scope of the nested function is...
, such as Pascal and the modern GNU dialect
GNU Compiler Collection
The GNU Compiler Collection is a compiler system produced by the GNU Project supporting various programming languages. GCC is a key component of the GNU toolchain...
of C. It is even more so when function closures
Closure (computer science)
In computer science, a closure is a function together with a referencing environment for the non-local variables of that function. A closure allows a function to access variables outside its typical scope. Such a function is said to be "closed over" its free variables...
are available. The same functionality (and more) is provided by objects in object oriented programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s, but at a significantly higher cost.
Basic concept
In most languages that provide this feature, a procedural parameter f of a subroutine P can be called inside the body of P as if it were an ordinary procedure:procedure P(f):
return f(6,3) * f(2,1)
When calling the subroutine P, one must give it one argument, that must be some previously defined function compatible with the way P uses its parameter f. For example, if we define
procedure plus(x, y):
return x + y
then we may call P (plus), and the result will be plus(6,3) * plus(2,1) = (6 + 3)*(2 + 1) = 27. On the other hand, if we define
procedure quot(u, v):
return u/v
then the call P (quot) will return quot(6,3)*quot(2,1) = (6/3)*(2/1) = 4. Finally, if we define
procedure evil(z)
return z + 100
then the call P (evil) will not make much sense, and may be flagged as an error.
Syntactic details
Some programming languages that have this feature may allow or require a complete type declaration for each procedural parameter f, including the number and type of its arguments, and the type of its result, if any. For example, in the C programming language the example above could be written asint P ( int f (int a, int b) )
{ return f(6,3) * f(2,1); }
In principle, the actual function actf that is passed as argument when P is called must be type-compatible with the declared type of the procedure parameter f. This usually means that actf and f must return the same type of result, must have the same number of arguments, and corresponding arguments must have the same type. The names of the arguments need not be the same, however, as shown by the plus and quot examples above. However, some programming languages may me more restrictive or more liberal in this regard.
Scoping
In languages that allow procedural parameters, the scoping rules are usually defined in such a way that procedural parameters are executed in their native scope. More precisely, suppose that the function actf is passed as argument to P, as its procedural parameter f; and f is then called from inside the body of P. While actf is being executed, it sees the environment of its definition.The implementation of these scoping rules is not trivial. By the time that actf is finally executed, the activation records where its environment variables live may be arbitrarily deep in the stack. This is the so-called downwards funarg problem.
Example: Generic insertion sort
The concept of procedural parameter is best explained by examples. A typical application is the following generic implementation of the insertion sortInsertion sort
Insertion sort is a simple sorting algorithm: a comparison sort in which the sorted array is built one entry at a time. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort...
algorithm, that takes two integer parameters a,b and two procedural parameters prec, swap:
procedure isort(a, b, prec, swap):
integer i, j;
i
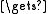 a;
a;while i
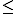 b do
b doj
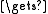 i
iwhile j > a and prec(j, j−1) do
swap(j, j−1); j
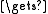 j−1
j−1i
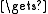 i+1
i+1This procedure can be used to sort the elements x[a] through x[b] of some array x, of arbitrary type, in a user-specified order. The parameters prec and swap should be two functions, defined by the client, both taking two integers r, s between a and b. The prec function should return true if and only if the data stored in x[r] should precede the data stored in x[s], in the ordering defined by the client. The swap function should exchange the contents of x[r] and x[s], and return no result.
By the proper choice of the functions prec and swap, the same isort procedure can be used to reorder arrays of any data type, stored in any medium and organized in any data structure that provides indexed access to individual array elements. (Note however that there are sorting algorithm
Sorting algorithm
In computer science, a sorting algorithm is an algorithm that puts elements of a list in a certain order. The most-used orders are numerical order and lexicographical order...
s that are much more efficient than insertion sort for large arrays.)
Sorting floating-point numbers
For instance, we can sort an array z of 20 floating-point numbers, z[1] through z[20] in increasing order by calling isort (1, 20,zprec,zswap), where the functions zprec and zswap are defined asprocedure zprec(r,s):
return (z[r] < z[s])
procedure zswap(r,s):
float t; t
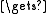 z[r]; z[r]
z[r]; z[r] 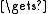 z[s]; z[s]
z[s]; z[s]  t
tSorting rows of a matrix
For another example, let M be a matrix of integers with 10 rows and 20 columns, with indices starting at 1. The following code will rearrange the elements in each row so that all the even values come before all odd values:integer i
procedure eoprec(r, s):
return (M[i,r] mod 2) < (M[i,s] mod 2)
procedure eoswap(r, s):
integer t; t
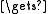 M[i,r]; M[i,r]
M[i,r]; M[i,r] 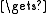 M[i,s]; M[i,s]
M[i,s]; M[i,s] 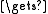 t
tfor i from 1 to 10 do
isort(1, 20, eoprec, eoswap)
Note that the effects of eoprec and eoswap depend on the row number i, but the isort procedure does not need to know that.
Vector-sorting procedure
The following example uses isort to define a procedure vecsort that takes an integer n and an integer vector v with elements v[0] through v[n−1] and sorts them in either increasing or decreasing order, depending on whether a third parameter incr is true or false, respectively:procedure vecsort(n, v, incr):
procedure vprec(r, s):
if incr then
return v[r] < v[s]
else
return v[r] > v[s]
procedure vswap(r, s):
integer t; t
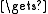 v[r]; v[r]
v[r]; v[r] 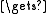 v[s]; v[s]
v[s]; v[s] 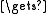 t
tisort(0, n−1, vprec, vswap)
Note the use of nested function definitions to get a function vprec whose effect depends on the parameter incr passed to vecsort. In languages that do not allow nested function definitions, like standard C, obtaining this effect would require rather complicated and/or thread-unsafe code.
Example: merging two sequences
The following example illustrates the use of procedural parameters to process abstract data structures independently of their concrete implementation. The problem is to merge two ordered sequences of records into a single sorted sequence, where the nature of the records and the ordering criterion can be chosen by the client. The following implementation assumes only that each record can be referenced by a memory address, and there is a "null address" Λ that is not the address of any valid record. The client must provide the addresses A, B of the first records in each sequence, and functions prec, next, and append, to be described later.procedure merge(A, B, prec, nextA, appendA, nextB, appendB):
address ini, fin, t
ini
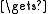 Λ; fin
Λ; fin 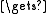 Λ
Λwhile A
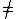 Λ or B
Λ or B  Λ do
Λ doif B
 Λ or (A
Λ or (A 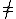 Λ and B
Λ and B 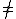 Λ and prec(A,B)) then
Λ and prec(A,B)) thent
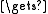 nextA(A)
nextA(A)fin
 appendA(A, fin); if ini
appendA(A, fin); if ini  Λ then ini
Λ then ini 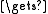 fin
finA
 t
telse
t
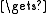 nextB(B)
nextB(B)fin
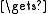 appendB(B, fin); if ini
appendB(B, fin); if ini  Λ then ini
Λ then ini  fin
finB
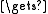 t
treturn ini
The function prec should take the addresses r, s of two records, one from each sequence, and return true if the first record should come before the other in the output sequence. The function nextA should take the address of a record from the first sequence, and return the address of the next record in the same sequence, or Λ if there is none. The function appendA should append the first record from sequence A to the output sequence; its arguments are the address A of the record to be appended, and the address fin of the last record of the output list (or Λ if that list is still empty). The procedure appendA should return the updated address of the final element of the output list. The procedures nextB and appendB are analogous for the other input sequence.
Merging linked lists
To illustrate the use of the generic merge procedure, here is the code for merging two simple linked listLinked list
In computer science, a linked list is a data structure consisting of a group of nodes which together represent a sequence. Under the simplest form, each node is composed of a datum and a reference to the next node in the sequence; more complex variants add additional links...
s, starting with nodes at addresses R, S. Here we assume that each record x contains an integer field x.INFO and an address field x.NEXT that points to the next node; where the info fields are in increasing order in each list. The input lists are dismantled by the merge, and their nodes are used to build the output list.
procedure listmerge(R, S):
procedure prec(r, s):
return r.INFO < s.INFO
procedure next(x):
return x.NEXT
procedure append(x, fin)
if fin
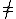 Λ then fin.NEXT
Λ then fin.NEXT 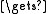 x
xx.NEXT
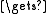 Λ
Λreturn x
return merge(R, S, prec, next, append, next, append)
Merging vectors
The following code illustrates the independence of the generic merge procedure from the actual representation of the sequences. It merges the elements of two ordinary arrays U[0] through U[m−1] and V[0] through V[n−1] of floating-point numbers, in decreasing order. The input arrays are not modified, and the merged sequence of values is stored into a third vector W[0] through W[m+n−1]. As in the C programming language, we assume that the expression "&V" yields the address of variable V, "*p" yields the variable whose address is the value of p, and that "&(X[i])" is equivalent to "&(X[0]) + i" for any array X and any integer i.procedure arraymerge(U, m, V, n, W):
procedure prec(r, s):
return (*r) > (*s)
procedure nextU(x):
if x = &(U[m−1]) then return Λ else return x + 1
procedure nextV(x):
if x = &(V[n−1]) then return Λ else return x + 1
procedure append(x, fin)
if fin
 Λ then fin
Λ then fin  &(W[0])
&(W[0])(*fin)
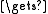 (*x)
(*x)return fin + 1
if m = 0 then U
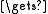 Λ
Λif n = 0 then V
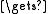 Λ
Λreturn merge(U, V, prec, nextU, append, nextV, append)
Integrating over an interval
The following procedure computes the approximate integral f (x) dx of a given real-valued function
f (x) dx of a given real-valued functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f over a given interval [a,b] of the real line
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
. The numerical method used is the trapezium rule with a given number n of steps; the real numbers are approximated by floating-point numbers.
procedure Intg(f, a, b, n):
float t, x, s; integer i
if b = a then return 0
x
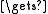 a; s
a; s 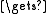 f(a)/2;
f(a)/2;for i from 1 to n−1 do
t
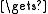 i/(n+1); x
i/(n+1); x 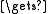 (1−t)*a + t*b;
(1−t)*a + t*b;s
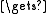 s + f(x)
s + f(x)s
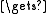 f(b)/2
f(b)/2return (b−a)*s/n
Integrating over a disk
Consider now the problem of integrating a given function g, with two arguments, over a disk D with given center (xc,yc) and given radius R. This problem can be reduced to two nested single-variable integrals by the change of variables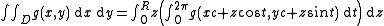
The following code implements the right-hand-side formula
Sides of an equation
In mathematics, LHS is informal shorthand for the left-hand side of an equation. Similarly, RHS is the right-hand side. Each is solely a name for a term as part of an expression; and they are in practice interchangeable, since equality is symmetric...
:
procedure DiskIntg(g, xc, yc, R, n)
procedure gring(z):
procedure gpolar(t):
float x, y
x
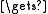 xc + z*cos(t)
xc + z*cos(t)y
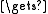 yc + z*sin(t)
yc + z*sin(t)return g(x, y)
integer m
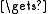 round(n*z/R)
round(n*z/R)return z*Intg(gpolar, 0, 2*π, m)
return Intg(gring, 0, R, n)
This code uses the integration procedure Intg in two levels. The outer level (last line) uses Intg to compute the integral of gring(z) for z varying from 0 to R. The inner level (next-to-last line) defines gring(z) as being the line integral
Line integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
of g(x,y) over the circle with center (xc,yc) and radius z.
History
Procedural parameters were invented before the age of electronic computers, by mathematicianMathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
Alonzo Church
Alonzo Church
Alonzo Church was an American mathematician and logician who made major contributions to mathematical logic and the foundations of theoretical computer science. He is best known for the lambda calculus, Church–Turing thesis, Frege–Church ontology, and the Church–Rosser theorem.-Life:Alonzo Church...
, as part of his lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
model of computation.
Procedural parameters as a programming language feature were introduced by ALGOL 60. In fact, ALGOL 60 had a powerful "call by name" parameter-passing mechanism that could simplify some uses of procedural parameters; see Jensen's Device
Jensen's Device
Jensen's Device is a computer programming technique devised by Danish computer scientist Jørn Jensen, who worked with Peter Naur at Regnecentralen, particularly on the GIER Algol compiler, one of the earliest correct implementations of ALGOL 60....
.
Procedural parameters were an essential feature of the LISP programming language
Lisp programming language
Lisp is a family of computer programming languages with a long history and a distinctive, fully parenthesized syntax. Originally specified in 1958, Lisp is the second-oldest high-level programming language in widespread use today; only Fortran is older...
, which also introduced the concept of function closure or funarg. The C programming language allows function pointers to be passed as parameters, which accomplish the same end, and are often used as callbacks in event-driven programming and as error handlers. However, only a few modern C compilers allow nested function definitions, so that its other uses are relatively uncommon. Procedural parameters were provided also in Pascal, together with nested procedure definitions; however, since standard Pascal did not allow separate compilation, the feature was little used in that language, too.
See also
- Functional programmingFunctional programmingIn computer science, functional programming is a programming paradigm that treats computation as the evaluation of mathematical functions and avoids state and mutable data. It emphasizes the application of functions, in contrast to the imperative programming style, which emphasizes changes in state...
- Funarg problemFunarg problemIn computer science, the funarg problem refers to the difficulty in implementing first-class functions in stack-based programming language implementations....
- Design patterns (computer science)

