A projective cone in projective geometry

Projective geometry

In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...

 is the union of all lines that intersect a projective subspace R (the apex of the cone) and an arbitrary subset A (the basis) of some other subspace S, disjoint from R.

In the special case that R is a single point, S is a plane, and A is a conic section

Conic section

In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...

 on S, the projective cone is a conical surface

Conical surface

In geometry, a conical surface is the unbounded surface formed by the union of all the straight lines that pass through a fixed point — the apex or vertex — and any point of some fixed space curve — the directrix — that does not contain the apex...

; hence the name.

Definition

Let X be a projective space over some field K, and R, S be disjoint subspaces of X. Let A be an arbitrary subset of S. Then we define RA, the cone with top R and basis A, as follows :

• When A is empty, RA = A.
• When A is not empty, RA consists of all those points
  Point (geometry)
  In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
  
   on a line connecting a point on R and a point on A.

Properties

• As R and S are disjoint, one easily sees that every point on RA not in R or A is on exactly one line connecting a point in R and a point in A.
• (RA) S = A
• When K = GF(q), = + .

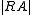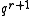
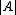See also

• Cone (geometry)
  Cone (geometry)
  A cone is an n-dimensional geometric shape that tapers smoothly from a base to a point called the apex or vertex. Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base...
  
  
• Cone (topology)
  Cone (topology)
  In topology, especially algebraic topology, the cone CX of a topological space X is the quotient space:CX = /\,of the product of X with the unit interval I = [0, 1]....
  
  
• Conic section
  Conic section
  In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
  
  
• Ruled surface
  Ruled surface
  In geometry, a surface S is ruled if through every point of S there is a straight line that lies on S. The most familiar examples are the plane and the curved surface of a cylinder or cone...
  
  
• Hyperboloid