Projective connection
Encyclopedia
In differential geometry, a projective connection is a type of Cartan connection
on a differentiable manifold
.
The structure of a projective connection is modeled on the geometry of projective space
, rather than the affine space
corresponding to an affine connection
. Much like affine connections, though, projective connections also define geodesics. However, these geodesics are not affinely parametrized. Rather they are projectively parametrized, meaning that their preferred class of parameterizations is acted upon by the group of fractional linear transformations.
Like an affine connection, projective connections have associated torsion and curvature.
on a homogeneous space
.
In the projective setting, the underlying manifold M of the homogeneous space is the projective space RPn which we shall represent by homogeneous coordinates
[x0,...,xn]. The symmetry group of M is G = PSL(n+1,R). Let H be the isotropy group of the point [1,0,0,...,0]. Thus, M = G/H presents M as a homogeneous space.
Let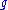
be the Lie algebra
of G, and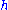
that of H. Note that 
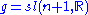. As matrices relative to the homogeneous basis, 
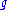consists of trace-free (n+1)×(n+1) matrices:
.
And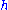
consists of all these matrices with (wj) = 0. Relative to the matrix representation above, the Maurer-Cartan form of G is a system of 1-forms (ζ, αj, αji, αi) satisfying the structural equations
s. According to Cartan (1924),
This is analogous to Cartan's notion of an affine connection
, in which nearby points are thus connected and have an affine frame of reference
which is transported from one to the other (Cartan, 1923):
In modern language, a projective structure on an n-manifold M is a Cartan geometry modelled on projective space, where the latter is viewed as a homogeneous space for PSL(n+1,R). In other words it is a PSL(n+1,R)-bundle equipped with
such that the solder form
induced by these data is an isomorphism.
Cartan connection
In the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the...
on a differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
.
The structure of a projective connection is modeled on the geometry of projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
, rather than the affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
corresponding to an affine connection
Affine connection
In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
. Much like affine connections, though, projective connections also define geodesics. However, these geodesics are not affinely parametrized. Rather they are projectively parametrized, meaning that their preferred class of parameterizations is acted upon by the group of fractional linear transformations.
Like an affine connection, projective connections have associated torsion and curvature.
Projective space as the model geometry
The first step in defining any Cartan connection is to consider the flat case: in which the connection corresponds to the Maurer-Cartan formMaurer-Cartan form
In mathematics, the Maurer–Cartan form for a Lie group G is a distinguished differential one-form on G that carries the basic infinitesimal information about the structure of G...
on a homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
.
In the projective setting, the underlying manifold M of the homogeneous space is the projective space RPn which we shall represent by homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
[x0,...,xn]. The symmetry group of M is G = PSL(n+1,R). Let H be the isotropy group of the point [1,0,0,...,0]. Thus, M = G/H presents M as a homogeneous space.
Let
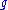be the Lie algebraLie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of G, and
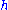that of H. Note that 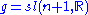. As matrices relative to the homogeneous basis, 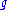consists of trace-free (n+1)×(n+1) matrices:.And
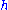consists of all these matrices with (wj) = 0. Relative to the matrix representation above, the Maurer-Cartan form of G is a system of 1-forms (ζ, αj, αji, αi) satisfying the structural equations
- dζ + ∑i αi∧αi = 0
- dαj + αj∧ζ + ∑k αjk∧αk = 0
- dαji + αi∧αj + ∑k αki∧αjk = 0
- dαi + ζ∧αi + ∑kαk∧αki = 0
Projective structures on manifolds
A projective structure is a linear geometry on a manifold in which two nearby points are connected by a line (i.e., an unparametrized geodesic) in a unique manner. Furthermore, an infinitesimal neighborhood of each point is equipped with a class of projective frameProjective frame
In the mathematical field of projective geometry, a projective frame is an ordered collection of points in projective space which can be used as reference points to describe any other point in that space...
s. According to Cartan (1924),
- Une variété (ou espace) à connexion projective est une variété numérique qui, au voisinage immédiat de chaque point, présente tous les caractères d'un espace projectif et douée de plus d'une loi permettant de raccorder en un seul espace projectif les deux petits morceaux qui entourent deux points infiniment voisins. ..
- Analytiquement, on choisira, d'une manière d'ailleurs arbitraire, dans l'espace projectif attaché à chaque point a de la variété, un repére définissant un système de coordonnées projectives. .. Le raccord entre les espaces projectifs attachés à deux points infiniment voisins a et a' se traduira analytiquement par une transformation homographique. ..
This is analogous to Cartan's notion of an affine connection
Affine connection
In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
, in which nearby points are thus connected and have an affine frame of reference
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
which is transported from one to the other (Cartan, 1923):
- La variété sera dite à "connexion affine" lorsqu'on aura défini, d'une manière d'ailleurs arbitraire, une loi permettant de repérer l'un par rapport à l'autre les espaces affines attachés à deux points infiniment voisins quelconques m et m' de la variété; cete loi permettra de dire que tel point de l'espace affine attaché au point m' correspond à tel point de l'espace affine attaché au point m, que tel vecteur du premier espace es parallèle ou équipollent à tel vecteur du second espace.
In modern language, a projective structure on an n-manifold M is a Cartan geometry modelled on projective space, where the latter is viewed as a homogeneous space for PSL(n+1,R). In other words it is a PSL(n+1,R)-bundle equipped with
- a PSL(n+1,R)-connection (the Cartan connectionCartan connectionIn the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the...
) - a reduction of structure group to the stabilizer of a point in projective space
such that the solder form
Solder form
In mathematics, more precisely in differential geometry, a soldering of a fibre bundle to a smooth manifold is a manner of attaching the fibres to the manifold in such a way that they can be regarded as tangent...
induced by these data is an isomorphism.