Projective cover
Encyclopedia
In the branch of abstract mathematics called category theory
, a projective cover of an object X is in a sense the best approximation of X by a projective object P. Projective covers are the dual
of injective envelopes.
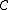be a category
and X an object in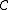
. A projective cover is a pair (P,p), with P a projective object in 
and p a superfluous epimorphism in Hom(P, X).
If R is a ring, then in the category of R-modules, a superfluous epimorphism is then an epimorphism
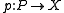such that the kernel
of p is a superfluous submodule of P.
.
The main effect of p having a superfluous kernel is the following: if N is any proper submodule of P, then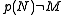
. Informally speaking, the superfluous kernel causes P to cover M optimally, in some sense. This does not depend upon the projectivity of P, it is true of all superfluous epimorphisms.
If (P,p) is a projective cover of M, and P' is another projective module with an epimorphism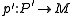
, then there is a split epimorphism α from P' to P such that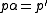 
Unlike injective envelopes, which exist for every left (right) R-module
regardless of the ring
R, left (right) R-modules do not in general have projective covers. A ring R is called left (right) perfect
if every left (right) R-module has a projective cover in R-Mod (Mod-R).
A ring is called semiperfect
if every finitely generated left (right) R-module has a projective cover in R-Mod (Mod-R). "Semiperfect" is a left-right symmetric property.
A ring is called lift/rad if idempotents lift from R/J to R, where J is the Jacobson radical
of R. The property of being lift/rad can be characterized in terms of projective covers: R is lift/rad if and only if direct summands of the R module R/J (as a right or left module) have projective covers.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a projective cover of an object X is in a sense the best approximation of X by a projective object P. Projective covers are the dual
Dual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
of injective envelopes.
Definition
Let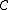 be a categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
and X an object in
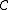. A projective cover is a pair (P,p), with P a projective object in and p a superfluous epimorphism in Hom(P, X).If R is a ring, then in the category of R-modules, a superfluous epimorphism is then an epimorphism
Epimorphism
In category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
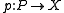such that the kernelKernel (algebra)
In the various branches of mathematics that fall under the heading of abstract algebra, the kernel of a homomorphism measures the degree to which the homomorphism fails to be injective. An important special case is the kernel of a matrix, also called the null space.The definition of kernel takes...
of p is a superfluous submodule of P.
Properties
Projective covers and their superfluous epimorphisms, when they exist, are unique up to isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
.
The main effect of p having a superfluous kernel is the following: if N is any proper submodule of P, then
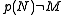. Informally speaking, the superfluous kernel causes P to cover M optimally, in some sense. This does not depend upon the projectivity of P, it is true of all superfluous epimorphisms.If (P,p) is a projective cover of M, and P' is another projective module with an epimorphism
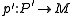, then there is a split epimorphism α from P' to P such that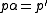 Unlike injective envelopes, which exist for every left (right) R-module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
regardless of the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R, left (right) R-modules do not in general have projective covers. A ring R is called left (right) perfect
Perfect ring
In the area of abstract algebra known as ring theory, a left perfect ring is a type of ring in which all left modules have projective covers. The right case is defined by analogy, and the condition is not left-right symmetric, that is, there exist rings which are perfect on one side but not the...
if every left (right) R-module has a projective cover in R-Mod (Mod-R).
A ring is called semiperfect
Semiperfect ring
In abstract algebra, a semiperfect ring is a ring over which every finitely generated left module has a projective cover. This property is left right symmetric.- Definition :Let R be ring...
if every finitely generated left (right) R-module has a projective cover in R-Mod (Mod-R). "Semiperfect" is a left-right symmetric property.
A ring is called lift/rad if idempotents lift from R/J to R, where J is the Jacobson radical
Jacobson radical
In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...
of R. The property of being lift/rad can be characterized in terms of projective covers: R is lift/rad if and only if direct summands of the R module R/J (as a right or left module) have projective covers.
Examples
In the category of R modules:- If M is already a projective module, then the identity map from M to M is a superfluous epimorphism (its kernel being zero). Hence, projective modules always have projective covers.
- If J(R)=0, then a module M has a projective cover if and only if M is already projective.
- In the case that a module M is simpleSimple moduleIn mathematics, specifically in ring theory, the simple modules over a ring R are the modules over R which have no non-zero proper submodules. Equivalently, a module M is simple if and only if every cyclic submodule generated by a non-zero element of M equals M...
, then it is necessarily the topTop (mathematics)In the context of a module M over a ring R, the top of M is the largest semisimple quotient module of M if it exists.For finite-dimensional k-algebras , if rad denotes the intersection of all proper maximal submodules of M , then the top of M is M/rad...
of its projective cover, if it exists. - The injective envelope for a module always exists, however over certain rings modules may not have projective covers. The class of rings which provides all of its right modules with projective covers is the class of right perfect ringPerfect ringIn the area of abstract algebra known as ring theory, a left perfect ring is a type of ring in which all left modules have projective covers. The right case is defined by analogy, and the condition is not left-right symmetric, that is, there exist rings which are perfect on one side but not the...
s.