Propagation constant
Encyclopedia
The propagation constant of an electromagnetic wave is a measure of the change undergone by the amplitude of the wave as it propagates
in a given direction. The quantity being measured can be the voltage
or current
in a circuit or a field vector such as electric field strength or flux density
. The propagation constant itself measures change per metre but is otherwise dimensionless.
The propagation constant is expressed logarithmically, almost universally to the base e, rather than the more usual base 10 used in telecommunication
s in other situations. The quantity measured, such as voltage, is expressed as a sinusoidal phasor
. The phase of the sinusoid varies with distance which results in the propagation constant being a complex number
, the imaginary
part being caused by the phase change.
theory, the term secondary being used to contrast to the primary line coefficients. The primary coefficients being the physical properties of the line; R,C,L and G, from which the secondary coefficients may be derived using the telegrapher's equation. Note that, at least in the field of transmission lines, the term transmission coefficient
has a different meaning despite the similarity of name. Here it is the corollary of reflection coefficient
.
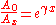
Since the propagation constant is a complex quantity we can write:
where
That β does indeed represent phase can be seen from Euler's formula
;
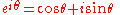
which is a sinusoid which varies in phase as θ varies but does not vary in amplitude because;
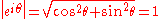
The reason for the use of base e is also now made clear. The imaginary phase constant, iβ, can be added directly to the attenuation constant, α, to form a single complex number that can be handled in one mathematical operation provided they are to the same base. Angles measured in radians require base e, so the attenuation is likewise in base e.
The propagation constant for copper (or any other conductor) lines can be calculated from the primary line coefficients by means of the relationship;
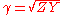
where;
, the series impedance
of the line per metre and,
, the shunt admittance
of the line per metre.
s, the term attenuation constant, also called attenuation parameter or coefficient, is the attenuation of an electromagnetic wave propagating through a medium
per unit distance from the source. It is the real part of the propagation constant and is measured in nepers per metre. A neper is approximately 8.7dB
. Attenuation constant can be defined by the amplitude ratio;
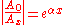
The propagation constant per unit length is defined as the natural logarithmic of ratio of the sending end current or voltage to the receiving end current or voltage.
, with a conductance G in the insulator, the attenuation constant is given by;
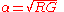
however, a real line is unlikely to meet this condition without the addition of loading coils and, furthermore, there are some frequency dependant effects operating on the primary "constants" which cause a frequency dependence of the loss. There are two main components to these losses, the metal loss and the dielectric loss.
The loss of most transmission lines are dominated by the metal loss, which causes a frequency dependency due to finite conductivity of metals, and the skin effect
inside a conductor. The skin effect causes R along the conductor to be approximately dependent on frequency according to;
Losses in the dielectric depend on the loss tangent
(
) of the material, which depends inversely on the wavelength of the signal and is directly proportional to the frequency.
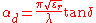
, the real part of the axial propagation constant.
From the definition of (angular) wavenumber;
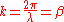
For a transmission line
, the Heaviside condition
of the telegrapher's equation tells us that the wavenumber must be proportional to frequency for the transmission of the wave to be undistorted in the time domain
. This includes, but is not limited to, the ideal case of a lossless line. The reason for this condition can be seen by considering that a useful signal is composed of many different wavelengths in the frequency domain. For there to be no distortion of the waveform
, all these waves must travel at the same velocity so that they arrive at the far end of the line at the same time as a group
. Since wave phase velocity
is given by;
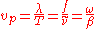
it is proved that β is required to be proportional to ω. In terms of primary coefficients of the line, this yields from the telegrapher's equation for a distortionless line the condition;
However, practical lines can only be expected to approximately meet this condition over a limited frequency band.
s used for signal processing
. In these cases, however, the attenuation and phase coefficients are expressed in terms of nepers and radians per network section rather than per metre. Some authors make a distinction between per metre measures (for which "constant" is used) and per section measures (for which "function" is used).
The propagation constant is a useful concept in filter design which invariably uses a cascaded section topology
. In a cascaded topology, the propagation constant, attenuation constant and phase constant of individual sections may be simply added to find the total propagation constant etc.
The ratio of output to input voltage for each network is given by,
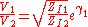
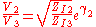
The terms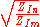
are impedance scaling terms and their use is explained in the image impedance article.
The overall voltage ratio is given by,
Thus for n cascaded sections all having matching impedances facing each other, the overall propagation constant is given by,
.
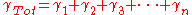
Wave propagation
Wave propagation is any of the ways in which waves travel.With respect to the direction of the oscillation relative to the propagation direction, we can distinguish between longitudinal wave and transverse waves....
in a given direction. The quantity being measured can be the voltage
Voltage
Voltage, otherwise known as electrical potential difference or electric tension is the difference in electric potential between two points — or the difference in electric potential energy per unit charge between two points...
or current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
in a circuit or a field vector such as electric field strength or flux density
Flux density
-Formal Statement:The flux density is simply defined as the amount of flux passing through a unit-area. -Mathematical Statement:The flux density would essentially be the number of field lines passing through a defined unit-area...
. The propagation constant itself measures change per metre but is otherwise dimensionless.
The propagation constant is expressed logarithmically, almost universally to the base e, rather than the more usual base 10 used in telecommunication
Telecommunication
Telecommunication is the transmission of information over significant distances to communicate. In earlier times, telecommunications involved the use of visual signals, such as beacons, smoke signals, semaphore telegraphs, signal flags, and optical heliographs, or audio messages via coded...
s in other situations. The quantity measured, such as voltage, is expressed as a sinusoidal phasor
Phasor
Phasor is a phase vector representing a sine wave.Phasor may also be:* Phasor , a stereo music, sound and speech synthesizer for the Apple II computer* Phasor measurement unit, a device that measures phasors on an electricity grid...
. The phase of the sinusoid varies with distance which results in the propagation constant being a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
, the imaginary
Imaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
part being caused by the phase change.
Alternative names
The term propagation constant is somewhat of a misnomer as it usually varies strongly with ω. It is probably the most widely used term but there are a large variety of alternative names used by various authors for this quantity. These include, transmission parameter, transmission function, propagation parameter, propagation coefficient and transmission constant. In plural, it is usually implied that α and β are being referenced separately but collectively as in transmission parameters, propagation parameters, propagation coefficients, transmission constants and secondary coefficients. This last occurs in transmission lineTransmission line
In communications and electronic engineering, a transmission line is a specialized cable designed to carry alternating current of radio frequency, that is, currents with a frequency high enough that its wave nature must be taken into account...
theory, the term secondary being used to contrast to the primary line coefficients. The primary coefficients being the physical properties of the line; R,C,L and G, from which the secondary coefficients may be derived using the telegrapher's equation. Note that, at least in the field of transmission lines, the term transmission coefficient
Transmission coefficient
The transmission coefficient is used in physics and electrical engineering when wave propagation in a medium containing discontinuities is considered...
has a different meaning despite the similarity of name. Here it is the corollary of reflection coefficient
Reflection coefficient
The reflection coefficient is used in physics and electrical engineering when wave propagation in a medium containing discontinuities is considered. A reflection coefficient describes either the amplitude or the intensity of a reflected wave relative to an incident wave...
.
Definition
The propagation constant, symbol γ, for a given system is defined by the ratio of the amplitude at the source of the wave to the amplitude at some distance x, such that,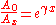Since the propagation constant is a complex quantity we can write:
where
- α, the real part, is called the attenuation constant
- β, the imaginary part, is called the phase constant
That β does indeed represent phase can be seen from Euler's formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
;
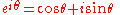
which is a sinusoid which varies in phase as θ varies but does not vary in amplitude because;
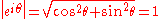
The reason for the use of base e is also now made clear. The imaginary phase constant, iβ, can be added directly to the attenuation constant, α, to form a single complex number that can be handled in one mathematical operation provided they are to the same base. Angles measured in radians require base e, so the attenuation is likewise in base e.
The propagation constant for copper (or any other conductor) lines can be calculated from the primary line coefficients by means of the relationship;
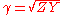
where;
, the series impedanceElectrical impedance
Electrical impedance, or simply impedance, is the measure of the opposition that an electrical circuit presents to the passage of a current when a voltage is applied. In quantitative terms, it is the complex ratio of the voltage to the current in an alternating current circuit...
of the line per metre and,
, the shunt admittanceAdmittance
In electrical engineering, the admittance is a measure of how easily a circuit or device will allow a current to flow. It is defined as the inverse of the impedance . The SI unit of admittance is the siemens...
of the line per metre.
Attenuation constant
In telecommunicationTelecommunication
Telecommunication is the transmission of information over significant distances to communicate. In earlier times, telecommunications involved the use of visual signals, such as beacons, smoke signals, semaphore telegraphs, signal flags, and optical heliographs, or audio messages via coded...
s, the term attenuation constant, also called attenuation parameter or coefficient, is the attenuation of an electromagnetic wave propagating through a medium
Transmission medium
A transmission medium is a material substance that can propagate energy waves...
per unit distance from the source. It is the real part of the propagation constant and is measured in nepers per metre. A neper is approximately 8.7dB
Decibel
The decibel is a logarithmic unit that indicates the ratio of a physical quantity relative to a specified or implied reference level. A ratio in decibels is ten times the logarithm to base 10 of the ratio of two power quantities...
. Attenuation constant can be defined by the amplitude ratio;
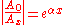
The propagation constant per unit length is defined as the natural logarithmic of ratio of the sending end current or voltage to the receiving end current or voltage.
Copper lines
The attenuation constant for copper lines (or ones made of any other conductor) can be calculated from the primary line coefficients as shown above. For a line meeting the distortionless conditionHeaviside condition
The Heaviside condition, due to Oliver Heaviside , is the condition an electrical transmission line must meet in order for there to be no distortion of a transmitted signal...
, with a conductance G in the insulator, the attenuation constant is given by;
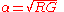
however, a real line is unlikely to meet this condition without the addition of loading coils and, furthermore, there are some frequency dependant effects operating on the primary "constants" which cause a frequency dependence of the loss. There are two main components to these losses, the metal loss and the dielectric loss.
The loss of most transmission lines are dominated by the metal loss, which causes a frequency dependency due to finite conductivity of metals, and the skin effect
Skin effect
Skin effect is the tendency of an alternating electric current to distribute itself within a conductor with the current density being largest near the surface of the conductor, decreasing at greater depths. In other words, the electric current flows mainly at the "skin" of the conductor, at an...
inside a conductor. The skin effect causes R along the conductor to be approximately dependent on frequency according to;
Losses in the dielectric depend on the loss tangent
Loss tangent
The loss tangent is a parameter of a dielectric material that quantifies its inherent dissipation of electromagnetic energy. The term refers to the tangent of the angle in a complex plane between the resistive component of an electromagnetic field and its reactive component.-Electromagnetic...
(
) of the material, which depends inversely on the wavelength of the signal and is directly proportional to the frequency.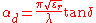Optical fibre
The attenuation constant for a particular propagation mode in an optical fiberOptical fiber
An optical fiber is a flexible, transparent fiber made of a pure glass not much wider than a human hair. It functions as a waveguide, or "light pipe", to transmit light between the two ends of the fiber. The field of applied science and engineering concerned with the design and application of...
, the real part of the axial propagation constant.
Phase constant
In electromagnetic theory, the phase constant, also called phase change constant, parameter or coefficient is the imaginary component of the propagation constant for a plane wave. It represents the change in phase per metre along the path travelled by the wave at any instant and is equal to real part of the angular wavenumber of the wave. It is represented by the symbol β and is measured in units of radians per metre.From the definition of (angular) wavenumber;
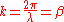
For a transmission line
Transmission line
In communications and electronic engineering, a transmission line is a specialized cable designed to carry alternating current of radio frequency, that is, currents with a frequency high enough that its wave nature must be taken into account...
, the Heaviside condition
Heaviside condition
The Heaviside condition, due to Oliver Heaviside , is the condition an electrical transmission line must meet in order for there to be no distortion of a transmitted signal...
of the telegrapher's equation tells us that the wavenumber must be proportional to frequency for the transmission of the wave to be undistorted in the time domain
Time domain
Time domain is a term used to describe the analysis of mathematical functions, physical signals or time series of economic or environmental data, with respect to time. In the time domain, the signal or function's value is known for all real numbers, for the case of continuous time, or at various...
. This includes, but is not limited to, the ideal case of a lossless line. The reason for this condition can be seen by considering that a useful signal is composed of many different wavelengths in the frequency domain. For there to be no distortion of the waveform
Waveform
Waveform means the shape and form of a signal such as a wave moving in a physical medium or an abstract representation.In many cases the medium in which the wave is being propagated does not permit a direct visual image of the form. In these cases, the term 'waveform' refers to the shape of a graph...
, all these waves must travel at the same velocity so that they arrive at the far end of the line at the same time as a group
Group velocity
The group velocity of a wave is the velocity with which the overall shape of the wave's amplitudes — known as the modulation or envelope of the wave — propagates through space....
. Since wave phase velocity
Phase velocity
The phase velocity of a wave is the rate at which the phase of the wave propagates in space. This is the speed at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave will appear to travel at the phase velocity...
is given by;
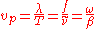
it is proved that β is required to be proportional to ω. In terms of primary coefficients of the line, this yields from the telegrapher's equation for a distortionless line the condition;
However, practical lines can only be expected to approximately meet this condition over a limited frequency band.
Filters
The term propagation constant or propagation function is applied to filters and other two-port networkTwo-port network
A two-port network is an electrical circuit or device with two pairs of terminals connected together internally by an electrical network...
s used for signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
. In these cases, however, the attenuation and phase coefficients are expressed in terms of nepers and radians per network section rather than per metre. Some authors make a distinction between per metre measures (for which "constant" is used) and per section measures (for which "function" is used).
The propagation constant is a useful concept in filter design which invariably uses a cascaded section topology
Electronic filter topology
Electronic filter topology defines electronic filter circuits without taking note of the values of the components used but only the manner in which those components are connected....
. In a cascaded topology, the propagation constant, attenuation constant and phase constant of individual sections may be simply added to find the total propagation constant etc.
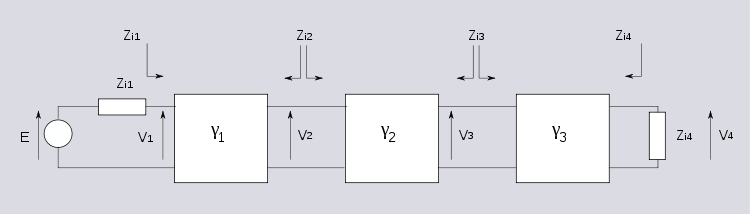
Cascaded networks
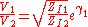
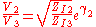
The terms
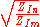are impedance scaling terms and their use is explained in the image impedance article.The overall voltage ratio is given by,
Thus for n cascaded sections all having matching impedances facing each other, the overall propagation constant is given by,
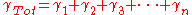
See also
The concept of penetration depth is one of many ways to describe the absorption of electromagnetic waves. For the others, and their interrelationships, see the article: Mathematical descriptions of opacityMathematical descriptions of opacity
When an electromagnetic wave travels through a medium in which it gets absorbed , it undergoes exponential decay as described by the Beer–Lambert law. However, there are many possible ways to characterize the wave and how quickly it is absorbed...
.