Propositional directed acyclic graph
Encyclopedia
A propositional directed acyclic graph (PDAG) is a data structure
that is used to represent a Boolean function. A Boolean function can be represented as a rooted, directed acyclic graph
of the following form:
Leaves labeled with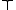
(
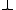) represent the constant Boolean function which always evaluates to 1 (0). A leaf labeled with a Boolean variable 
is interpreted as the assignment 
, i.e. it represents the Boolean function which evaluates to 1 if and only if 
. The Boolean function represented by a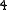 
-node is the one that evaluates to 1, if and only if the Boolean function of all its children evaluate to 1. Similarly, a 
-node represents the Boolean function that evaluates to 1, if and only if the Boolean function of at least one child evaluates to 1. Finally, a 
-node represents the complemenatary Boolean function its child, i.e. the one that evaluates to 1, if and only if the Boolean function of its child evaluates to 0.
and every negation normal form (NNF) is also a PDAG with some particular properties. The following pictures represent the Boolean function
:
Data structure
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
that is used to represent a Boolean function. A Boolean function can be represented as a rooted, directed acyclic graph
Directed acyclic graph
In mathematics and computer science, a directed acyclic graph , is a directed graph with no directed cycles. That is, it is formed by a collection of vertices and directed edges, each edge connecting one vertex to another, such that there is no way to start at some vertex v and follow a sequence of...
of the following form:
- Leaves are labeled with
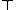(true), 
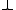(false), or a Boolean variable. - Non-leaves are
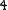(logical and), 
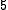(logical or) and 
(logical not). -
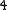- and 
-nodes have at least one child. -
-nodes have exactly one child.
Leaves labeled with
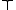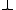() represent the constant Boolean function which always evaluates to 1 (0). A leaf labeled with a Boolean variable is interpreted as the assignment , i.e. it represents the Boolean function which evaluates to 1 if and only if . The Boolean function represented by a 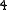-node is the one that evaluates to 1, if and only if the Boolean function of all its children evaluate to 1. Similarly, a -node represents the Boolean function that evaluates to 1, if and only if the Boolean function of at least one child evaluates to 1. Finally, a -node represents the complemenatary Boolean function its child, i.e. the one that evaluates to 1, if and only if the Boolean function of its child evaluates to 0.PDAG, BDD, and NNF
Every binary decision diagram (BDD)Binary decision diagram
In the field of computer science, a binary decision diagram or branching program, like a negation normal form or a propositional directed acyclic graph , is a data structure that is used to represent a Boolean function. On a more abstract level, BDDs can be considered as a compressed...
and every negation normal form (NNF) is also a PDAG with some particular properties. The following pictures represent the Boolean function
:  |
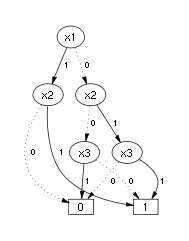See also
- Data structureData structureIn computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
- Boolean satisfiability problemBoolean satisfiability problemIn computer science, satisfiability is the problem of determining if the variables of a given Boolean formula can be assigned in such a way as to make the formula evaluate to TRUE...
- Proposition