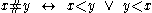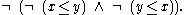Pseudo-order
Encyclopedia
In constructive mathematics
, a pseudo-order is a constructive generalisation of a linear order to the continuous case. The usual trichotomy law does not hold in the constructive continuum because of its indecomposability
, so this condition is weakened.
A pseudo-order is a binary relation
satisfying the following conditions:
This first condition is simply asymmetry
. It follows from the first two conditions that a pseudo-order is transitive
. The second condition is often called co-transitivity or comparison and is the constructive substitute for trichotomy. In general, given two elements of a pseudo-ordered set, it is not always the case that either one is less than the other or else they are equal, but given any nontrivial interval, any element is either above the lower bound, or below the upper bound.
The third condition is often taken as the definition of equality. The natural apartness relation
on a pseudo-ordered set is given by
and equality is defined by the negation of apartness.
The negation of the pseudo-order is a partial order which is close to a total order
: if x ≤ y is defined as the negation of y < x, then we have
Using classical logic
one would then conclude that x ≤ y or y ≤ x, so it would be a total order. However, this inference is not valid in the constructive case.
The prototypical pseudo-order is that of the real numbers: one real number is less than another if there exists (one can construct) a rational number greater than the former and less than the latter. In other words, x < y if there exists a rational number z such that x < z < y.
Constructivism (mathematics)
In the philosophy of mathematics, constructivism asserts that it is necessary to find a mathematical object to prove that it exists. When one assumes that an object does not exist and derives a contradiction from that assumption, one still has not found the object and therefore not proved its...
, a pseudo-order is a constructive generalisation of a linear order to the continuous case. The usual trichotomy law does not hold in the constructive continuum because of its indecomposability
Indecomposability
In constructive mathematics, indecomposability or indivisibility is the principle that the continuum cannot be partitioned into two nonempty pieces. This principle was established by Brouwer in 1928 using intuitionistic principles, and can also be proven using Church's thesis...
, so this condition is weakened.
A pseudo-order is a binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
satisfying the following conditions:
- It is not possible for two elements to each be less than the other. That is,
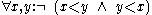 .
. - For all , , and , if then either or . That is,
 .
. - Every two elements for which neither one is less than the other must be equal. That is,
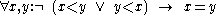
This first condition is simply asymmetry
Asymmetric relation
Asymmetric often means, simply: not symmetric. In this sense an asymmetric relation is a binary relation which is not a symmetric relation.That is,\lnot....
. It follows from the first two conditions that a pseudo-order is transitive
Transitive relation
In mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
. The second condition is often called co-transitivity or comparison and is the constructive substitute for trichotomy. In general, given two elements of a pseudo-ordered set, it is not always the case that either one is less than the other or else they are equal, but given any nontrivial interval, any element is either above the lower bound, or below the upper bound.
The third condition is often taken as the definition of equality. The natural apartness relation
Apartness relation
In constructive mathematics, an apartness relation is a constructive form of inequality, and is often taken to be more basic than equality. It is often written as # to distinguish from the negation of equality ≠, which is weaker....
on a pseudo-ordered set is given by
and equality is defined by the negation of apartness.
The negation of the pseudo-order is a partial order which is close to a total order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
: if x ≤ y is defined as the negation of y < x, then we have
Using classical logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
one would then conclude that x ≤ y or y ≤ x, so it would be a total order. However, this inference is not valid in the constructive case.
The prototypical pseudo-order is that of the real numbers: one real number is less than another if there exists (one can construct) a rational number greater than the former and less than the latter. In other words, x < y if there exists a rational number z such that x < z < y.