
Pseudogroup
Encyclopedia
In mathematics
, a pseudogroup is an extension of the group
concept, but one that grew out of the geometric approach of Sophus Lie
, rather than out of abstract algebra
(such as quasigroup
, for example). A theory of pseudogroups was developed by Élie Cartan
in the early 1900s.
It is not an axiomatic algebraic idea; rather it defines a set of closure conditions on sets of homeomorphism
s defined on open set
s U of a given Euclidean space
E or more generally of a fixed topological space
S. The groupoid
condition on those is fulfilled, in that homeomorphisms
and
compose to a homeomorphism from U to W. The further requirement on a pseudogroup is related to the possibility of patching (in the sense of descent
, transition function
s, or a gluing axiom
).
Specifically, a pseudogroup on a topological space S is a collection Γ of homeomorphisms between open subsets of S satisfying the following properties.
An example in space of two dimensions is the pseudogroup of invertible holomorphic function
s of a complex variable (invertible in the sense of having an inverse function
). The properties of this pseudogroup are what makes it possible to define Riemann surface
s by local data patched together.
In general, pseudogroups were studied as a possible theory of infinite dimensional Lie groups. The concept of a local Lie group, namely a pseudogroup of functions defined in neighbourhoods of the origin of E, is actually closer to Lie's original concept of Lie group
, in the case where the transformations involved depend on a finite number of parameter
s, than the contemporary definition via manifold
s. One of Cartan's achievements was to clarify the points involved, including the point that a local Lie group always gives rise to a global group, in the current sense (an analogue of Lie's third theorem
, on Lie algebra
s determining a group). The formal group
is yet another approach to the specification of Lie groups, infinitesimally. It is known, however, that local topological group
s do not necessarily have global counterparts.
Examples of infinite-dimensional pseudogroups abound, beginning with the pseudogroup of all diffeomorphism
s of E. The interest is mainly in sub-pseudogroups of the diffeomorphisms, and therefore with objects that have a Lie algebra analogue of vector field
s. Methods proposed by Lie and by Cartan for studying these objects have become more practical given the progress of computer algebra.
In the 1950s Cartan's theory was reformulated by Shiing-Shen Chern
, and a general deformation theory
for pseudogroups was developed by Kunihiko Kodaira and D. C. Spencer. In the 1960s homological algebra
was applied to the basic PDE
questions involved, of over-determination; this though revealed that the algebra of the theory is potentially very heavy. In the same decade the interest for theoretical physics
of infinite-dimensional Lie theory appeared for the first time, in the shape of current algebra
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a pseudogroup is an extension of the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
concept, but one that grew out of the geometric approach of Sophus Lie
Sophus Lie
Marius Sophus Lie was a Norwegian mathematician. He largely created the theory of continuous symmetry, and applied it to the study of geometry and differential equations.- Biography :...
, rather than out of abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
(such as quasigroup
Quasigroup
In mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...
, for example). A theory of pseudogroups was developed by Élie Cartan
Élie Cartan
Élie Joseph Cartan was an influential French mathematician, who did fundamental work in the theory of Lie groups and their geometric applications...
in the early 1900s.
It is not an axiomatic algebraic idea; rather it defines a set of closure conditions on sets of homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
s defined on open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s U of a given Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
E or more generally of a fixed topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
S. The groupoid
Groupoid
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
condition on those is fulfilled, in that homeomorphisms
- h:U → V
and
- g:V → W
compose to a homeomorphism from U to W. The further requirement on a pseudogroup is related to the possibility of patching (in the sense of descent
Descent (category theory)
In mathematics, the idea of descent has come to stand for a very general idea, extending the intuitive idea of 'gluing' in topology. Since the topologists' glue is actually the use of equivalence relations on topological spaces, the theory starts with some ideas on identification.A sophisticated...
, transition function
Transition function
In mathematics, a transition function has several different meanings:* In topology, a transition function is a homeomorphism from one coordinate chart to another...
s, or a gluing axiom
Gluing axiom
In mathematics, the gluing axiom is introduced to define what a sheaf F on a topological space X must satisfy, given that it is a presheaf, which is by definition a contravariant functor...
).
Specifically, a pseudogroup on a topological space S is a collection Γ of homeomorphisms between open subsets of S satisfying the following properties.
- For every open set U in S, the identity map on U is in Γ.
- If f is in Γ, then so is f −1.
- If f is in Γ, then the restriction of f to an arbitrary open subset of its domain is in Γ.
- If U is open in S, U is the union of the open sets { Ui }, f is a homeomorphism from U to an open subset of S, and the restriction of f to Ui is in Γ for all i, then f is in Γ.
- If f:U → V and f ′:U ′ → V ′ are in Γ, and the intersectionIntersectionIntersection has various meanings in different contexts:*In mathematics and geometry**Intersection , the set of elements common to some collection of sets.**Line-line intersection**Line-plane intersection**Line–sphere intersection...
V ∩ U ′ is not empty, then the following restricted composition is in Γ: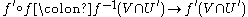 .
.
An example in space of two dimensions is the pseudogroup of invertible holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s of a complex variable (invertible in the sense of having an inverse function
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
). The properties of this pseudogroup are what makes it possible to define Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
s by local data patched together.
In general, pseudogroups were studied as a possible theory of infinite dimensional Lie groups. The concept of a local Lie group, namely a pseudogroup of functions defined in neighbourhoods of the origin of E, is actually closer to Lie's original concept of Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, in the case where the transformations involved depend on a finite number of parameter
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
s, than the contemporary definition via manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
s. One of Cartan's achievements was to clarify the points involved, including the point that a local Lie group always gives rise to a global group, in the current sense (an analogue of Lie's third theorem
Lie's third theorem
In mathematics, Lie's third theorem often means the result that states that any finite-dimensional Lie algebra g, over the real numbers, is the Lie algebra associated to some Lie group G. The relationship to the history has though become confused....
, on Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
s determining a group). The formal group
Formal group
In mathematics, a formal group law is a formal power series behaving as if it were the product of a Lie group. They were introduced by . The term formal group sometimes means the same as formal group law, and sometimes means one of several generalizations. Formal groups are intermediate between...
is yet another approach to the specification of Lie groups, infinitesimally. It is known, however, that local topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
s do not necessarily have global counterparts.
Examples of infinite-dimensional pseudogroups abound, beginning with the pseudogroup of all diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
s of E. The interest is mainly in sub-pseudogroups of the diffeomorphisms, and therefore with objects that have a Lie algebra analogue of vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s. Methods proposed by Lie and by Cartan for studying these objects have become more practical given the progress of computer algebra.
In the 1950s Cartan's theory was reformulated by Shiing-Shen Chern
Shiing-Shen Chern
Shiing-Shen Chern was a Chinese American mathematician, one of the leaders in differential geometry of the twentieth century.-Early years in China:...
, and a general deformation theory
Deformation theory
In mathematics, deformation theory is the study of infinitesimal conditions associated with varying a solution P of a problem to slightly different solutions Pε, where ε is a small number, or vector of small quantities. The infinitesimal conditions are therefore the result of applying the approach...
for pseudogroups was developed by Kunihiko Kodaira and D. C. Spencer. In the 1960s homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
was applied to the basic PDE
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
questions involved, of over-determination; this though revealed that the algebra of the theory is potentially very heavy. In the same decade the interest for theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
of infinite-dimensional Lie theory appeared for the first time, in the shape of current algebra
Current algebra
Current algebra is a mathematical framework in quantum field theory where the fields form a Lie algebra under their commutation relations.For instance, in a non-Abelian Yang–Mills symmetry, where ρ is the charge density,...
.

