
Pullback attractor
Encyclopedia
In mathematics
, the attractor of a random dynamical system
may be loosely thought of as a set to which the system evolves after a long enough time. The basic idea is the same as for a deterministic
dynamical system
, but requires careful treatment because random dynamical systems are necessarily non-autonomous. This requires one to consider the notion of a pullback attractor or attractor in the pullback sense.
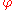 on a complete
on a complete
separable metric space
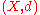 , where the noise is chosen from a probability space
, where the noise is chosen from a probability space
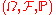 with base flow
with base flow
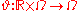 .
.
A naïve definition of an attractor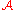 for this random dynamical system would be to require that for any initial condition
for this random dynamical system would be to require that for any initial condition 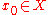 ,
, 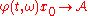 as
as  . This definition is far too limited, especially in dimension
. This definition is far too limited, especially in dimension
s higher than one. A more plausible definition, modelled on the idea of an omega-limit set
, would be to say that a point lies in the attractor
lies in the attractor 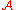 if and only if
if and only if
there exists an initial condition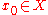 , there is a sequence of times
, there is a sequence of times  such that
such that
 as
as  .
.
This is not too far from a working definition. However, we have not yet considered the effect of the noise , which makes the system non-autonomous (i.e. it depends explicitly on time). For technical reasons, it becomes necessary to do the following: instead of looking
, which makes the system non-autonomous (i.e. it depends explicitly on time). For technical reasons, it becomes necessary to do the following: instead of looking  seconds into the "future", and considering the limit as
seconds into the "future", and considering the limit as  , one "rewinds" the noise
, one "rewinds" the noise  seconds into the "past", and evolves the system through
seconds into the "past", and evolves the system through  seconds using the same initial condition. That is, one is interested in the pullback limit
seconds using the same initial condition. That is, one is interested in the pullback limit
 .
.
So, for example, in the pullback sense, the omega-limit set for a (possibly random) set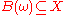 is the random set
is the random set
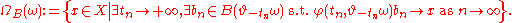
Equivalently, this may be written as
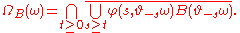
Importantly, in the case of a deterministic dynamical system (one without noise), the pullback limit coincides with the deterministic forward limit, so it is meaningful to compare deterministic and random omega-limit sets, attractors, and so forth.
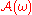 for a random dynamical system is a
for a random dynamical system is a  -almost surely
-almost surely
unique random set such that
There is a slight abuse of notation
in the above: the first use of "dist" refers to the Hausdorff semi-distance
from a point to a set,
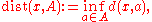
whereas the second use of "dist" refers to the Hausdorff semi-distance between two sets,
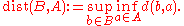
As noted in the previous section, in the absence of noise, this definition of attractor coincides with the deterministic definition of the attractor as the minimal compact invariant set that attracts all bounded deterministic sets.
 , then the random global attractor is given by
, then the random global attractor is given by
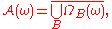
where the union is taken over all bounded sets .
.
 is ergodic and
is ergodic and  is a deterministic compact set with
is a deterministic compact set with

then
 -almost surely.
-almost surely.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the attractor of a random dynamical system
Random dynamical system
In mathematics, a random dynamical system is a measure-theoretic formulation of a dynamical system with an element of "randomness", such as the dynamics of solutions to a stochastic differential equation...
may be loosely thought of as a set to which the system evolves after a long enough time. The basic idea is the same as for a deterministic
Deterministic system (mathematics)
In mathematics, a deterministic system is a system in which no randomness is involved in the development of future states of the system. A deterministic model will thus always produce the same output from a given starting condition or initial state.-Examples:...
dynamical system
Dynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
, but requires careful treatment because random dynamical systems are necessarily non-autonomous. This requires one to consider the notion of a pullback attractor or attractor in the pullback sense.
Set-up and motivation
Consider a random dynamical system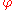 on a complete
on a completeComplete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
separable metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
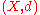 , where the noise is chosen from a probability space
, where the noise is chosen from a probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
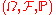 with base flow
with base flowBase flow
The term base flow may refer to* Baseflow in hydrology;* Base flow in the study of random dynamical systems in mathematics....
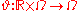 .
.A naïve definition of an attractor
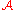 for this random dynamical system would be to require that for any initial condition
for this random dynamical system would be to require that for any initial condition 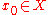 ,
, 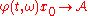 as
as  . This definition is far too limited, especially in dimension
. This definition is far too limited, especially in dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s higher than one. A more plausible definition, modelled on the idea of an omega-limit set
Limit set
In mathematics, especially in the study of dynamical systems, a limit set is the state a dynamical system reaches after an infinite amount of time has passed, by either going forward or backwards in time...
, would be to say that a point
 lies in the attractor
lies in the attractor 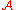 if and only if
if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
there exists an initial condition
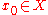 , there is a sequence of times
, there is a sequence of times  such that
such that as
as  .
.This is not too far from a working definition. However, we have not yet considered the effect of the noise
 , which makes the system non-autonomous (i.e. it depends explicitly on time). For technical reasons, it becomes necessary to do the following: instead of looking
, which makes the system non-autonomous (i.e. it depends explicitly on time). For technical reasons, it becomes necessary to do the following: instead of looking  seconds into the "future", and considering the limit as
seconds into the "future", and considering the limit as  , one "rewinds" the noise
, one "rewinds" the noise  seconds into the "past", and evolves the system through
seconds into the "past", and evolves the system through  seconds using the same initial condition. That is, one is interested in the pullback limit
seconds using the same initial condition. That is, one is interested in the pullback limit .
.So, for example, in the pullback sense, the omega-limit set for a (possibly random) set
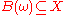 is the random set
is the random set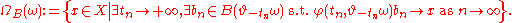
Equivalently, this may be written as
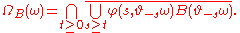
Importantly, in the case of a deterministic dynamical system (one without noise), the pullback limit coincides with the deterministic forward limit, so it is meaningful to compare deterministic and random omega-limit sets, attractors, and so forth.
Definition
The pullback attractor (or random global attractor)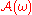 for a random dynamical system is a
for a random dynamical system is a  -almost surely
-almost surelyAlmost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
unique random set such that
-
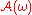 is a random compact setRandom compact setIn mathematics, a random compact set is essentially a compact set-valued random variable. Random compact sets are useful in the study of attractors for random dynamical systems.-Definition:...
is a random compact setRandom compact setIn mathematics, a random compact set is essentially a compact set-valued random variable. Random compact sets are useful in the study of attractors for random dynamical systems.-Definition:...
: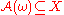 is almost surely compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
is almost surely compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and is a
is a 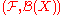 -measurable functionMeasurable functionIn mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
-measurable functionMeasurable functionIn mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
for every ;
; -
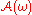 is invariant: for all
is invariant: for all 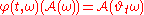 almost surely;
almost surely; -
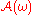 is attractive: for any deterministic bounded setBounded setIn mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
is attractive: for any deterministic bounded setBounded setIn mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
 ,
,
-
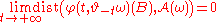 almost surely.
almost surely.
There is a slight abuse of notation
Abuse of notation
In mathematics, abuse of notation occurs when an author uses a mathematical notation in a way that is not formally correct but that seems likely to simplify the exposition or suggest the correct intuition . Abuse of notation should be contrasted with misuse of notation, which should be avoided...
in the above: the first use of "dist" refers to the Hausdorff semi-distance
Hausdorff distance
In mathematics, the Hausdorff distance, or Hausdorff metric, also called Pompeiu–Hausdorff distance, measures how far two subsets of a metric space are from each other. It turns the set of non-empty compact subsets of a metric space into a metric space in its own right...
from a point to a set,
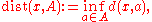
whereas the second use of "dist" refers to the Hausdorff semi-distance between two sets,
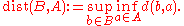
As noted in the previous section, in the absence of noise, this definition of attractor coincides with the deterministic definition of the attractor as the minimal compact invariant set that attracts all bounded deterministic sets.
The attractor as a union of omega-limit sets
If a random dynamical system has a compact random absorbing setAbsorbing set (random dynamical systems)
In mathematics, an absorbing set for a random dynamical system is a subset of the phase space that eventually contains the image of any bounded set under the cocycle of the random dynamical system...
 , then the random global attractor is given by
, then the random global attractor is given by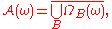
where the union is taken over all bounded sets
 .
.Bounding the attractor within a deterministic set
Crauel (1999) proved that if the base flow is ergodic and
is ergodic and  is a deterministic compact set with
is a deterministic compact set with
then

 -almost surely.
-almost surely.

