Pyritohedron
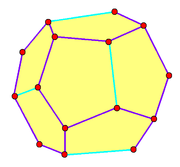A pyritohedron has 30 edges, divided into two lengths: 24 and 6 in each group.
Face polygon	irregular pentagon Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
Faces Face (geometry) In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...	12
Edges Edge (geometry) In geometry, an edge is a one-dimensional line segment joining two adjacent zero-dimensional vertices in a polygon. Thus applied, an edge is a connector for a one-dimensional line segment and two zero-dimensional objects....	30 (6+24)
Vertices Vertex (geometry) In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...	20 (8+12)
Symmetry group	Th, [4,3+], (3*2)
Dual polyhedron Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...	Pseudoicosahedron Pseudoicosahedron In geometry, a pseudoicosahedron is a twelve-sided polyhedron that can be regarded as a particular form of distorted regular icosahedron containing tetrahedral symmetry...
Properties	convex Convex set In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...

In geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, a pyritohedron is an irregular dodecahedron with pyritohedral (T_h) symmetry. Like the regular dodecahedron, it has twelve identical pentagon

Pentagon

In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...

al faces, with three meeting in each of the 20 vertices. However, the pentagons are not regular, and the structure has no fivefold symmetry axes. Its 30 edges are divided into two sets - containing 24 and 6 edges of the same length.

Although regular dodecahedra do not exist in crystals, the distorted pyritohedron form occurs in the crystal pyrite, and it may be an inspiration for the discovery of the regular Platonic solid

Platonic solid

In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...

 form.

Crystal pyrite

Its name comes from one of the two common crystal forms of pyrite

Pyrite

The mineral pyrite, or iron pyrite, is an iron sulfide with the formula FeS2. This mineral's metallic luster and pale-to-normal, brass-yellow hue have earned it the nickname fool's gold because of its resemblance to gold...

, the other one being cubical.

Cubic pyrite

Pyritohedral

Ho-Mg-Zn quasicrystal

Cartesian coordinates

The coordinates of the 8 vertices:

(±1, ±1, ±1)

The coordinates of the 12 vertices are the permutations of:

(0, 1+h, 1−h²)

where h is the height of the wedge

Wedge (geometry)

In solid geometry, a wedge is a polyhedron defined by two triangles and three trapezoid faces. A wedge has five faces, nine edges, and six vertices.A wedge is a subclass of the prismatoids with the base and opposite ridge in two parallel planes....

 roof above the faces of the cube. When h=1, the 6 edges degenerate to points and rhombic dodecahedron

Rhombic dodecahedron

In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:...

 is formed. For the regular dodecahedron, h=(√5−1)/2, the golden ratio

Golden ratio

In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...

.

Geometric freedom

The pyritohedron has a geometric degree of freedom with limiting cases of a cubic convex hull

Convex hull

In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....

 at one limit of colinear edges, and a rhombic dodecahedron

Rhombic dodecahedron

In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:...

 as the other limit as 6 edges are degenerated to length zero. The regular dodecahedron represents a special intermediate case where all edges and angles are equal.

Special cases of the pyritohedron

2 : 1	1.3092... : 1	1 : 1	0 : 1
A cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...  can be divided into a pyritohedron by bisecting all the edges, and faces in alternate directions.	The geometric proportions of the pyritohedron in the Weaire–Phelan structure	A regular dodecahedron is an intermediate case with equal edge lengths.	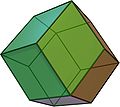A rhombic dodecahedron Rhombic dodecahedron In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:...  is the limiting case with the 6 crossedges reducing to length zero.

A regular dodecahedron can be formed from a cube in the following way: The top square in the cube is replaced by a "roof" composed of two pentagons, joined along the top of the roof. The diagonals in the pentagons parallel to the top of the roof coincide with two opposite sides of the square. The other five squares are replaced by a pair of pentagons in a similar way. The pyritohedron is constructed by changing the slope of these "roofs".

Concave forms

An example concave pyritohedral dodecahedron

External links

• Stellation of Pyritohedron VRML models and animations of Pyritohedron and its stellation
  Stellation
  Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
  
  s.
• Plato's Fourth Solid and the "Pyritohedron", by Paul Stephenson, 1993, The Mathematical Gazette, Vol. 77, No. 479 (Jul., 1993), pp. 220–226 http://www.jstor.org/pss/3619718
• THE GREEK ELEMENTS