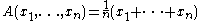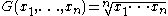In mathematics, the three classical Pythagorean means are the arithmetic mean

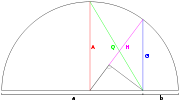
Arithmetic mean

In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...

 (A), the geometric mean

Geometric mean

The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...

 (G), and the harmonic mean

Harmonic mean

In mathematics, the harmonic mean is one of several kinds of average. Typically, it is appropriate for situations when the average of rates is desired....

 (H). They are defined by:

• 
• 
• 

Each mean has the following properties:

• Value preservation:
• First order homogeneity
  Homogeneous function
  In mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
  
  :
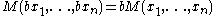
• Invariance under exchange: for any and .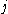
• Averaging:

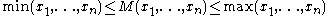
These means were studied with proportions by Pythagoreans and later generations of Greek mathematicians (Thomas Heath, History of Ancient Greek Mathematics) because of their importance in geometry and music.

There is an ordering to these means (if all of the 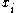are positive), along with the quadratic mean :

with equality holding if and only if the 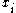are all equal. This is a generalization of the inequality of arithmetic and geometric means

Inequality of arithmetic and geometric means

In mathematics, the inequality of arithmetic and geometric means, or more briefly the AM–GM inequality, states that the arithmetic mean of a list of non-negative real numbers is greater than or equal to the geometric mean of the same list; and further, that the two means are equal if and only if...

 and a special case of an inequality for generalized mean

Generalized mean

In mathematics, a generalized mean, also known as power mean or Hölder mean , is an abstraction of the Pythagorean means including arithmetic, geometric, and harmonic means.-Definition:...

s. This inequality sequence can be proved for the 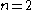case for the numbers a and b using a sequence of right triangle

Right triangle

A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...

s (x, y, z) with hypotenuse

Hypotenuse

In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...

 z and the Pythagorean theorem

Pythagorean theorem

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...

, which states that 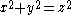and implies that 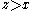and 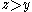. The right triangles are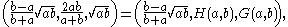


showing that ;


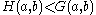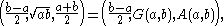
showing that ;

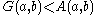and


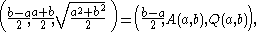
showing that .

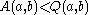External links

• Pythagorean means on MathWorld