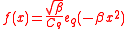Q-Gaussian distribution
Encyclopedia
In q-analog
theory, the q-Gaussian is a probability distribution arising from the maximization of the Tsallis entropy
under appropriate constraints. It is one example of a Tsallis distribution
. The q-Gaussian is a generalization of the Gaussian in the same way that Tsallis entropy is a generalization of standard Boltzmann–Gibbs entropy or Shannon entropy. The normal distribution is recovered as
.
The q-Gaussian has been applied to problems in the fields of statistical mechanics
, geology
, anatomy
, astronomy
, economics
, finance
, and machine learning
. The distribution is often favored for its heavy tails in comparison to the Gaussian for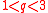
. There is generalized q-analog
of the classical central limit theorem
in which the independence constraint for the i.i.d. variables
is relaxed to an extent defined by the q parameter, with independence being recovered as q → 1. In analogy to the classical central limit theorem, san average of such random variables with fixed mean and variance tend towards the q-Gaussian distribution.
In the heavy tail regions, the distribution is equivalent to the Student's t-distribution with a direct mapping between q and the degrees of freedom
. A practioner using one of these distributions can therefore parameterize the same distribution in two different ways. The choice of the q-Gaussian form may arise if the system is non-extensive
, or if there is lack of a connection to small samples sizes.
where
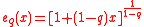
is the q-exponential and the normalization factor
is given by
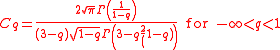
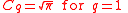
distribution for fixed values of the first moment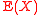
and second moment 
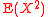(with the fixed zeroth moment 
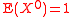corresponding to the normalization condition), the q-Gaussian distribution is the maximum Tsallis entropy
distribution for fixed values of these three moments.
was constrained to be a positive integer related to the sample size, but it is readily observed that Gosset's density function is valid for all real values of 
. The scaled reparametrization introduces the alternative parameters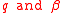 
which are related to 
.
Given a Student T distribution with
degrees of freedom, the equivalent q-Gaussian is
with inverse
Whenever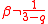
, the function is simply a scaled version of the Student T.
It is sometimes argued that the distribution is a generalization of the Student to negative and or non-integer degrees of freedom. However, the theory of the Student extends trivially to all real degrees of freedom, where the support of the distribution is now compact
rather than infinite in the case of
. The formula for the T-density function is given in many standard texts and it is a simple matter to confirm the above formulae. The best starting point is Gosset's original work, discussed in the article on William Sealy Gosset
.
. The density then becomes defined by
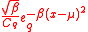
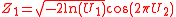
The generalized Box–Muller technique can generates pairs of q-gaussian deviates that are not independent. In practice, only a single deviate will be generated from a pair of uniformly distributed variables. The following formula will generate deviates from a q-Gaussian with specified parameter q and
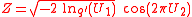
Where
is the q-logarithm and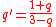 
These deviates can be transformed to generate deviates from an arbitrary q-Gaussian by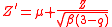
Q-analog
Roughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...
theory, the q-Gaussian is a probability distribution arising from the maximization of the Tsallis entropy
Tsallis entropy
In physics, the Tsallis entropy is a generalization of the standard Boltzmann-Gibbs entropy. In the scientific literature, the physical relevance of the Tsallis entropy is highly debated...
under appropriate constraints. It is one example of a Tsallis distribution
Tsallis distribution
In q-analog theory and statistical mechanics, a Tsallis distribution is a probability distribution derived from the maximization of the Tsallis entropy under appropriate constraints. There are several different families of Tsallis distributions, yet different sources may reference an individual...
. The q-Gaussian is a generalization of the Gaussian in the same way that Tsallis entropy is a generalization of standard Boltzmann–Gibbs entropy or Shannon entropy. The normal distribution is recovered as
.The q-Gaussian has been applied to problems in the fields of statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, geology
Geology
Geology is the science comprising the study of solid Earth, the rocks of which it is composed, and the processes by which it evolves. Geology gives insight into the history of the Earth, as it provides the primary evidence for plate tectonics, the evolutionary history of life, and past climates...
, anatomy
Anatomy
Anatomy is a branch of biology and medicine that is the consideration of the structure of living things. It is a general term that includes human anatomy, animal anatomy , and plant anatomy...
, astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
, economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
, finance
Finance
"Finance" is often defined simply as the management of money or “funds” management Modern finance, however, is a family of business activity that includes the origination, marketing, and management of cash and money surrogates through a variety of capital accounts, instruments, and markets created...
, and machine learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
. The distribution is often favored for its heavy tails in comparison to the Gaussian for
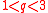. There is generalized q-analogQ-analog
Roughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...
of the classical central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
in which the independence constraint for the i.i.d. variables
Independent and identically distributed random variables
In probability theory and statistics, a sequence or other collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent....
is relaxed to an extent defined by the q parameter, with independence being recovered as q → 1. In analogy to the classical central limit theorem, san average of such random variables with fixed mean and variance tend towards the q-Gaussian distribution.
In the heavy tail regions, the distribution is equivalent to the Student's t-distribution with a direct mapping between q and the degrees of freedom
Degrees of freedom
Degrees of freedom can mean:* Degrees of freedom , independent displacements and/or rotations that specify the orientation of the body or system...
. A practioner using one of these distributions can therefore parameterize the same distribution in two different ways. The choice of the q-Gaussian form may arise if the system is non-extensive
Nonextensive entropy
Entropy is considered to be an extensive property, i.e., that its value depends on the amount of material present. Constantino Tsallis has proposed a nonextensive entropy, which is a generalization of the traditional Boltzmann-Gibbs entropy....
, or if there is lack of a connection to small samples sizes.
Probability density function
The q-Gaussian has the probability density function
where
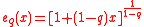
is the q-exponential and the normalization factor
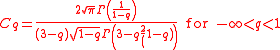
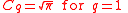
is given byEntropy
Just as the normal distribution is the maximum information entropyInformation entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
distribution for fixed values of the first moment
and second moment 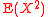(with the fixed zeroth moment 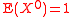corresponding to the normalization condition), the q-Gaussian distribution is the maximum Tsallis entropyTsallis entropy
In physics, the Tsallis entropy is a generalization of the standard Boltzmann-Gibbs entropy. In the scientific literature, the physical relevance of the Tsallis entropy is highly debated...
distribution for fixed values of these three moments.
Student's t-distribution
While it can be justified by an interesting alternative form of entropy, statistically it is a scaled reparametrization of the Student's t-distribution introduced by W. Gosset in 1908 to describe small-sample statistics. In Gosset's original presentation the degrees of freedom parameter was constrained to be a positive integer related to the sample size, but it is readily observed that Gosset's density function is valid for all real values of . The scaled reparametrization introduces the alternative parameters 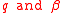which are related to .Given a Student T distribution with
degrees of freedom, the equivalent q-Gaussian iswith inverse
Whenever
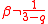, the function is simply a scaled version of the Student T.It is sometimes argued that the distribution is a generalization of the Student to negative and or non-integer degrees of freedom. However, the theory of the Student extends trivially to all real degrees of freedom, where the support of the distribution is now compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
rather than infinite in the case of
. The formula for the T-density function is given in many standard texts and it is a simple matter to confirm the above formulae. The best starting point is Gosset's original work, discussed in the article on William Sealy GossetWilliam Sealy Gosset
William Sealy Gosset is famous as a statistician, best known by his pen name Student and for his work on Student's t-distribution....
.
Three-parameter version
As with many distributions centered around zero, the q-gaussian can be trivially extended to include a location parameter. The density then becomes defined by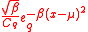Generating random deviates
The Box–Muller transform has been generalized to allow random sampling from q-gaussians. The standard Box–Muller technique generates pairs of independent normally distributed variables from equations of the following form.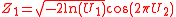The generalized Box–Muller technique can generates pairs of q-gaussian deviates that are not independent. In practice, only a single deviate will be generated from a pair of uniformly distributed variables. The following formula will generate deviates from a q-Gaussian with specified parameter q and
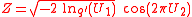
Where
is the q-logarithm and 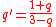These deviates can be transformed to generate deviates from an arbitrary q-Gaussian by
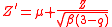
Physics
It has been shown that the momentum distribution of cold atoms in dissipative optical lattices is a q-GaussianFinance
Financial return distributions in the New York Stock Exchange, NASDAQ and elsewhere are often interpreted as q-Gaussians.See also
- Constantino TsallisConstantino TsallisConstantino Tsallis is a naturalized Brazilian physicist working in Rio de Janeiro at CBPF, Brazil. He was born in Greece, and grew up in Argentina, where he studied physics at Instituto Balseiro, in Bariloche. In 1974 he received a Doctorat d'Etat et Sciences Physiques degree from the University...
- Tsallis statisticsTsallis statisticsThe term Tsallis statistics usually refers to the collection of q-analogs of mathematical functions and associated probability distributions that were originated by Constantino Tsallis. Using these tools, it is possible to derive Tsallis distributions from the optimization of the Tsallis entropic...
- Tsallis entropyTsallis entropyIn physics, the Tsallis entropy is a generalization of the standard Boltzmann-Gibbs entropy. In the scientific literature, the physical relevance of the Tsallis entropy is highly debated...
- Tsallis distributionTsallis distributionIn q-analog theory and statistical mechanics, a Tsallis distribution is a probability distribution derived from the maximization of the Tsallis entropy under appropriate constraints. There are several different families of Tsallis distributions, yet different sources may reference an individual...
- q-exponential distribution
Further reading
- Juniper, J. (2007) "The Tsallis Distribution and Generalised Entropy: Prospects for Future Research into Decision-Making under Uncertainty", Centre of Full Employment and Equity, The University of Newcastle, Australia