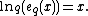Tsallis statistics
Encyclopedia
The term Tsallis statistics usually refers to the collection of q-analog
s of mathematical functions and associated probability distributions that were originated by Constantino Tsallis
. Using these tools, it is possible to derive Tsallis distribution
s from the optimization of the Tsallis entropic form
. A continuous real parameter q can be used to adjust the distributions so that distributions which have properties intermediate to that of Gaussian and Lévy distributions can be created. This parameter q represents the degree of non-extensivity of the distribution. Tsallis statistics are useful for characterising complex, anomalous diffusion
.
function using the parameter q.

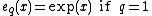
Note that the q-exponential in Tsallis statistics is different from a version used elsewhere.
using the parameter q.
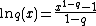

These functions have the property that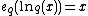
and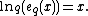
Q-analog
Roughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...
s of mathematical functions and associated probability distributions that were originated by Constantino Tsallis
Constantino Tsallis
Constantino Tsallis is a naturalized Brazilian physicist working in Rio de Janeiro at CBPF, Brazil. He was born in Greece, and grew up in Argentina, where he studied physics at Instituto Balseiro, in Bariloche. In 1974 he received a Doctorat d'Etat et Sciences Physiques degree from the University...
. Using these tools, it is possible to derive Tsallis distribution
Tsallis distribution
In q-analog theory and statistical mechanics, a Tsallis distribution is a probability distribution derived from the maximization of the Tsallis entropy under appropriate constraints. There are several different families of Tsallis distributions, yet different sources may reference an individual...
s from the optimization of the Tsallis entropic form
Tsallis entropy
In physics, the Tsallis entropy is a generalization of the standard Boltzmann-Gibbs entropy. In the scientific literature, the physical relevance of the Tsallis entropy is highly debated...
. A continuous real parameter q can be used to adjust the distributions so that distributions which have properties intermediate to that of Gaussian and Lévy distributions can be created. This parameter q represents the degree of non-extensivity of the distribution. Tsallis statistics are useful for characterising complex, anomalous diffusion
Anomalous Diffusion
Anomalous diffusion is a term used to describe a diffusion process with a non-linear relationship to time, in contrast to a typical diffusion process, in which the mean squared displacement , σr2, of a particle is a linear function of time....
.
Tsallis functions
The q-deformed exponential and logarithmic functions where first introduced in Tsallis statistics in 1994q-exponential
The q-exponential is a deformation of the exponentialExponential
Exponential may refer to any of several mathematical topics related to exponentiation, including:*Exponential function, also:**Matrix exponential, the matrix analogue to the above*Exponential decay, decrease at a rate proportional to value...
function using the parameter q.

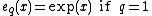
Note that the q-exponential in Tsallis statistics is different from a version used elsewhere.
q-logarithm
The q-logartihm is the inverse of q-exponential and a deformation of the logarithmLogarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
using the parameter q.
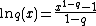

These functions have the property that
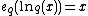
and