Quantum amplifier
Encyclopedia
A quantum amplifer is an amplifier
that uses quantum mechanical
methods to amplify a quantum signal; examples include the active elements of optical lasers and optical re-transmitters.
The main properties of the quantum amplifier are its amplification coefficient and uncertainty
. These parameters are not independent; the higher the amplification coefficient, the higher the noise. In the case of lasers, the uncertainty corresponds to the amplified spontaneous emission
of the active medium. The unavoidable noise of quantum amplifiers is one of the reasons for the use of digital signal
s in optical communications and can be deduced from the fundamentals of quantum mechanics
.
increases the amplitude of whatever goes through it. While classical amplifiers take in classical signals, quantum amplifiers take in quantum signals like coherent state
s. This does not mean that the output is a coherent state; optical quantum amplifiers with feedback are examples. Besides amplifying the intensity of the input, quantum amplifiers increase the uncertainty
of the signal, unlike a classical amplifier.
The physical electric field in a paraxial single-mode pulse can be approximated with superposition
of modes; the partial field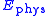
of such a mode can be described with
where
The amplitude of field in this mode must be able to be detected. All the quantum-mechanical analysis of the noise is about the mean value of the annihilation operator and its uncertainty; the technical problems with detection of the real and imaginary parts of the projection of the field to a given mode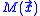
must be solved. Therefore, spatial coordinates do not appear in the deduction, and symbols 
may be used for Hermitian and anti-Hermitian parts of the annihilation operator.
Assume that the mean value of the initial field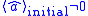
. Physically, in terms of a laser, the initial state may correspond to the coherent pulse at the input of the optical amplifier, and the final state may correspond to the output pulse. The amplitude-phase behavior of the pulse must be known, and only the quantum state of the corresponding mode is important. In this case, the pulse may be treated in terms of a single-mode field.
Hence, a quantum amplifier is a unitary transform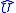
, which converts the input quantum state
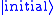to the amplified state 
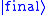. This is the quantum amplifier in the wave function representation.
The amplification may change as the mean value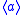
of the field operator 
and its dispersion 
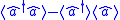change. The coherent state represents the minimum uncertainty; as the state is transformed, the uncertainty may increase. This increase can be interpreted as noise in the amplifier.
The transformation of state can be written as follows:
The coefficient
of amplification can be defined as follows:
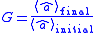
This expression can be written also in the matrix
representation; all the changes may be attributed to the amplification to the operator of field, and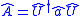
may be assumed, keeping the vector of state unchanged. Then:
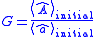
In general, the coefficient
may be complex, and it may depend on the initial state. For application to lasers, the amplification of coherent state
s are important. Therefore, it is usually assumed that the initial state is a coherent state characterized with a complex initial parameter
such that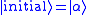 
. Even after such a restriction, the coefficient of amplification may depend on the amplitude or phase of the initial field. In the following consideration, only the matrix representation is used; all the brackets are assumed to be evaluated with respect to the initial coherent state.
The noise of the amplifier can be defined as follows:
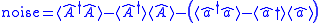
This quantity characterizes the increase of uncertainty of the field due to amplification. As the uncertainty of the field operator at the coherent state does not depend on its parameter, the quantity above shows how different from the coherent state is the output field.
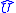amplifies in such a way that the input 
and the output 
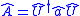are related by a linear equation
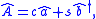
where
and 
are c-number
s and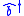
is an operator in the amplifier. Without loss of generality, it may be assumed that 
and 
are real
. The unitary transformation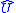
preserves the commutator of the field operators, so:
From the unitarity of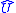
, it follows that 
satisfies the standard commutation relation for the Bose operators
and
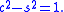
Hence, the amplifier is equivalent to an additional mode of the field with a large amount of energy stored, and behaves as a boson
. Calculating the gain and the noise of this amplifier, we get
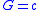
and
The coefficient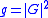
should be interpreted as the intensity amplification coefficient, and the noise of the linear amplifier as 
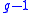. The gain can be dropped out by the splitting of the beam; therefore, the estimate above is the minimal noise of the linear quantum amplifier.
The linear amplifier has an advantage over the multi-mode amplifier because if several modes of a linear amplifier are amplified by the same factor, the noise in each mode is determined independently; modes in a linear quantum amplifier are independent.
For a large amplification coefficient, the minimal noise can be realized with homodyne detection and construction of a field state with known amplitude and phase, which corresponds to the linear phase-invariant amplifier. The uncertainty principle
sets the lower bound of quantum noise
in an amplifier. In particular, the output of a laser system and the output of an optical generator are not coherent states.
s of the mapping function; a larger derivative implies an amplifier with greater uncertainty. Examples include most lasers, which include near-linear amplifiers, operate close to their threshold and thus exhibit large uncertainty and nonlinear operation. As with the linear amplifiers, they may preserve the phase and keep the uncertainty low, but there are exceptions. These include parametric oscillator
s, which amplify while shifting the phase of the input.
Amplifier
Generally, an amplifier or simply amp, is a device for increasing the power of a signal.In popular use, the term usually describes an electronic amplifier, in which the input "signal" is usually a voltage or a current. In audio applications, amplifiers drive the loudspeakers used in PA systems to...
that uses quantum mechanical
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
methods to amplify a quantum signal; examples include the active elements of optical lasers and optical re-transmitters.
The main properties of the quantum amplifier are its amplification coefficient and uncertainty
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
. These parameters are not independent; the higher the amplification coefficient, the higher the noise. In the case of lasers, the uncertainty corresponds to the amplified spontaneous emission
Amplified spontaneous emission
Amplified spontaneous emission or superluminescence is light, produced by spontaneous emission, that has been optically amplified by the process of stimulated emission in a gain medium. It is inherent in the field of random lasers....
of the active medium. The unavoidable noise of quantum amplifiers is one of the reasons for the use of digital signal
Digital signal
A digital signal is a physical signal that is a representation of a sequence of discrete values , for example of an arbitrary bit stream, or of a digitized analog signal...
s in optical communications and can be deduced from the fundamentals of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
Introduction
An amplifierAmplifier
Generally, an amplifier or simply amp, is a device for increasing the power of a signal.In popular use, the term usually describes an electronic amplifier, in which the input "signal" is usually a voltage or a current. In audio applications, amplifiers drive the loudspeakers used in PA systems to...
increases the amplitude of whatever goes through it. While classical amplifiers take in classical signals, quantum amplifiers take in quantum signals like coherent state
Coherent state
In quantum mechanics a coherent state is a specific kind of quantum state of the quantum harmonic oscillator whose dynamics most closely resembles the oscillating behaviour of a classical harmonic oscillator...
s. This does not mean that the output is a coherent state; optical quantum amplifiers with feedback are examples. Besides amplifying the intensity of the input, quantum amplifiers increase the uncertainty
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
of the signal, unlike a classical amplifier.
The physical electric field in a paraxial single-mode pulse can be approximated with superposition
Quantum superposition
Quantum superposition is a fundamental principle of quantum mechanics. It holds that a physical system exists in all its particular, theoretically possible states simultaneously; but, when measured, it gives a result corresponding to only one of the possible configurations.Mathematically, it...
of modes; the partial field
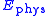of such a mode can be described withwhere
is vector of spatial coordinates,
is the vector of polarization of the pulse,
is wavevector,
is the operator of annihilation of photon in some specific mode 
.
The amplitude of field in this mode must be able to be detected. All the quantum-mechanical analysis of the noise is about the mean value of the annihilation operator and its uncertainty; the technical problems with detection of the real and imaginary parts of the projection of the field to a given mode
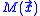must be solved. Therefore, spatial coordinates do not appear in the deduction, and symbols may be used for Hermitian and anti-Hermitian parts of the annihilation operator.Assume that the mean value of the initial field
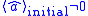. Physically, in terms of a laser, the initial state may correspond to the coherent pulse at the input of the optical amplifier, and the final state may correspond to the output pulse. The amplitude-phase behavior of the pulse must be known, and only the quantum state of the corresponding mode is important. In this case, the pulse may be treated in terms of a single-mode field.Hence, a quantum amplifier is a unitary transform
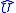, which converts the input quantum state 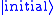to the amplified state 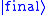. This is the quantum amplifier in the wave function representation.The amplification may change as the mean value
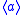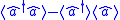of the field operator and its dispersion change. The coherent state represents the minimum uncertainty; as the state is transformed, the uncertainty may increase. This increase can be interpreted as noise in the amplifier.The transformation of state can be written as follows:
The coefficient
of amplification can be defined as follows: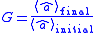This expression can be written also in the matrix
Matrix mechanics
Matrix mechanics is a formulation of quantum mechanics created by Werner Heisenberg, Max Born, and Pascual Jordan in 1925.Matrix mechanics was the first conceptually autonomous and logically consistent formulation of quantum mechanics. It extended the Bohr Model by describing how the quantum jumps...
representation; all the changes may be attributed to the amplification to the operator of field, and
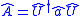may be assumed, keeping the vector of state unchanged. Then: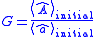In general, the coefficient
may be complex, and it may depend on the initial state. For application to lasers, the amplification of coherent stateCoherent state
In quantum mechanics a coherent state is a specific kind of quantum state of the quantum harmonic oscillator whose dynamics most closely resembles the oscillating behaviour of a classical harmonic oscillator...
s are important. Therefore, it is usually assumed that the initial state is a coherent state characterized with a complex initial parameter
such that 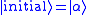. Even after such a restriction, the coefficient of amplification may depend on the amplitude or phase of the initial field. In the following consideration, only the matrix representation is used; all the brackets are assumed to be evaluated with respect to the initial coherent state.The noise of the amplifier can be defined as follows:
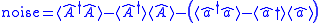
This quantity characterizes the increase of uncertainty of the field due to amplification. As the uncertainty of the field operator at the coherent state does not depend on its parameter, the quantity above shows how different from the coherent state is the output field.
Linear phase-invariant amplifiers
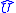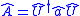Linear phase-invariant amplifiers are mathematical abstractions: assume that the unitary operator amplifies in such a way that the input and the output are related by a linear equation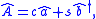where
and are c-numberC-number
The term c-number is an old nomenclature used by Paul Dirac which refers to real and complex numbers. It is used to distinguish from operators in quantum mechanics....
s and
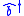is an operator in the amplifier. Without loss of generality, it may be assumed that and are realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
. The unitary transformation
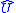preserves the commutator of the field operators, so:From the unitarity of
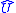, it follows that satisfies the standard commutation relation for the Bose operatorsand
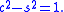
Hence, the amplifier is equivalent to an additional mode of the field with a large amount of energy stored, and behaves as a boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
. Calculating the gain and the noise of this amplifier, we get
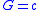
and
The coefficient
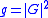should be interpreted as the intensity amplification coefficient, and the noise of the linear amplifier as 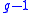. The gain can be dropped out by the splitting of the beam; therefore, the estimate above is the minimal noise of the linear quantum amplifier.The linear amplifier has an advantage over the multi-mode amplifier because if several modes of a linear amplifier are amplified by the same factor, the noise in each mode is determined independently; modes in a linear quantum amplifier are independent.
For a large amplification coefficient, the minimal noise can be realized with homodyne detection and construction of a field state with known amplitude and phase, which corresponds to the linear phase-invariant amplifier. The uncertainty principle
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
sets the lower bound of quantum noise
Quantum noise
Quantum noise is uncertainty of some physical quantity due to its quantum origin.In the case of number of particles , the quantum noise is also called shot noise. Most optical communications use amplitude modulation...
in an amplifier. In particular, the output of a laser system and the output of an optical generator are not coherent states.
Nonlinear amplifiers
Nonlinear amplifiers do not have a linear relation between their input and output; the maximum noise of a nonlinear amplifier cannot be much smaller than that of an idealized linear amplifier. This limit is determined by the derivativeDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s of the mapping function; a larger derivative implies an amplifier with greater uncertainty. Examples include most lasers, which include near-linear amplifiers, operate close to their threshold and thus exhibit large uncertainty and nonlinear operation. As with the linear amplifiers, they may preserve the phase and keep the uncertainty low, but there are exceptions. These include parametric oscillator
Parametric oscillator
A parametric oscillator is a harmonic oscillator whose parameters oscillate in time. For example, a well known parametric oscillator is a child pumping a swing by periodically standing and squatting to increase the size of the swing's oscillations. The varying of the parameters drives the system...
s, which amplify while shifting the phase of the input.
See also
- M. S. Kim, K. S. Lee, and V. Bužek. Amplification of superposition states in phase-sensitive amplifiers. Phys. Rev. A 47, 4302 (1993)
- R. S. Bondurant. Quantum noise properties of a nonlinear amplifier. Phys. Rev. Lett. 71, 1709 (1993)
- Yi Mu and C. M. Savage. Phase-sensitive above-threshold laser amplifiers. Phys. Rev. A 49, 4093 (1994)
- Phase properties of optical linear amplifiers. John A. Vaccaro and D. T. Pegg. Phys. Rev. A 49, 4985 (1994)
- Rodney Loudon, Ottavia Jedrkiewicz, Stephen M. Barnett, and John Jeffers. Quantum limits on noise in dual input-output linear optical amplifiers and attenuators. Phys. Rev. A 67, 043803 (2003)
- C. Lamprecht and H. Ritsch. Theory of excess noise in unstable resonator lasers. Phys. Rev. A 67, 013805(2003)