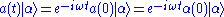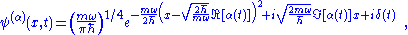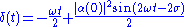Coherent state
Encyclopedia
In quantum mechanics
a coherent state is a specific kind of quantum state of the quantum harmonic oscillator
whose dynamics most closely resembles the oscillating behaviour of a classical harmonic oscillator. It was the first example of quantum dynamics when Erwin Schrödinger
derived it in 1926 while searching for solutions of the Schrödinger equation
that satisfy the correspondence principle
.
The quantum harmonic oscillator and hence, the coherent states, arises in the quantum theory of a wide range of physical systems
For instance, a coherent state describes the oscillating motion of the particle in a quadratic potential well (for an early reference, see e.g.
Schiff's textbook ).
These states, defined as eigenvectors of the lowering operator and forming an overcomplete family, were introduced in the early papers of John R. Klauder
, e.g.
.
In the quantum theory of light (quantum electrodynamics
) and other boson
ic quantum field theories
, coherent states were introduced by the work of Roy J. Glauber
in 1963. Here the coherent state of a field describes an oscillating field, the closest quantum state to a classical sinusoidal wave such as a continuous laser wave.
However, the concept of coherent states has been considerably generalized, to the extent that it has become a major topic in mathematical physics and in applied mathematics, with applications ranging from quantization
to signal processing
and image processing
(see Coherent states in mathematical physics
). For that reason, the coherent states associated to the quantum harmonic oscillator
are usually called
canonical coherent states (CCS) or standard coherent states or Gaussian states in the literature.
a coherent state is a specific kind of quantum state, applicable to the quantum harmonic oscillator
, the electromagnetic field, etc.
that describes a maximal kind of coherence and a classical kind of behavior. Erwin Schrödinger
derived it as a minimum uncertainty Gaussian wavepacket in 1926 while searching for solutions of the Schrödinger equation that satisfy the correspondence principle
. It is a minimum uncertainty state, with the single free parameter chosen to make the relative dispersion (standard deviation divided by the mean) equal for position and momentum, each being equally small at high energy.
Further, contrary to the energy eigenstates of the system, the time evolution of a coherent state is concentrated along the classical trajectories.
The quantum linear harmonic oscillator and hence, the coherent states, arise in the quantum theory of a wide range of physical systems. They are found in the quantum theory of light (quantum electrodynamics
) and other bosonic quantum field theories.
While minimum uncertainty Gaussian wave-packets were well-known, they did not attract much attention until Roy J. Glauber
, in 1963, provided a complete quantum-theoretic description of coherence in the electromagnetic field. In this respect, the concurrent contribution of E.C.G. Sudarshan should not be omitted, (there is, however, a note in Glauber's paper that reads: "Uses of these states as generating functions for the
-quantum states have, however, been made by J. Schwinger ).
Glauber was prompted to do this to provide a description of the Hanbury-Brown & Twiss experiment that generated very wide baseline (hundreds or thousands of miles) interference patterns that could be used to determine stellar diameters. This opened the door to a much more comprehensive understanding of coherence.
(For more, see Quantum mechanical description.)
In classical optics
light is thought of as electromagnetic waves radiating from a source. Often, coherent laser light is thought of as light that is emitted by many such sources that are in phase
. Actually, the picture of one photon being in-phase with another is not valid in quantum theory. Laser radiation is produced in a resonant cavity where the resonant frequency of the cavity is the same as the frequency associated with the atomic transitions providing energy flow into the field. As energy in the resonant mode builds up, the probability for stimulated emission, in that mode only, increases. That is a positive feedback loop in which the amplitude in the resonant mode increases exponentially until some non-linear effects limit it. As a counter-example, a light bulb radiates light into a continuum of modes, and there is nothing that selects any one mode over the other. The emission process is highly random in space and time (see thermal light). In a laser
, however, light is emitted into a resonant mode, and that mode is highly coherent
. Thus, laser light is idealized as a coherent state. (Classically we describe such a state by an electric field oscillating as a stable wave. See Fig.1)
The energy eigenstates of the linear harmonic oscillator (e.g., masses on springs, lattice vibrations in a solid, vibrational motions of nuclei in molecules, or oscillations in the electromagnetic field) are fixed-number quantum states. The Fock state
(e.g. a single photon) is the most particle-like state; it has a fixed number of particles, and phase is indeterminate. A coherent state distributes its quantum-mechanical uncertainty equally between the canonically conjugate coordinates, position and momentum, and the relative uncertainty in phase [defined heuristically] and amplitude are roughly equal—and small at high amplitude.
is defined to be the right eigenstate of the annihilation operator 
. Formally, this reads:
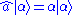
Since
is not hermitian, 
is a complex number that is not necessarily real, and can be represented as
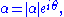
where
is a real number. Here 
and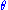 
are called the amplitude and phase of the state, respectively. The state 
is called a canonical coherent state in the literature, since there are many other types of coherent states, as can be seen in the companion article Coherent states in mathematical physics
.
Physically, this formula means that a coherent state is left unchanged by the detection (or annihilation) of field excitation or, say, a particle. The eigenstate of the annihilation operator has a Poissonian number distribution (as shown below). A Poisson distribution
is a necessary and sufficient condition that all detections are statistically independent. Compare this to a single-particle state (
Fock state
): once one particle is detected, there is zero probability of detecting another.
The derivation of this will make use of dimensionless operators,
and 
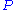, usually called field quadratures in quantum optics. These operators are related to the position and momentum of a mass 
on a spring with constant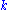 
:
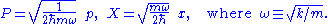
For an optical field
,
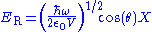
and
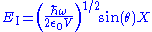
are the real and imaginary components of the mode of the electric field.
With these (dimensionless!) operators, the Hamiltonian of either system becomes
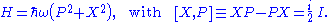
Erwin Schrödinger
was searching for the most classical-like states when he first introduced minimum uncertainty Gaussian wave-packets. The quantum state of the harmonic oscillator that minimizes the uncertainty relation with uncertainty equally distributed between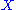
and 
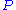satisfies the equation
.
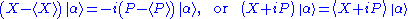It is an eigenstate of the operator
. (If the uncertainty is not balanced between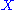 
and
, the state is now called a squeezed coherent state.)
Schrödinger found minimum uncertainty states for the linear harmonic oscillator to be the eigenstates of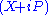
, and using the notation for multi-photon states, Glauber found the state of complete coherence to all orders in the electromagnetic field to be the right eigenstate of the annihilation operator—formally, in a mathematical sense, the same state. The name coherent state took hold after Glauber's work.
The coherent state's location in the complex plane (phase space
) is centered at the position and momentum of a classical oscillator of the same phase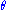
and amplitude (or the same complex electric field value for an electromagnetic wave). As shown in Figure 5, the uncertainty, equally spread in all directions, is represented by a disk with diameter 1/2. As the phase increases the coherent state circles the origin and the disk neither distorts nor spreads. This is the most similar a quantum state can be to a single point in phase space.
Since the uncertainty (and hence measurement noise) stays constant at 1/2 as the amplitude of the oscillation increases, the state behaves more and more like a sinusoidal wave, as shown in Figure 1. And, since the vacuum state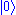
is just the coherent state with 
, all coherent states have the same uncertainty
as the vacuum. Therefore one can interpret the quantum noise of a coherent state as being due to the vacuum fluctuations.
The notation
does not refer to a Fock state
. For example, at
, one should not mistake 
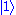
as a single-photon Fock state—it represents a Poisson distribution of fixed number states with a mean photon number of unity.
The formal solution of the eigenvalue equation is the vacuum state displaced to a location
in phase space, i.e., it is obtained by letting the unitary displacement operator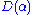 
operate on the vacuum:
,
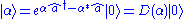where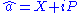
and 
.
This can be easily seen, as can virtually all results involving coherent states, using the representation of the coherent state in the basis of Fock states:
.
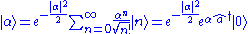where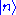
are energy (number) eigenvectors of the Hamiltonian 
. For the corresponding Poissonian distribution, the probability of detecting 
photons is:
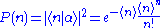
Similarly, the average photon number in a coherent state is
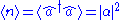
and the variance is
.
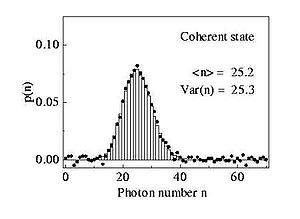
In the limit of large α these detection statistics are equivalent to that of a classical stable wave for all (large) values of 
.
These results apply to detection results at a single detector and thus relate to first order coherence (see degree of coherence). However, for measurements correlating detections at multiple detectors, higher-order coherence is involved (e.g., intensity correlations, second order coherence, at two detectors). Glauber's definition of quantum coherence involves nth-order correlation functions (n-th order coherence) for all n. The perfect coherent state has all n-orders of correlation equal to 1 (coherent). It is perfectly coherent to all orders.
Roy J. Glauber
's work was prompted by the results of Hanbury-Brown and Twiss that produced long-range (hundreds or thousands of miles) first-order interference patterns through the use of intensity fluctuations (lack of second order coherence), with narrow band filters (partial first order coherence) at each detector. (One can imagine, over very short durations, a near-instantaneous interference pattern from the two detectors, due to the narrow band filters, that dances around randomly due to the shifting relative phase difference. With a coincidence counter, the dancing interference pattern would be stronger at times of increased intensity [common to both beams], and that pattern would be stronger than the background noise.) Almost all of optics had been concerned with first order coherence. The Hanbury-Brown and Twiss results prompted Glauber to look at higher order coherence, and he came up with a complete quantum-theoretic description of coherence to all orders in the electromagnetic field (and a quantum-theoretic description of signal-plus-noise). He coined the term coherent state and showed that they are produced when a classical electrical current interacts with the electromagnetic field.
At
,
from Figure 5, simple geometry gives
.
From this we can see that there is a tradeoff between number uncertainty and phase uncertainty
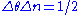, which sometimes can be interpreted as
the number-phase uncertainty relation. This is not a formal uncertainty relation: there is no uniquely defined phase operator in quantum mechanics
for the coherent state
. Now we have that
So the coherent state is an eigenstate of the annihilation operator in the Heisenberg picture. It is easy to show that in the Schrödinger picture the same eigenvalue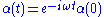
occurs:
Taking the coordinate representations we obtain the following differential equation
which is easily solved to give
where
is a still undetermined phase, which we must fix by demanding that the wavefunction satisfies the Schrödinger equation. We obtain that
where
is the initial phase of the eigenvalue, i.e. 
.
The mean position and momentum of the wavepacket
are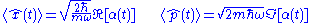
, namely,
Each of these properties may lead to generalizations, in general different from each other (see the article 'Coherent states in mathematical physics
' for some of these). We emphasize that
coherent states have mathematical features that are very different from those
of a Fock state
; for instance two different coherent states are not orthogonal:
(this is related to the fact that they are eigenvectors of the non-self-adjoint operator
).
Thus, if the oscillator is in the quantum state
it is also with nonzero probability in the other quantum state
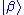(but the farther apart the states are situated in phase space, the lower the probability is). However, since they obey a closure relation, any state can be decomposed on the set of coherent states. They hence form an overcomplete basis in which one can diagonally decompose any state. This is the premise for the Sudarshan-Glauber P representation
. This closure relation can be expressed by the resolution of the identity operator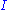
in the vector space of quantum states:
.
Another difficulty is that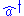
has no eigenket (and 
has no eigenbra). The following formal equality is the closest substitute and turns out to be very useful for technical computations:
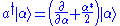
The last state is known as Agarwal state or photon-added coherent state and
denoted as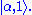
Normalized Agarwal states for order 
can be expressed as
The resolution of the identity may be derived (restricting to one spatial dimension for simplicity) by taking matrix elements between eigenstates of position,
, on both sides of the equation. On the right-hand side, this immediately gives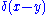 
. On the left-hand side, the same is obtained by inserting
from the previous section (time is arbitrary), then integrating over
using the Fourier representation of the delta function, and then performing a Gaussian integral
over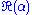
.
The resolution of the identity may also be expressed in terms of particle position and momentum.
For each coordinate dimension, using an adapted notation with new meaning of
,
the closure relation of coherent states reads
This can be inserted in any quantum-mechanical expectation value, relating it to some
quasi-classical phase-space integral and explaining, in particular, the origin of
normalisation factors
for classical
partition functions
consistent with quantum
mechanics.
In addition to being an exact eigenstate of annihilation operators, a coherent state is
an approximate common eigenstate of particle position and momentum. Restricting to
one dimension again,
The error in these approximations is measured by the uncertainties
of position and momentum,
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
a coherent state is a specific kind of quantum state of the quantum harmonic oscillator
Quantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
whose dynamics most closely resembles the oscillating behaviour of a classical harmonic oscillator. It was the first example of quantum dynamics when Erwin Schrödinger
Erwin Schrödinger
Erwin Rudolf Josef Alexander Schrödinger was an Austrian physicist and theoretical biologist who was one of the fathers of quantum mechanics, and is famed for a number of important contributions to physics, especially the Schrödinger equation, for which he received the Nobel Prize in Physics in 1933...
derived it in 1926 while searching for solutions of the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
that satisfy the correspondence principle
Correspondence principle
In physics, the correspondence principle states that the behavior of systems described by the theory of quantum mechanics reproduces classical physics in the limit of large quantum numbers....
.
The quantum harmonic oscillator and hence, the coherent states, arises in the quantum theory of a wide range of physical systems
For instance, a coherent state describes the oscillating motion of the particle in a quadratic potential well (for an early reference, see e.g.
Schiff's textbook ).
These states, defined as eigenvectors of the lowering operator and forming an overcomplete family, were introduced in the early papers of John R. Klauder
John R. Klauder
John R. Klauder is an American professor of physics and mathematics and author of over 250 published articles on physics....
, e.g.
.
In the quantum theory of light (quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
) and other boson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
ic quantum field theories
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, coherent states were introduced by the work of Roy J. Glauber
Roy J. Glauber
Roy Jay Glauber is an American theoretical physicist. He is the Mallinckrodt Professor of Physics at Harvard University and Adjunct Professor of Optical Sciences at the University of Arizona...
in 1963. Here the coherent state of a field describes an oscillating field, the closest quantum state to a classical sinusoidal wave such as a continuous laser wave.
However, the concept of coherent states has been considerably generalized, to the extent that it has become a major topic in mathematical physics and in applied mathematics, with applications ranging from quantization
Quantization
Quantization is the procedure of constraining something from a relatively large or continuous set of values to a relatively small discrete set...
to signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
and image processing
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
(see Coherent states in mathematical physics
Coherent states in mathematical physics
Coherent states have been introduced in a physical context, first as quasi-classical states in quantum mechanics, then as the backbone of quantum optics and they are described in that spirit in the articleCoherent states ....
). For that reason, the coherent states associated to the quantum harmonic oscillator
Quantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
are usually called
canonical coherent states (CCS) or standard coherent states or Gaussian states in the literature.
Coherent states in quantum optics
In quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
a coherent state is a specific kind of quantum state, applicable to the quantum harmonic oscillator
Quantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
, the electromagnetic field, etc.
that describes a maximal kind of coherence and a classical kind of behavior. Erwin Schrödinger
Erwin Schrödinger
Erwin Rudolf Josef Alexander Schrödinger was an Austrian physicist and theoretical biologist who was one of the fathers of quantum mechanics, and is famed for a number of important contributions to physics, especially the Schrödinger equation, for which he received the Nobel Prize in Physics in 1933...
derived it as a minimum uncertainty Gaussian wavepacket in 1926 while searching for solutions of the Schrödinger equation that satisfy the correspondence principle
Correspondence principle
In physics, the correspondence principle states that the behavior of systems described by the theory of quantum mechanics reproduces classical physics in the limit of large quantum numbers....
. It is a minimum uncertainty state, with the single free parameter chosen to make the relative dispersion (standard deviation divided by the mean) equal for position and momentum, each being equally small at high energy.
Further, contrary to the energy eigenstates of the system, the time evolution of a coherent state is concentrated along the classical trajectories.
The quantum linear harmonic oscillator and hence, the coherent states, arise in the quantum theory of a wide range of physical systems. They are found in the quantum theory of light (quantum electrodynamics
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
) and other bosonic quantum field theories.
While minimum uncertainty Gaussian wave-packets were well-known, they did not attract much attention until Roy J. Glauber
Roy J. Glauber
Roy Jay Glauber is an American theoretical physicist. He is the Mallinckrodt Professor of Physics at Harvard University and Adjunct Professor of Optical Sciences at the University of Arizona...
, in 1963, provided a complete quantum-theoretic description of coherence in the electromagnetic field. In this respect, the concurrent contribution of E.C.G. Sudarshan should not be omitted, (there is, however, a note in Glauber's paper that reads: "Uses of these states as generating functions for the
-quantum states have, however, been made by J. Schwinger ).Glauber was prompted to do this to provide a description of the Hanbury-Brown & Twiss experiment that generated very wide baseline (hundreds or thousands of miles) interference patterns that could be used to determine stellar diameters. This opened the door to a much more comprehensive understanding of coherence.
(For more, see Quantum mechanical description.)
In classical optics
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
light is thought of as electromagnetic waves radiating from a source. Often, coherent laser light is thought of as light that is emitted by many such sources that are in phase
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
. Actually, the picture of one photon being in-phase with another is not valid in quantum theory. Laser radiation is produced in a resonant cavity where the resonant frequency of the cavity is the same as the frequency associated with the atomic transitions providing energy flow into the field. As energy in the resonant mode builds up, the probability for stimulated emission, in that mode only, increases. That is a positive feedback loop in which the amplitude in the resonant mode increases exponentially until some non-linear effects limit it. As a counter-example, a light bulb radiates light into a continuum of modes, and there is nothing that selects any one mode over the other. The emission process is highly random in space and time (see thermal light). In a laser
Laser
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of photons. The term "laser" originated as an acronym for Light Amplification by Stimulated Emission of Radiation...
, however, light is emitted into a resonant mode, and that mode is highly coherent
Coherence (physics)
In physics, coherence is a property of waves that enables stationary interference. More generally, coherence describes all properties of the correlation between physical quantities of a wave....
. Thus, laser light is idealized as a coherent state. (Classically we describe such a state by an electric field oscillating as a stable wave. See Fig.1)
The energy eigenstates of the linear harmonic oscillator (e.g., masses on springs, lattice vibrations in a solid, vibrational motions of nuclei in molecules, or oscillations in the electromagnetic field) are fixed-number quantum states. The Fock state
Fock state
A Fock state , in quantum mechanics, is any element of a Fock space with a well-defined number of particles . These states are named after the Soviet physicist, V. A. Fock.-Definition:...
(e.g. a single photon) is the most particle-like state; it has a fixed number of particles, and phase is indeterminate. A coherent state distributes its quantum-mechanical uncertainty equally between the canonically conjugate coordinates, position and momentum, and the relative uncertainty in phase [defined heuristically] and amplitude are roughly equal—and small at high amplitude.
Quantum mechanical definition
Mathematically, the coherent state is defined to be the right eigenstate of the annihilation operator . Formally, this reads: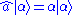Since
is not hermitian, is a complex number that is not necessarily real, and can be represented as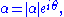where
is a real number. Here and 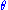are called the amplitude and phase of the state, respectively. The state is called a canonical coherent state in the literature, since there are many other types of coherent states, as can be seen in the companion article Coherent states in mathematical physicsCoherent states in mathematical physics
Coherent states have been introduced in a physical context, first as quasi-classical states in quantum mechanics, then as the backbone of quantum optics and they are described in that spirit in the articleCoherent states ....
.
Physically, this formula means that a coherent state is left unchanged by the detection (or annihilation) of field excitation or, say, a particle. The eigenstate of the annihilation operator has a Poissonian number distribution (as shown below). A Poisson distribution
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
is a necessary and sufficient condition that all detections are statistically independent. Compare this to a single-particle state (
Fock stateFock state
A Fock state , in quantum mechanics, is any element of a Fock space with a well-defined number of particles . These states are named after the Soviet physicist, V. A. Fock.-Definition:...
): once one particle is detected, there is zero probability of detecting another.
The derivation of this will make use of dimensionless operators,
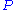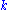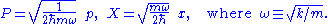
and , usually called field quadratures in quantum optics. These operators are related to the position and momentum of a mass on a spring with constant :For an optical field
Optical field
The optical field is a term used in physics and vector calculus to designate the electric field shown as E in the electromagnetic wave equation which can be derived from Maxwell's Equations...
,
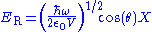
and
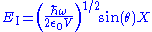
are the real and imaginary components of the mode of the electric field.
With these (dimensionless!) operators, the Hamiltonian of either system becomes
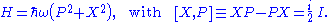
Erwin Schrödinger
Erwin Schrödinger
Erwin Rudolf Josef Alexander Schrödinger was an Austrian physicist and theoretical biologist who was one of the fathers of quantum mechanics, and is famed for a number of important contributions to physics, especially the Schrödinger equation, for which he received the Nobel Prize in Physics in 1933...
was searching for the most classical-like states when he first introduced minimum uncertainty Gaussian wave-packets. The quantum state of the harmonic oscillator that minimizes the uncertainty relation with uncertainty equally distributed between
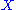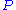and satisfies the equation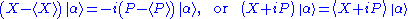.It is an eigenstate of the operator
. (If the uncertainty is not balanced between 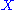and, the state is now called a squeezed coherent state.)Schrödinger found minimum uncertainty states for the linear harmonic oscillator to be the eigenstates of
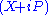, and using the notation for multi-photon states, Glauber found the state of complete coherence to all orders in the electromagnetic field to be the right eigenstate of the annihilation operator—formally, in a mathematical sense, the same state. The name coherent state took hold after Glauber's work.The coherent state's location in the complex plane (phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
) is centered at the position and momentum of a classical oscillator of the same phase
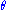and amplitude (or the same complex electric field value for an electromagnetic wave). As shown in Figure 5, the uncertainty, equally spread in all directions, is represented by a disk with diameter 1/2. As the phase increases the coherent state circles the origin and the disk neither distorts nor spreads. This is the most similar a quantum state can be to a single point in phase space.Since the uncertainty (and hence measurement noise) stays constant at 1/2 as the amplitude of the oscillation increases, the state behaves more and more like a sinusoidal wave, as shown in Figure 1. And, since the vacuum state
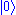is just the coherent state with , all coherent states have the same uncertaintyas the vacuum. Therefore one can interpret the quantum noise of a coherent state as being due to the vacuum fluctuations.
The notation
does not refer to a Fock stateFock state
A Fock state , in quantum mechanics, is any element of a Fock space with a well-defined number of particles . These states are named after the Soviet physicist, V. A. Fock.-Definition:...
. For example, at
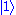
, one should not mistake as a single-photon Fock state—it represents a Poisson distribution of fixed number states with a mean photon number of unity.
The formal solution of the eigenvalue equation is the vacuum state displaced to a location
in phase space, i.e., it is obtained by letting the unitary displacement operator 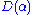operate on the vacuum: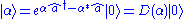,where
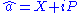and .This can be easily seen, as can virtually all results involving coherent states, using the representation of the coherent state in the basis of Fock states:
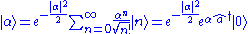.where
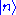are energy (number) eigenvectors of the Hamiltonian . For the corresponding Poissonian distribution, the probability of detecting photons is: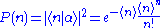Similarly, the average photon number in a coherent state is
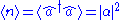
and the variance is
..These results apply to detection results at a single detector and thus relate to first order coherence (see degree of coherence). However, for measurements correlating detections at multiple detectors, higher-order coherence is involved (e.g., intensity correlations, second order coherence, at two detectors). Glauber's definition of quantum coherence involves nth-order correlation functions (n-th order coherence) for all n. The perfect coherent state has all n-orders of correlation equal to 1 (coherent). It is perfectly coherent to all orders.
Roy J. Glauber
Roy J. Glauber
Roy Jay Glauber is an American theoretical physicist. He is the Mallinckrodt Professor of Physics at Harvard University and Adjunct Professor of Optical Sciences at the University of Arizona...
's work was prompted by the results of Hanbury-Brown and Twiss that produced long-range (hundreds or thousands of miles) first-order interference patterns through the use of intensity fluctuations (lack of second order coherence), with narrow band filters (partial first order coherence) at each detector. (One can imagine, over very short durations, a near-instantaneous interference pattern from the two detectors, due to the narrow band filters, that dances around randomly due to the shifting relative phase difference. With a coincidence counter, the dancing interference pattern would be stronger at times of increased intensity [common to both beams], and that pattern would be stronger than the background noise.) Almost all of optics had been concerned with first order coherence. The Hanbury-Brown and Twiss results prompted Glauber to look at higher order coherence, and he came up with a complete quantum-theoretic description of coherence to all orders in the electromagnetic field (and a quantum-theoretic description of signal-plus-noise). He coined the term coherent state and showed that they are produced when a classical electrical current interacts with the electromagnetic field.
At
,from Figure 5, simple geometry gives
.From this we can see that there is a tradeoff between number uncertainty and phase uncertainty
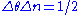, which sometimes can be interpreted asthe number-phase uncertainty relation. This is not a formal uncertainty relation: there is no uniquely defined phase operator in quantum mechanics
The wavefunction of a coherent state
To find the wavefunction of the coherent state, it is easiest to employ the Heisenberg picture of the quantum harmonic oscillatorQuantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
for the coherent state
. Now we have that
So the coherent state is an eigenstate of the annihilation operator in the Heisenberg picture. It is easy to show that in the Schrödinger picture the same eigenvalue
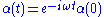occurs:-
.
Taking the coordinate representations we obtain the following differential equation
which is easily solved to give
where
is a still undetermined phase, which we must fix by demanding that the wavefunction satisfies the Schrödinger equation. We obtain that
where
is the initial phase of the eigenvalue, i.e. .The mean position and momentum of the wavepacket
are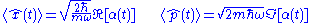Mathematical characteristics of the canonical coherent states
The canonical coherent states described so far have three properties that are mutually equivalent, since each of them completely specifies the state, namely,
- They are eigenvectors of the annihilation operator:
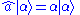. - They are obtained from the vacuum by application of a unitary displacement operator:
. - They are states of (balanced) minimal uncertainty:
.
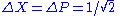Each of these properties may lead to generalizations, in general different from each other (see the article 'Coherent states in mathematical physics
Coherent states in mathematical physics
Coherent states have been introduced in a physical context, first as quasi-classical states in quantum mechanics, then as the backbone of quantum optics and they are described in that spirit in the articleCoherent states ....
' for some of these). We emphasize that
coherent states have mathematical features that are very different from those
of a Fock state
Fock state
A Fock state , in quantum mechanics, is any element of a Fock space with a well-defined number of particles . These states are named after the Soviet physicist, V. A. Fock.-Definition:...
; for instance two different coherent states are not orthogonal:
(this is related to the fact that they are eigenvectors of the non-self-adjoint operator
).Thus, if the oscillator is in the quantum state
it is also with nonzero probability in the other quantum state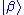 (but the farther apart the states are situated in phase space, the lower the probability is). However, since they obey a closure relation, any state can be decomposed on the set of coherent states. They hence form an overcomplete basis in which one can diagonally decompose any state. This is the premise for the Sudarshan-Glauber P representationGlauber P representation
The Glauber-Sudarshan P-representation is a way of writing down the state of any type of light using the coherent states as a basis. It was developed by George Sudarshan and later adopted by Roy J. Glauber...
. This closure relation can be expressed by the resolution of the identity operator
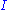in the vector space of quantum states:.Another difficulty is that
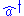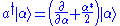
has no eigenket (and has no eigenbra). The following formal equality is the closest substitute and turns out to be very useful for technical computations:The last state is known as Agarwal state or photon-added coherent state and
denoted as
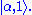Normalized Agarwal states for order can be expressed asThe resolution of the identity may be derived (restricting to one spatial dimension for simplicity) by taking matrix elements between eigenstates of position,
, on both sides of the equation. On the right-hand side, this immediately gives 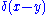. On the left-hand side, the same is obtained by insertingfrom the previous section (time is arbitrary), then integrating over
using the Fourier representation of the delta function, and then performing a Gaussian integralGaussian integral
The Gaussian integral, also known as the Euler-Poisson integral or Poisson integral, is the integral of the Gaussian function e−x2 over the entire real line.It is named after the German mathematician and...
over
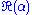.The resolution of the identity may also be expressed in terms of particle position and momentum.
For each coordinate dimension, using an adapted notation with new meaning of
,the closure relation of coherent states reads
This can be inserted in any quantum-mechanical expectation value, relating it to some
quasi-classical phase-space integral and explaining, in particular, the origin of
normalisation factors
for classicalpartition functions
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
consistent with quantum
mechanics.
In addition to being an exact eigenstate of annihilation operators, a coherent state is
an approximate common eigenstate of particle position and momentum. Restricting to
one dimension again,
The error in these approximations is measured by the uncertainties
Uncertainty principle
In quantum mechanics, the Heisenberg uncertainty principle states a fundamental limit on the accuracy with which certain pairs of physical properties of a particle, such as position and momentum, can be simultaneously known...
of position and momentum,
Coherent states of Bose–Einstein condensates
- A Bose–Einstein condensateBose–Einstein condensateA Bose–Einstein condensate is a state of matter of a dilute gas of weakly interacting bosons confined in an external potential and cooled to temperatures very near absolute zero . Under such conditions, a large fraction of the bosons occupy the lowest quantum state of the external potential, at...
(BEC) is a collection of boson atoms that are all in the same quantum state. In a thermodynamic system, the ground state becomes macroscopically occupied below a critical temperature — roughly when the thermal de Broglie wavelength is longer than the interatomic spacing. Superfluidity in liquid Helium-4 is believed to be associated with the Bose–Einstein condensation in an ideal gas. But 4He has strong interactions, and the liquid structure factor (a 2nd-order statistic) plays an important role. The use of a coherent state to represent the superfluid component of 4He provided a good estimate of the condensate / non-condensate fractions in superfluidity,consistent with results of slow neutron scattering. Most of the special superfluid properties follow directly from the use of a coherent state to represent the superfluid component — that acts as a macroscopically occupied single-body state with well-defined amplitude and phase over the entire volume. (The superfluid component of 4He goes from zero at the transition temperature to 100% at absolute zero. But the condensate fraction is about 6% at absolute zero temperature, T=0° K.) - Early in the study of superfluidity, Penrose and Onsager proposed a metric ("order parameter") for superfluidity. It was represented by a macroscopic factored component (a macroscopic eigenvalue) in the first-order reduced density matrix. Later, C. N. Yang proposed a more generalized measure of macroscopic quantum coherence, called "Off-Diagonal Long-Range Order" (ODLRO), that included fermion as well as boson systems. ODLRO exists whenever there is a macroscopically large factored component (eigenvalue) in a reduced density matrix of any order. Superfluidity corresponds to a large factored component in the first-order reduced density matrix. (And, all higher order reduced density matrices behaved similarly.) Superconductivity involves a large factored component in the 2nd-order ("Cooper electron-pairCooper pairIn condensed matter physics, a Cooper pair or BCS pair is two electrons that are bound together at low temperatures in a certain manner first described in 1956 by American physicist Leon Cooper...
") reduced density matrix. - The orders of reduced density matrices used to describe macroscopic quantum coherence in superfluids are formally the same as the correlation functions used to describe orders of coherence in radiation. Both are examples of macroscopic quantum coherence. The macroscopically large coherent component, plus noise, in the electromagnetic field, as given by Glauber's description of signal-plus-noise, is formally the same as the macroscopically large superfluid component plus normal fluid component in the two-fluid model of superfluidity.
- Every-day electromagnetic radiation, such as radio and TV waves, is also an example of near coherent states (macroscopic quantum coherence). That should "give one pause" regarding the conventional demarcation between quantum and classical.
Coherent electron states in superconductivity
- Electrons are fermions, but when they pair up into Cooper pairCooper pairIn condensed matter physics, a Cooper pair or BCS pair is two electrons that are bound together at low temperatures in a certain manner first described in 1956 by American physicist Leon Cooper...
s they act as bosons, and so can collectively form a coherent state at low temperatures. Such coherent states are part of the explanation of effects such as the Quantum Hall effect in low-temperature superconducting semiconductors.
Generalizations
- According to Gilmore and Perelomov, who showed it independently, the construction of coherent states may be seen as a problem in group theoryGroup theoryIn mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, and thus coherent states may be associated to groups different from the Heisenberg group, which leads to the canonical coherent states discussed above. Moreover, these coherent states may be generalized to quantum groups. These topics, with references to original work, are discussed in detail in Coherent states in mathematical physicsCoherent states in mathematical physicsCoherent states have been introduced in a physical context, first as quasi-classical states in quantum mechanics, then as the backbone of quantum optics and they are described in that spirit in the articleCoherent states ....
.
- In quantum field theoryQuantum field theoryQuantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
and string theoryString theoryString theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, a generalization of coherent states to the case of infinitely many degrees of freedomDegrees of freedom (physics and chemistry)A degree of freedom is an independent physical parameter, often called a dimension, in the formal description of the state of a physical system...
is used to define a vacuum stateVacuum stateIn quantum field theory, the vacuum state is the quantum state with the lowest possible energy. Generally, it contains no physical particles...
with a different vacuum expectation valueVacuum expectation valueIn quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
from the original vacuum.
- In one-dimensional many-body quantum systems with fermionic degrees of freedom, low energy excited states can be approximated as coherent states of a bosonic field operator that creates particle-hole excitations. This approach is called bosonizationBosonizationIn theoretical physics, one often studies two-dimensional conformal field theory. It has many very special properties. One of them is the equivalence of fermionic elementary fields and bosonic elementary fields. Bosonization also appears in 2D theories which aren't conformal field theories.The...
.
- The Gaussian coherent states of nonrelativistic quantum mechanics can be generalized to relativistic coherent states of Klein-Gordon and Dirac particles.
- Coherent states have also appeared in works on loop quantum gravityLoop quantum gravityLoop quantum gravity , also known as loop gravity and quantum geometry, is a proposed quantum theory of spacetime which attempts to reconcile the theories of quantum mechanics and general relativity...
or for the construction of (semi)classical canonical quantum general relativity. See, for instance, .
See also
- Coherent states in mathematical physicsCoherent states in mathematical physicsCoherent states have been introduced in a physical context, first as quasi-classical states in quantum mechanics, then as the backbone of quantum optics and they are described in that spirit in the articleCoherent states ....
- Quantum field theoryQuantum field theoryQuantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
- Quantum opticsQuantum opticsQuantum optics is a field of research in physics, dealing with the application of quantum mechanics to phenomena involving light and its interactions with matter.- History of quantum optics :...
- Electromagnetic fieldElectromagnetic fieldAn electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
- degree of coherence
- quantum amplifierQuantum amplifierA quantum amplifer is an amplifier that uses quantum mechanical methods to amplify a quantum signal; examples include the active elements of optical lasers and optical re-transmitters....