In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

 and applications, quantum annealing (QA) is a general method for finding the global minimum of a given objective function over a given set of candidate solutions (the search space), by a process analogous to quantum fluctuation

Quantum fluctuation

In quantum physics, a quantum fluctuation is the temporary change in the amount of energy in a point in space, arising from Werner Heisenberg's uncertainty principle.According to one formulation of the principle,energy and time can be related by the relation...

s. It is used mainly for problems where the search space is discrete (combinatorial optimization

Combinatorial optimization

In applied mathematics and theoretical computer science, combinatorial optimization is a topic that consists of finding an optimal object from a finite set of objects. In many such problems, exhaustive search is not feasible...

 problems) with many local minima; such as finding the ground state

Ground state

The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...

s of a glassy system.

In quantum annealing, a "current state" (the current candidate solution) is randomly replaced by a randomly selected neighbor state 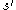if the latter has a lower "energy" (value of the objective function). The process is controlled by the "tunneling field strength" 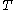, a parameter that determines the extent of the neighborhood of states explored by the method. The tunneling field starts high, so that the neighborhood extends over the whole search space; and is slowly reduced through the computation, until the neighborhood shrinks to those few states that differ minimally from the current states.

Comparison to simulated annealing

Quantum annealing can be compared to simulated annealing

Simulated annealing

Simulated annealing is a generic probabilistic metaheuristic for the global optimization problem of locating a good approximation to the global optimum of a given function in a large search space. It is often used when the search space is discrete...

 (SA), whose "temperature" parameter plays a similar role to QA's tunneling field strength. However, in SA the neighborhood stays the same throughout the search, and the temperature determines the probability of moving to a state of higher "energy". In QA, the tunneling field strength determines instead the neighborhood radius, i.e. the mean distance between the next candidate 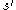and the current candidate .

In more elaborated SA variants (such as Adaptive simulated annealing

Adaptive simulated annealing

Adaptive simulated annealing is a variant of simulated annealing algorithm in which the algorithm parameters that control temperature schedule and random step selection are automatically adjusted according to algorithm progress. This makes the algorithm more efficient and less sensitive to user...

), the neighborhood radius is also varied using acceptance rate percentages or the temperature value.

Quantum mechanics analogy

The tunneling field is basically a kinetic energy term that does not commute with the classical potential energy part of the original glass. The whole process can be simulated in a computer using quantum Monte Carlo

Quantum Monte Carlo

Quantum Monte Carlo is a large class of computer algorithms that simulate quantum systems with the idea of solving the quantum many-body problem. They use, in one way or another, the Monte Carlo method to handle the many-dimensional integrals that arise...

 (or other stochastic technique), and thus obtain a heuristic algorithm for finding the ground state of the classical glass. It is speculated that in a quantum computer

Quantum computer

A quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from traditional computers based on transistors...

, such simulations would be much more efficient and exact than that done in a classical computer, due to quantum parallelism realized by the actual superposition of all the classical configurations at any instant.

By that time, the system finds a very deep (likely, the global one) minimum and settle there. At the end, we are left with the classical system at its global minimum.

In the case of annealing a purely mathematical objective function, one may consider the variables in the problem to be classical degrees of freedom, and the cost functions to be the potential energy function (classical Hamiltonian). Then a suitable term consisting of non-commuting variable(s) (i.e. variables that has non-zero commutator with the variables of the original mathematical problem) has to be introduced artificially in the Hamiltonian to play the role of the tunneling field (kinetic part). Then one may carry out the simulation with the quantum Hamiltonian thus constructed (the original function + non-commuting part) just as described above. Here, there is a choice in selecting the non-commuting term and the efficiency of annealing may depend on that.

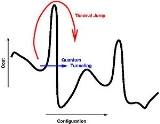
It has been demonstrated experimentally as well as theoretically, that quantum annealing can indeed outperform thermal annealing in certain cases, especially, where the potential energy (cost) landscape consists of very high but thin barriers surrounding shallow local minima. Since thermal transition probabilities (~; 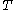=> Temperature, 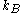=> Boltzmann constant) depend only on the height 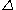of the barriers, it is very difficult for thermal fluctuations to get the system out from such local minima. But quantum tunneling probabilities through a barrier depend not only the height of the barrier, but also on its width 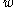; if the barriers are thin enough, quantum fluctuations may bring the system out of the shallow local minima surrounded by them.

Implementations

In 2011, D-Wave Systems

D-Wave Systems

D-Wave Systems, Inc. is a quantum computing company, based in Burnaby, British Columbia. On May 11, 2011, D-Wave System announced D-Wave One, labeled "the world's first commercially available quantum computer," and also referred to it as an adiabatic quantum computer using quantum annealing to...

 announced the first commercial quantum annealer on the market by the name D-Wave One. The company claims this system uses a 128 qubit processor chipset. On May 25, 2011 D-Wave announced that Lockheed Martin

Lockheed Martin

Lockheed Martin is an American global aerospace, defense, security, and advanced technology company with worldwide interests. It was formed by the merger of Lockheed Corporation with Martin Marietta in March 1995. It is headquartered in Bethesda, Maryland, in the Washington Metropolitan Area....

 Corporation entered into an agreement to purchase a D-Wave One system. On October 28, 2011 USC

University of Southern California

The University of Southern California is a private, not-for-profit, nonsectarian, research university located in Los Angeles, California, United States. USC was founded in 1880, making it California's oldest private research university...

's Information Sciences Institute

Information Sciences Institute

The Information Sciences Institute is a research and development unit of the University of Southern California's Viterbi School of Engineering which focuses on computer and communications technology and information processing...

took delivery of Lockheed's D-Wave One, where it has become the first operational commercial quantum computer.